Metoda kritické cesty (CPM - Critical Path Method)
Pro řešení metodou kritické cesty využíváme tzv. síťový graf,
který se skládá z uzlů a orientovaných hran. Hrany odpovídají jednotlivým
dílčím činnostem úkolu. Danou činnost jednoznačně určují počáteční a koncový
uzel, kterými je každá činnost ohraničena. Činnost označujeme uspořádanou
dvojici čísel (i, j), přičemž musí platit i < j, tj. v grafu se nevyskytují cykly a rovnoběžné hrany [Víteček, A., Wawrziczková, M.,
1988], [Vítečková, M.]).
Na realizaci činnosti je třeba určité doby, tzv. doby trvání činnosti tij, a vynaložení určitých nákladů.
Některé činnosti musí být vykonány v určitém časovém pořadí, proto je třeba do síťového grafu zavést ještě fiktivní činnosti (obr. 3.24 b) s nulovou dobou trvání, které vyjadřují vazby a závislosti mezi činnostmi.
Síťovým grafem G rozumíme tedy dvojici množin: množinu uzlů V a množinu činností E (množinu hran). Síťový graf zapisujeme ve tvaru G = (V, E).
a) b)
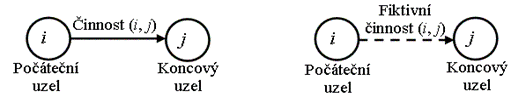
Obr. 3.24 Znázornění činnosti: a) skutečné, b) fiktivní
Posloupnost hran v síťovém grafu, u které koncový uzel každé hrany (mimo poslední) se shoduje s počátečním uzlem následující hrany, se nazývá cesta. Součet dob trvání všech činností tvořící cestu je doba trvání cesty.
Maximální doba trvání cesty z uzlu 1 do uzlu j se nazývá: nejdříve možný termín uzlu j,
označuje se symbolem 
a určí se ze vztahu:
.
Je to nejdříve možný termín zahájení všech činností vystupujících z uzlu j.
Termín realizace úkolu
je nejdříve možný
termín uzlu n. Je to minimální doba
nutná ke splnění všech činností a tím i celého úkolu. Této době odpovídá
maximální doba trvání cesty z uzlu 1 do uzlu n.
Symbolem 
se označuje nejpozději přípustný termín uzlu i. Je roven rozdílu mezi termínem 
. Předpokládá se, že nejdříve možný termín koncového uzlu
je zároveň roven
jeho nejpozději přípustnému termínu 
. Nejpozději přípustný termín vypočteme ze vztahu
Uzly, pro které platí:
,
nazýváme kritické uzly a činnosti, které spojují tyto kritické uzly nazýváme kritické činnosti a vytvářejí kritickou cestu v grafu. Dojde-li k jakémukoli zpoždění v provádění kritických činností, nutně dojde ke zpoždění splnění celého úkolu. V síťovém grafu může existovat několik kritických cest. Znalost kritických cest, a tedy i kritických činností, je pro řízení realizace celého úkolu velmi důležitá.
Časové rezervy
U každé operace rozeznáváme několik druhů časových rezerv (obr. 3.26):
Celková časová rezerva činnosti - představuje časový interval, ve kterém lze posunout celou dílčí akci, aniž by se tím ovlivnil výsledný plánovaný termín. Počítáme ji podle vztahu:
.
Volná časová rezerva je takový časový interval, o který lze prodloužit nebo posunout činnost, aniž by byla ovlivněna činnost na ni navazující. Tuto rezervu počítáme podle vztahu:
.
Nezávislá časová rezerv, je to množství času, o který může být činnost prodloužena, aniž by se tím ovlivnila kterákoliv jiná činnost síťového grafu. Výpočet se provede dle vztahu:
.
Mezi jednotlivými časovými rezervami platí vztah:
.
Kritické činnosti mají nulové celkové časové rezervy (
).
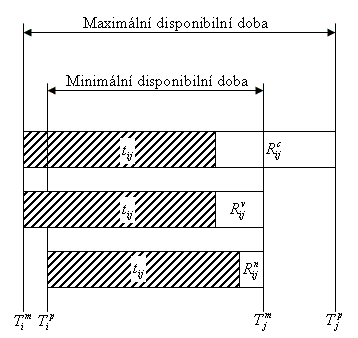
Obr. 3.26 Vzájemné vztahy mezi časovými rezervami
Subkritické činnosti jsou činnosti s malou celkovou časovou rezervou 
,
kde je:
δ - předem zvolená minimální rezerva (závisí na povaze realizovaného úkolu).
Síťový graf má tyto základní vlastnosti:
·
Každý síťový graf musí mít vždy jeden počátek,
ze kterého hrany pouze vystupují, a jeden konec, do kterého hrany pouze
vstupují. Tuto podmínku lze splnit vždy pomocí fiktivních činností (viz obr.
· Každá činnost může být zahájena jen tehdy, když jsou dokončeny všechny předcházející činnosti .
· Souběžné (paralelní) činnosti z důvodu jednoznačné identifikace musí být odděleny fiktivní činností (viz obr. 3.27 b).
· Délky hran neodpovídají dobám trvání činností.
· Uzly lze očíslovat tak, aby platila nerovnost i < j. V tomto případě v síťovém grafu nevystupují cykly (viz obr. 3.27 c).
Při sestavování síťových grafů je třeba provést rozbor činností a uvědomit si, které činnosti bezprostředně předcházejí každé činnosti, které činnosti za danou činností bezprostředně následují, které činnosti probíhají souběžně a které činnosti na sobě nezávisejí. Všechny údaje o činnostech zapisujeme do tabulky, na jejíž základě pak sestavíme vlastní síťový graf.
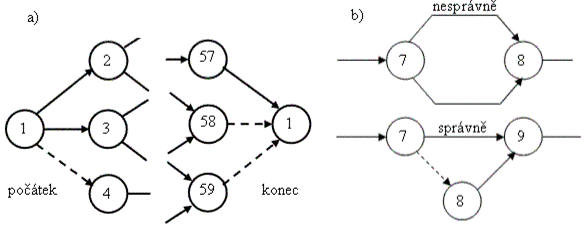
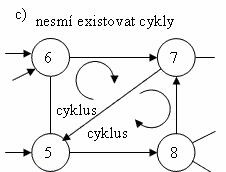
Obr. 3.27 Základní vlastnosti síťových grafů pro použití metody CPM
Pro očíslování uzlů v síťovém grafu můžeme použít následující algoritmus:
Očíslování uzlů síťového grafu:
· První krok - počátek označit číslem 1.
· Druhý krok - následujícím číslem označit libovolný neočíslovaný uzel, u kterého jsou všechny předcházející uzly očíslovány (takový uzel vždy existuje, protože síťový graf neobsahuje cykly). Krok 2 je třeba opakovat tak dlouho, až budou všechny uzly očíslovány. Konec bude mít vždy největší číslo rovné počtu uzlů.
Po očíslování uzlů můžeme kritickou cestu a časové rezervy určit algoritmem:
Určení nejdříve možných termínů (postup vpřed):
První krok -
položit 
.
Druhý krok - pro j = 2, 3, …, n vypočítat:
.
Určení nejpozději přípustných termínů uzlů (postup vzad):
Třetí krok - položit
, musí platit:
.
Čtvrtý krok - pro i = n – 1, n – 2, …, 1 vypočítat:
.
Určení časových rezerv činností:
Pátý krok - pro 
vypočítat:
,
kde je:
- nejdříve možný
termín uzlu j,
- nejpozději přípustný
termín uzlu j,
- doba trvání
činnosti.
Určení kritické cesty
Šestý krok -
vyznačit činnosti (i, j), pro které 
Tyto činnosti jsou
kritické a určují kritickou cestu.
U jednoduchých síťových grafů určení kritické cesty provádíme
přímo v síťovém grafu [Víteček, A., Wawrziczková, M., 1988]. Po očíslování uzlů postupujeme
nejdříve od počátku ke konci (postup vpřed) a počítáme všechny nejdříve možné
termíny a zapisujeme je vlevo (viz obr. 3.29). Pak postupujeme od konce
k počátku (postup vzad) a počítáme nejpozději přípustné termíny a
zapisujeme je vpravo. Kritickou cestu vyznačují uzly, u kterých nejdříve možné
termíny jsou shodné s nejpozději přípustnými termíny 
. Celkové časové rezervy zapisujeme u jednotlivých činností
do závorek (viz obr. 3.28). U kritických činností všechny časové
rezervy jsou nulové.
Agregace a desagregace síťových grafů
Každý síťový graf svojí strukturou odpovídá úrovni řízení, pro kterou je určen. Pro vyšší úrovně je méně podrobný – je agregován. Agregace se týká nejen činností, ale i dob jejich trvání. Při agregaci síťového grafu je třeba vyznačit důležité tzv. klíčové uzly, které v agregovaném síťovém grafu mají zůstat. Dobu trvání agregované činnosti určuje největší doba trvání cesty z jejího počátečního do jejího koncového uzlu. Mezi dvěma klíčovými uzly uvažujeme činnost tehdy, existuje-li mezi těmito uzly cesta ve výchozím síťovém grafu, respektive tvoří-li tato činnost cestu s nejdelší dobou trvání mezi těmito uzly.
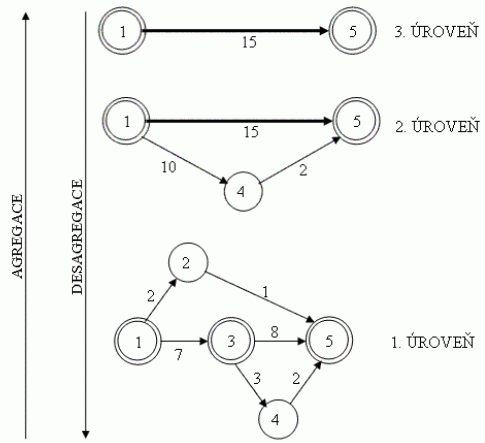
Obr. 3.30 Znázornění agregace a desagregace síťových grafů
Agregace a desagregace síťového grafu umožňuje použití metody kritické cesty s výhodou v hierarchické struktuře řízení. Je to také jeden z hlavních důvodů jejího využívání při plánování a řízení realizace složitých úkolů, především rozsáhlých projektů s počtem činností až do několika desetitisíců. Metoda kritické cesty je však s úspěchem používána i pro nevelké projekty, ve kterých vystupuje pouze několik desítek činností.
Zde jsou příklady na procvičení probrané látky. Metoda kritické cesty.