Příklad 3.6
Síťový graf G na obr. 3.25 popíšeme množinou uzlů V a množinou hran E.
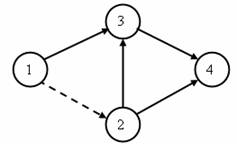
Obr. 3.25 Síťový graf k příkladu 3.6
Řešení:
Pro síťový graf podle obr. 3.25 platí G = (V, E),
kde je: V = [1, 2, 3, 4],
E = [(1; 2), (1; 3), (2; 3), (2; 4), (3; 4)].
Příklad 3.7
Máme za úkol sestrojit zařízení, které se skládá ze tří částí. Podle tabulky 3.5 sestrojte síťový graf a určete kritickou cestu a časové rezervy. Činnosti jsou označeny písmeny velké abecedy. Například symbol A < B, C označuje, že činnost A předchází činnostem B a C a tak dále. Doby trvání činností jsou uvedeny ve zvolených časových jednotkách (č.j.).
Tabulka 3.5 Vypočtené hodnoty k příkladu 3.7
|
činnost |
|
i |
j |
|
podmínky |
|
vstupní návrh |
A |
1 |
2 |
2 |
A < B, C |
|
fiktivní činnost |
B |
2 |
3 |
0 |
|
|
projekt |
C |
2 |
4 |
5 |
C < E, F, G |
|
rozbor |
D |
3 |
4 |
3 |
D < E, F, G |
|
objednávka 1 |
E |
4 |
5 |
1 |
E < H |
|
objednávka 2 |
F |
4 |
6 |
2 |
F < I |
|
objednávka 3 |
G |
4 |
7 |
1 |
G < J |
|
dodávka součástky 1 |
H |
5 |
8 |
3 |
H < K |
|
dodávka součástky 2 |
I |
6 |
8 |
3 |
I < K |
|
dodávka součástky 3 |
J |
7 |
9 |
4 |
J < L |
|
dílčí montáž |
K |
8 |
9 |
4 |
K < L |
|
konečná montáž |
L |
9 |
10 |
5 |
|
Řešení:
Nejdříve sestrojíme síťový graf s uvažováním omezení na časové činnosti, viz obr.3.28. Přečíslování uzlů nemusíme provádět, protože vyhovuje podmínce i < j.
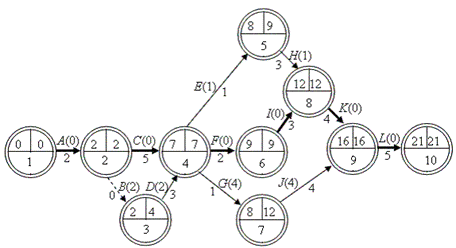
Obr. 3.28 Síťový graf k příkladu 3.7
V uzlech jsou hodnoty
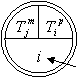číslo uzlu
Obr. 3.29 Označení uzlů na obr. 3.28
Výpočet nejdříve možných a nejpozději přípustných termínů provedeme přímo v síťovém grafu. Například nejdříve možný a nejpozději přípustný termín uzlu 4 je :
časových jednotek (i = 2, 3),
časových jednotek (j = 5, 6, 7),
pro jiné uzly je postup stejný.
Kritická cesta vede přes uzly: 1 – 2 – 4 – 6 – 8 – 9 – 10 (zesílenou čarou).
Doba realizace celého úkolu: 
= 
= 21 č. j.
Časové rezervy při výpočtu je vhodné sestavit do tabulky (viz
tabulka 3.6), protože fiktivní činnost (2,3) slouží pouze k jednoznačné
identifikaci činnosti (3, 4), dostaneme, že činnost (3,4) má nezávislou časovou
rezervu 2 č.j. Činnosti (4,5) a (5,8) mají celkovou
časovou rezervu 1 č. j. a činnosti (4,7) a (7,9) mají
celkovou časovou rezervu 4 č.j. Zvolíme-li 
č. j.,
dostaneme, že činnosti (4,5) a (5,8) lze považovat za subkritické
činnosti,
kde je:
- předem zvolená
minimální rezerva.
Tabulka 3.6 Časové rezervy k příkladu 3.7
|
|
i |
j |
|
|
|
|
|
A |
1 |
2 |
2 |
0 |
0 |
0 |
|
B |
2 |
3 |
0 |
2 |
0 |
0 |
|
C |
2 |
4 |
5 |
0 |
0 |
0 |
|
D |
3 |
4 |
3 |
2 |
2 |
2 |
|
E |
4 |
5 |
1 |
1 |
0 |
0 |
|
F |
4 |
6 |
2 |
0 |
0 |
0 |
|
G |
4 |
7 |
1 |
4 |
0 |
0 |
|
H |
5 |
8 |
3 |
1 |
1 |
0 |
|
I |
6 |
8 |
3 |
0 |
0 |
0 |
|
J |
7 |
9 |
4 |
4 |
4 |
0 |
|
K |
8 |
9 |
4 |
0 |
0 |
0 |
|
L |
9 |
10 |
5 |
0 |
0 |
0 |
