<<<< Obsah >>>>

Metoda minimální cesty

a) Orientovaný graf:

Pro určení minimální cesty v orientovaném ohodnoceném grafu se využívá Bellmanův princip optimality [Demel, J., 1988].

· je-li cesta z A do C optimální, pak na této cestě musí ležet i cesta z B do C

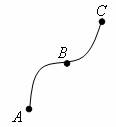
Obr. 3.17 Podmínka Bellmanova principu optimality

Podmínky pro graf, aby mohl být použít Bellmanův princip optimality:

· všechny hrany grafu jsou ohodnoceny ,

· v grafu nesmí být cykly Þ i < j (hrana musí vystupovat z uzlu i s číslem menším a vstupovat do uzlu j s číslem větším),

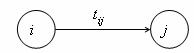
Obr. 3.18 Podmínka užití Bellmanova principu optimality

· nesmí být rovnoběžné hrany – odstraníme pomocí fiktivních hran s nulovým ohodnocením.

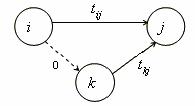
Obr. 3.19 Tvorba fiktivního prvku

Hrana spojující uzly i, k je fiktivní hrana s nulovým ohodnocením.

Postup určování cesty v orientovaném grafu:

Při hledání minimální (maximální) cesty v ohodnoceném orientovaném grafu postupujeme od koncového uzlu k počátečnímu uzlu.

Ohodnocení v koncovém uzlu (T_n = 0) položíme rovno nule. Pak postupujeme proti směru orientace hran k počátečnímu uzlu a u každého uzlu si pamatujeme minimální (maximální) hodnotu součtu ohodnocení hran předchozí části cesty a směr, odkud jsme do daného uzlu došli. Hodnota v počátečním uzlu dává celkovou nejkratší (nejdelší) cestu v grafu.

Tabulka 3.4 Stanovení délek cesty

Nejkratší cesta	Nejdelší cesta
Ti = min ( Tj + tij ) Tn = 0	Ti = max ( Tj + tij ) Tn = 0

Nejkratší cesta:

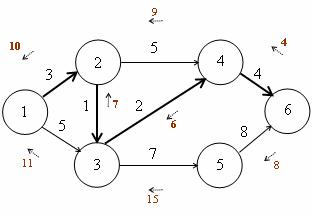
Obr. 3.20 Příklad orientovaného grafu – nejkratší cesta

Nejkratší cesta vede uzly: 1 – 2 – 3 – 4 – 6,

Délka cesty: 3 + 1 + 2 + 4 = 10 jednotek.

Nejdelší cesta:

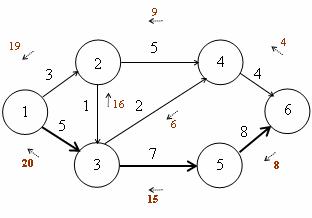
Obr. 3.21 Příklad orientovaného grafu – nejdelší cesta

Nejdelší cesta vede uzly: 1 – 3 – 5 – 6,

Délka cesty: 5 + 7 + 8 = 20 jednotek.

b) Neorientovaný graf

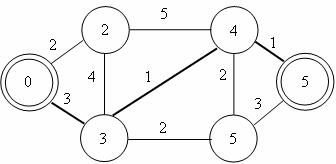
Obr. 3.22 Příklad neorientovaného grafu

Postup hledání minimální cesty v neorientovaném grafu:

Graf musí být ohodnocený, neorientovaný, bez číslování uzlů.

1. Označíme počáteční uzel číslem nula.

2. V každém dalším kroku budeme ohodnocovat neohodnocené uzly, které jsou spojeny hranami s již ohodnocenými uzly a to tak, že je hodnotíme podle vztahu

.

kde je: U( t_i ) - hodnota ohodnoceného uzlu,

t_ij - hodnota hrany mezi ohodnoceným a neohodnoceným uzlem.

3. Hodnota koncového uzlu nám dává hodnotu minimální cesty

4. Hrany, které leží na minimální cestě určíme podle vztahu

,

směrem od posledního uzlu k prvnímu.

Platí, že rozdíl hodnot sousedících uzlů musí být hodnota hrany.

a) b)

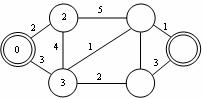
c) d)

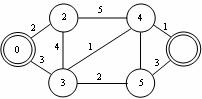
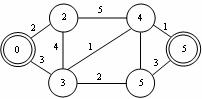
Obr. 3.23 Postup ohodnocování uzlů

<<<< Nahoru >>>>