Binomické rozdělení diskrétní náhodné veličiny
Předpokládejme, že určitý pokus opakujeme n-krát za stejných podmínek. V každém pokusu může nastat náhodný jev A (úspěch pokusu) se stejnou pravděpodobností p a nevyskytnout se (neúspěch pokusu) s pravděpodobností q = 1 – p [Kába, B., 1999].
Počet realizací náhodného jevu A (úspěchů) n nezávislých pokusů je zřejmě diskrétní náhodnou veličinou x, jež může nabývat hodnot 0, 1, …, n. Vzhledem k nezávislosti pokusů pro její frekvenční funkci platí:
![]() ,
,
kde je:
k = 0, 1, …, n.
Charakteristiky binomického rozdělení
Frekvenční funkci (pravděpodobnost, že k pokusů končí zdarem) binomického rozdělení diskrétní náhodné veličiny určíme podle vztahu

a distribuční funkci binomického rozdělení diskrétní náhodné veličiny určíme podle vztahu
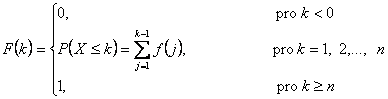 ,
,
kde je
n - počet nezávislých dílčích pokusů,
k - počet pokusů končících zdarem s pravděpodobností p,
(n-k)
- počet pokusů končících nezdarem s pravděpodobností q = 1 – p.
Číselné charakteristiky binomického rozdělení diskrétní náhodné veličiny
střední hodnota
![]() ,
,
rozptyl
![]() .
.
Zde jsou příklady na procvičení probrané látky. Binomické rozdělení diskrétní náhodné veličiny.