<<<< Obsah >>>>

Exponenciální rozdělení náhodné veličiny

Náhodnou veličinou je obvykle čas, v němž nastane sledovaný jev. Pravděpodobnost, že jev nastane v časovém okamžiku x. Používá se pro určování pravděpodobnosti, životnosti zařízení, pro řešení problémů teorie hromadné obsluhy a pro řešení teorie grafů [Kába, B., 1999].

Charakteristiky exponenciálního rozdělení

Hustotu pravděpodobnosti exponenciálního rozdělení náhodné veličiny (Obr. 2.19) určíme podle vztahu

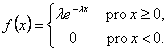
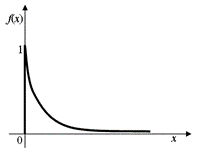
Obr. 2.19 Hustota pravděpodobnosti exponenciálního rozdělení

Distribuční funkci exponenciálního rozdělení náhodné veličiny (Obr. 2.20) určíme podle vztahu:

^.

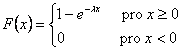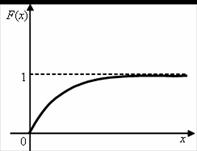
Obr. 2.20 Distribuční funkce exponenciálního rozdělení

Číselné charakteristiky exponenciálního rozložení:

střední hodnota

,

rozptyl

.

Pokud sledovaný jev může nastat až v čase a, kde a > 0, pak je hustota pravděpodobnosti:

distribuční funkce:

.

Grafy jsou posunuty. Rozptyl se nemění, střední hodnota je posunuta o hodnotu a (viz obr.2.21).

; .

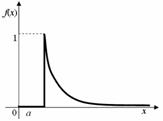
Obr. 2.21 Grafy hustoty pravděpodobnosti a distribuční funkce

exponenciálního rozdělení posunutého o hodnotu a

Zde jsou příklady na procvičení probrané látky. Exponenciální rozdělení náhodné veličiny.

<<<< Nahoru >>>>