<<<< Obsah >>>>

Normální rozdělení náhodné veličiny

a) Označováno též obecné normální rozdělení [Kába, B., 1999], [Škrášek, J., Tichý, Z., 1990], [Vítečková, M.]. Je velmi důležité, protože:

· se nejčastěji vyskytuje,

· mnoho jiných rozdělení se mu blíží,

· řada jiných rozdělení se jím dá nahradit.

Pravidlo 3s

Hodnoty náhodné veličiny jsou z intervalu		s pravděpodobností 0,6824.
Hodnoty náhodné veličiny jsou z intervalu		s pravděpodobností 0,9545.
Hodnoty náhodné veličiny jsou z intervalu		s pravděpodobností 0,9973.

Distribuční funkci normálního rozdělení náhodné veličiny určíme podle vztahu:

.

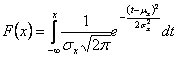Hustotu pravděpodobnosti normálního rozdělení náhodné veličiny určíme podle vztahu:

Obr. 2.16 Hustota pravděpodobnosti obecného normálního rozdělení

b) Normované normální rozdělení

Jedná se o speciální případ obecného normálního rozložení, kdy

kde je:

u - označení náhodné veličiny s normovaným normálním rozdělením.

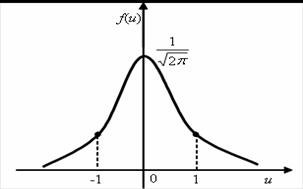
Obr. 2.17 Hustota pravděpodobnosti normovaného normálního rozdělení

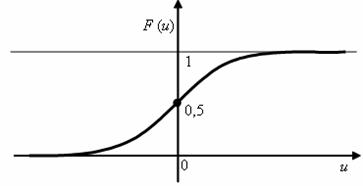
Obr. 2.18 Distribuční funkce normovaného normálního rozdělení

, .

Distribuční funkci normovaného normálního rozdělení náhodné veličiny určíme podle vztahu

,

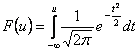a hustotu pravděpodobnosti normovaného normálního rozdělení náhodné veličiny určíme podle vztahu

.

Hodnoty distribuční funkce normovaného normálního rozdělení jsou uvedeny v  tabulce 2.7.

Transformace normovaného normálního rozdělení na obecné normální rozdělení

Pro transformaci platí vztah:

x_k = m_x + s_xu_k,

kde je:

u_k - hodnota náhodné veličiny normovaného normálního rozdělení,

x_k - vypočítané hodnoty obecného normálního rozdělení,

μ_x a s_x - střední hodnota a směrodatná odchylka obecného normálního rozdělení.

Opačná transformace se provádí podle vztahu:

.

Transformace rovnoměrného rozdělení na normální rozdělení

Tato transformace vychází z centrální limitní věty Linberga a Lévyho [Kába, B., 1999].

Věta:

Sečteme-li dostatečný počet hodnot náhodné veličiny x_i kde i = 1, 2, …, n, jež jsou vzájemně nezávislé a mají totéž rozdělení s toutéž střední hodnotou m_x a s tímtéž rozptylem , pak proměnná z vytvořená podle rovnice

,

s rostoucím n konverguje k normovanému normálnímu rozdělení

Pro transformaci normovaného rovnoměrného rozdělení na normované normální rozdělení je výhodné, aby n = 12, protože

pak

,

kde je:

r_i - hodnota náhodné veličiny normovaného rovnoměrného rozdělení,

u - hodnota náhodné veličiny normovaného normálního rozdělení.

Zde jsou příklady na procvičení probrané látky. Normální rozdělení náhodné veličiny.

<<<< Nahoru >>>>