Příklad 2.16

Ze zkušenosti je známo, že hmotnost určitých výrobků má normální rozdělení se směrodatnou odchylkou 1,1 g. Jaká je průměrná hmotnost těchto výrobků, jestliže pouze 3 % výrobků váží méně než 448 g?

Řešení:

Hmotnost výrobků je náhodnou veličinou X s rozdělením . Ze zadání úlohy vyplývá, že P(X < 448) = 0,03.

Pomocí vzorce:

dostaneme:

Z tabulky hodnot normální distribuční funkce ( tabulka 2.7) zjistíme, že

F(-1,88) = 0,03;

Hledaná průměrná hmotnost výrobku je .

Příklad 2.17

Hmotnost výrobku je vyhovující, pokud je v mezích 68 g až 69 g. Standardní hmotnost má obecné normální rozdělení se střední hodnotou m_x = 68,3 g a směrodatnou odchylkou s_x = 0,2 g. Jaká je pravděpodobnost, že hmotnost bude v mezích 68 g až 69 g?

Řešení:

Transformace na hodnoty normovaného normálního rozdělení:

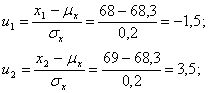
Protože hodnoty distribuční funkce jsou obvykle uváděny jen pro kladné hodnoty u, využije se vztahu:

F(1,5) + F(-1,5) = 1 Þ F(-1,5) = 1 - F(1,5) = 0,0668.

P(68 < x < 69) = P(-1,5 < x <3,5) = F(3,5) - F(-1,5) = 0,933.

Hmotnost bude ve stanovených mezích 68 g až 69 g s pravděpodobností 93,3 %. Byly použity hodnoty distribuční funkce normovaného normálního rozdělení z tabulky 2.7.

Příklad 2.18

Náhodná veličina x představující chybu měření má normální rozdělení se střední hodnotou m_x = 0,2 a rozptylem . Je třeba určit pravděpodobnost, že absolutní hodnota bude menší než jedna (|x| < 1).

Řešení:

N(0,2; 0,64), m_x = 0,2, .

Transformace na normální rovnoměrné rozdělení:

Z tabulky 2.7 jsou odečteny hodnoty distribuční funkce hodnot NV normovaného normálního rozdělení.

Absolutní hodnota x bude menší než jedna s pravděpodobností 77,4 %.