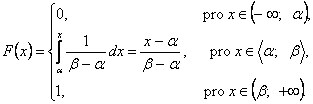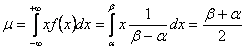<<<< Obsah >>>>

Rovnoměrné rozdělení náhodné veličiny

a) Obecné rovnoměrné rozdělení

Rovnoměrné rozdělení nabývají například chyby při zaokrouhlování čísel, chyby při odečítání údajů z lineárních měřicích přístrojů, doby čekání na uskutečnění jevu opakujícího se v pravidelných intervalech. Náhodná veličina X má rovnoměrné rozdělení, jestliže pro všechna x Î áa; bñ má konstantní hustotu pravděpodobnosti. Interval áa; bñ vymezuje hodnotu náhodné veličiny [Kába, B., 1999], [Vítečková, M.].

Tabulka 2.6: Charakteristiky rovnoměrného rozdělení

Hustota pravděpodobnosti:
Distribuční funkce:
Číselné charakteristiky
Střední hodnota:	Rozptyl:

Obr. 2.12 Hustota pravděpodobnosti

Obr. 2.13 Distribuční funkce

b) Normované rovnoměrné rozdělení

Při normovaném normálním rozdělení nabývá spojitá náhodná veličina hodnot z intervalu á0, 1ñ, a = 0, β = 1, z toho vyplývají hodnoty číselných charakteristik:

střední hodnota

,

rozptyl

.

Hustota pravděpodobnosti:

.

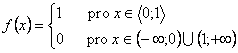Obr. 2.14 Hustota pravděpodobnosti normovaného rovnoměrného rozdělení

Distribuční funkce:

.

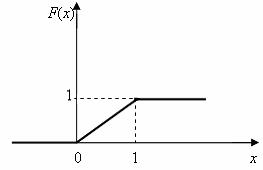
Obr. 2.15 Distribuční funkce normovaného rovnoměrného rozdělení

Transformace normovaného rovnoměrného rozdělení na obecné rovnoměrné rozdělení:

obecné

normované

kde jsou:

r_k - hodnoty normovaného rovnoměrného rozdělení,

x_k - hodnoty obecného rovnoměrného rozdělení se střední hodnotou m_x, a směrodatnou odchylkou .

Zde jsou příklady na procvičení probrané látky. Rovnoměrné rozložení náhodné veličiny.

<<<< Nahoru >>>>