8. Syntéza jednorozměrových diskrétních regulačních obvodů
Syntézou regulačního obvodu rozumíme návrh struktury regulátoru a jeho parametrů tak, aby byla dosažena požadovaná kvalita regulačního pochodu.
8.1 Malá, střední a velká vzorkovací perioda
Při analýze a syntéze (návrhu regulátoru) diskrétních regulačních obvodů vycházíme ze tří přístupů dle velikosti vzorkovací periody.
a) Pro malé vzorkovací periody T
Jak z názvu vyplývá tento přístup je možno uvažovat při malé vzorkovací periodě, převodník bereme jako součást regulátoru.
Malou vzorkovací periodu T můžeme definovat dle vztahů [Balátě, 2003]:
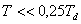 |
(8.1) |
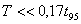 |
(8.2) |
-
kde
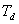 – dopravní zpoždění regulované soustavy,
– dopravní zpoždění regulované soustavy,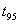 – doba, za kterou přechodová charakteristika regulované soustavy dosáhne 95 % ustálené hodnoty.
– doba, za kterou přechodová charakteristika regulované soustavy dosáhne 95 % ustálené hodnoty.
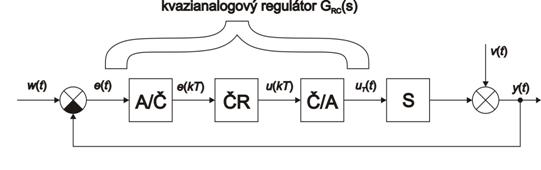
Tento přístup je velice častý a je užívám v 80% případů, kdy diskrétní regulační obvod převádíme na spojitý regulační obvod.
Na obr. 1. 2 je vidět, že při malé vzorkovací periodě může být tvarovaná akční veličina 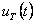 nahrazena spojitou akční veličinou
nahrazena spojitou akční veličinou 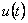 , která bude zpožděná o polovinu vzorkovací periody, tzn.
, která bude zpožděná o polovinu vzorkovací periody, tzn. 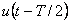 . Toto nahrazení je tedy tím lepší, čím je menší vzorkovací perioda T.
. Toto nahrazení je tedy tím lepší, čím je menší vzorkovací perioda T.
Díky tomuto faktu je možno původní regulační obvod s číslicovým regulátorem na obr. 8. 1 nahradit náhradním blokovým schématem, kdy přenos regulátoru 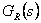 bude obsahovat dopravní zpoždění o velikosti
bude obsahovat dopravní zpoždění o velikosti 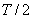 , resp.
, resp.
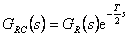 |
(8.3) |
Prakticky se však toto dopravní zpoždění přiřazuje regulované soustavě, viz obr. 8. 2.
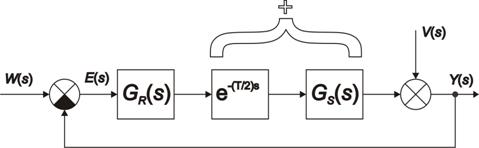
Jestliže se při analýze nebo syntéze tohoto náhradního regulačního obvodu použije metoda nevhodná pro práci s dopravním zpožděním je možno provést aproximaci (nahrazení přibližnou hodnotou) tohoto dopravního zpoždění dle vztahů
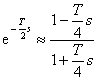 |
(8.4) |
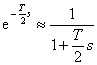 |
(8.5) |
Při použití této aproximace je nutné mít na paměti, že se jedná o přibližný přístup.
Příklad 8.1
Navrhněte regulátor pro soustavu danou přenosem 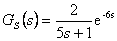 . Regulátor navrhněte nejprve pro vzorkovací periodu T = 0 s a poté pro použití s malou vzorkovací periodou T = 0,5 s. Syntézu proveďte pomocí metody požadovaného modelu (viz kapitola 8.2). Relativní překmit požadujeme okolo 5 %.
. Regulátor navrhněte nejprve pro vzorkovací periodu T = 0 s a poté pro použití s malou vzorkovací periodou T = 0,5 s. Syntézu proveďte pomocí metody požadovaného modelu (viz kapitola 8.2). Relativní překmit požadujeme okolo 5 %.
Řešení:
- T = 0 s
- Nyní navrhneme stavitelné parametry regulátoru pomocí metody požadovaného modelu (tab. 8. 3). Použijeme regulátor typu PI.
- Pro překmit 5 % zjistíme parametr
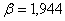 z tab. 8. 4.
z tab. 8. 4. - T = 0,5 s
- Nyní navrhneme stavitelné parametry analogového regulátoru PI pomocí metody požadovaného modelu. Návrh však bude proveden pro malou vzorkovací periodu, tzn. dopravní zpoždění soustavy, zvýšíme o
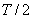 . Soustava tedy bude mít tvar
. Soustava tedy bude mít tvar - Vypočteme integrační časovou konstantu při uvažování, že vzorkovací perioda se opět považuje za T = 0 s, neboť provádíme návrh jako pro spojitý PI regulátor.
- Pro překmit 5 % zjistíme parametr
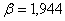 .
.
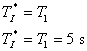
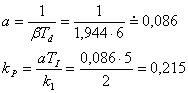
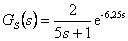
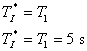
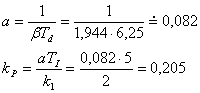
Závěr:
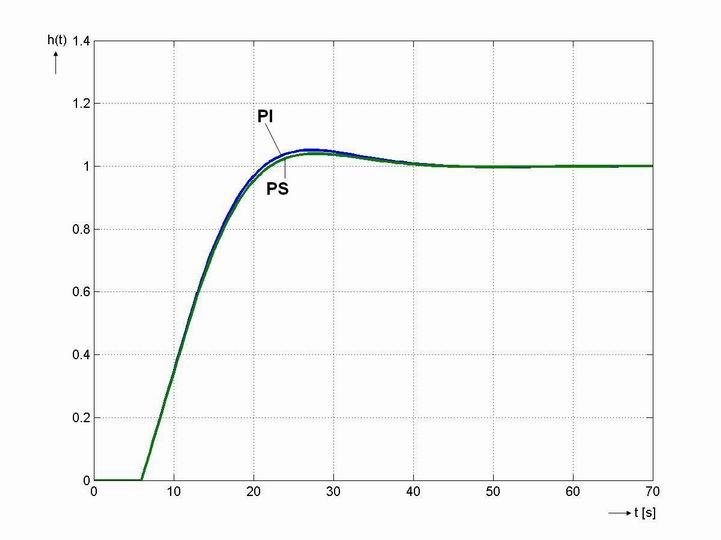
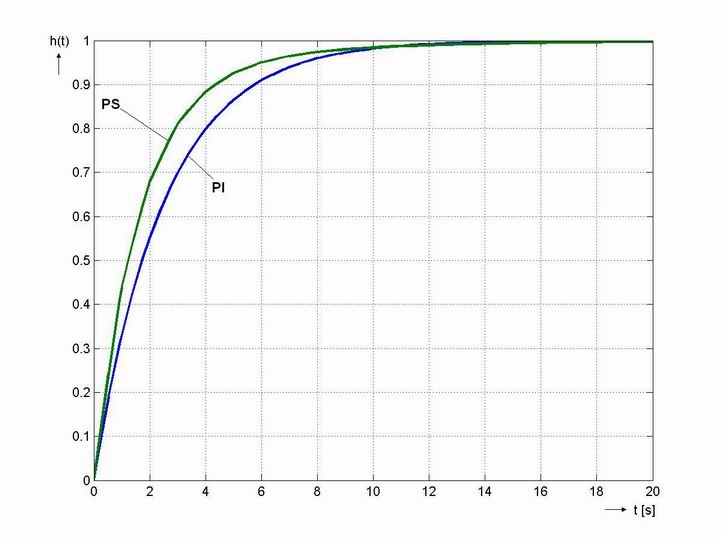
Jak je vidět dle obr. 8. 3, že průběh regulace odpovídá požadavkům. Při použití regulátoru PI byl při simulaci určen relativní překmit 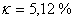 . Při seřizování regulačního obvodu pro použití PS regulátoru jsme stavitelné parametry nastavovali jako pro spojitý PI regulátor, ale soustava měla dopravní zpoždění větší o
. Při seřizování regulačního obvodu pro použití PS regulátoru jsme stavitelné parametry nastavovali jako pro spojitý PI regulátor, ale soustava měla dopravní zpoždění větší o 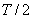 . V regulačním obvodu je poté pro vypočtené hodnoty použit regulátor typu PS. Pokud použijeme regulátor PS je relativní překmit
. V regulačním obvodu je poté pro vypočtené hodnoty použit regulátor typu PS. Pokud použijeme regulátor PS je relativní překmit 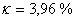 . Simulační model je k dispozici v sekci Download.
. Simulační model je k dispozici v sekci Download.
b) Pro střední vzorkovací periody T
Tento přístup je možno uvažovat při střední vzorkovací periodě, převodníky jsou součástí diskrétní regulované soustavy a obvod je tedy považován za diskrétní.
Střední vzorkovací periodu T můžeme definovat dle vztahů [Balátě, 2003]:
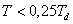 |
(8.6) |
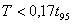 |
(8.7) |
V tomto případě využíváme při syntéze Z-transformaci.
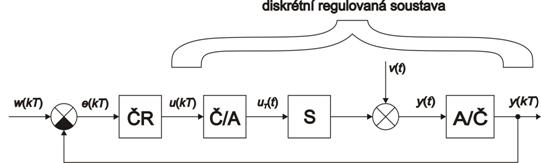
Pokud chceme provádět analýzu a syntézu takového regulačního obvodu provedeme diskretizaci přenosu soustavy. V našem případě mluvíme o tzv. přesné diskretizaci, kdy je spojitý přenos soustavy 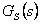 převeden na přenos v diskrétním tvaru
převeden na přenos v diskrétním tvaru 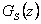 dle vztahu (při použití vzorkovače a tvarovače 0-tého řádu)
dle vztahu (při použití vzorkovače a tvarovače 0-tého řádu)
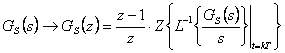 |
(8.8) |
V případě střední vzorkovací periody se využívají tzv. transformační vztahy.
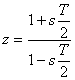 , resp. , resp. 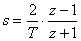 |
(8.9) |
Diskrétní přenos 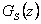 regulované soustavy transformujeme použitím transformačního vztahu (8. 9) z oblasti komplexní proměnné z do oblasti komplexní proměnné s a získáme náhradní přenos regulované soustavy
regulované soustavy transformujeme použitím transformačního vztahu (8. 9) z oblasti komplexní proměnné z do oblasti komplexní proměnné s a získáme náhradní přenos regulované soustavy 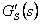 .
.
 |
(8.10) |
Zvolíme typ spojitého regulátoru 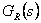 a dle metod syntézy pro spojité regulační obvody určíme hodnoty jeho stavitelných parametrů. Získaný přenos regulátoru
a dle metod syntézy pro spojité regulační obvody určíme hodnoty jeho stavitelných parametrů. Získaný přenos regulátoru 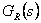 převedeme dle transformačního vztahu (8. 9) z oblasti komplexní proměnné s do oblasti komplexní proměnné z.
převedeme dle transformačního vztahu (8. 9) z oblasti komplexní proměnné s do oblasti komplexní proměnné z.
 |
(8.11) |
Příklad 8.2
Pro regulovanou soustavu s přenosem 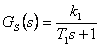 navrhněte číslicový PI regulátor. Použijte postup pro seřízení diskrétních regulačních obvodů se střední vzorkovací periodou T.
navrhněte číslicový PI regulátor. Použijte postup pro seřízení diskrétních regulačních obvodů se střední vzorkovací periodou T.
Řešení:
- Nejprve provedeme diskretizaci přenosu zadané soustavy.
- Diskretizovanou soustavu dle pravidel zpětně transformujeme do oblasti komplexní proměnné s na přenos
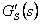 . Použijeme transformaci ve tvaru
. Použijeme transformaci ve tvaru - Po úpravě tedy dostaneme transformovaný přenos regulované soustavy ve tvaru
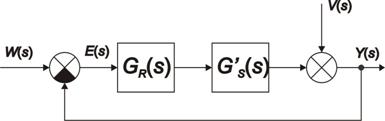
- Pro návrh a seřízení regulátoru použijeme schéma regulačního obvodu na obr. 8. 5.
- Transformovaný přenos regulované soustavy
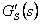 uvažuje již v sobě číslicově analogový převodník (tj. vzorkovač a tvarovač nultého řádu).
uvažuje již v sobě číslicově analogový převodník (tj. vzorkovač a tvarovač nultého řádu). - V souladu s obr. 8. 5 je přenos otevřeného regulačního obvodu dán vztahem [přenos PI regulátoru je
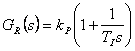 ]
] - Pro výpočet parametrů regulátoru PI použijeme metodu optimálního modulu. Nejdříve provedeme kompenzaci časových konstant, tj.
- Přenos otevřeného regulačního obvodu potom bude
- Přenos řízení po úpravě je
- kde
- Protože
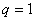 u metody optimálního modulu vycházíme z rovnic
u metody optimálního modulu vycházíme z rovnic - Po úpravě je hodnota zesílení regulátoru
- Dopočtené parametry
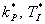 dosadíme přímo do přenosu číslicového PI regulátoru daného vztahem
dosadíme přímo do přenosu číslicového PI regulátoru daného vztahem

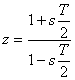

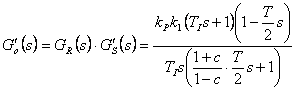
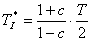
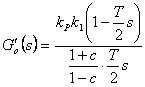
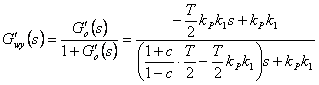
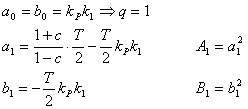
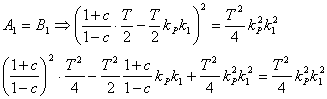
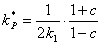
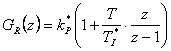
Závěr:
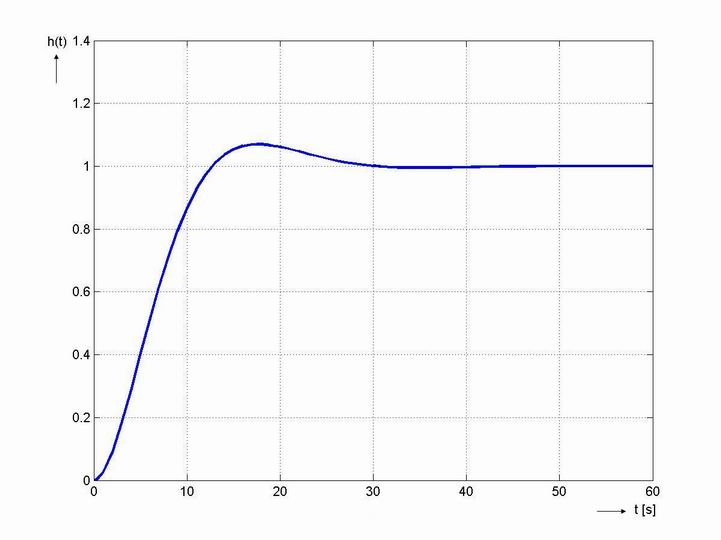
- Na obr. 8. 6 je průběh výstupní veličiny, jako odezva na jednotkový skok žádané veličiny. Byly uvažovány tyto hodnoty konstant:
- Pro srovnání je uveden průběh výstupní veličiny při použití analogového regulátoru PI s parametry
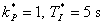 . Z průběhu vyplývá, že oba regulační obvody jsou stabilní.
. Z průběhu vyplývá, že oba regulační obvody jsou stabilní.

c) Pro velké vzorkovací periody T
Za velkou vzorkovací periodu T považujeme takovou periodu T, která nevyhovuje podmínkám (8. 1), (8. 2), (8. 6) a (8. 7).
V tomto případě, na rozdíl od předchozích přibližných metod analýzy a syntézy diskrétních regulačních obvodů získáme přesné výsledky v okamžicích vzorkování [Balátě, 2003]. Návrhy u diskrétního regulačního obvodu se provádí pouze v oblasti komplexní proměnné z, tzn. provedeme diskretizaci soustavy a pracujeme v oblasti komplexní proměnné z. Dále je nutno podotknout, že při zvyšování vzorkovací periody dochází ve větší míře k destabilizaci diskrétního regulačního obvodu.
V kapitole 8.4 jsou uvedeny metody (návrh číslicových regulátorů přímou syntézou na konečný počet kroků a Dahlinův regulátor), které jsou vhodné pro libovolnou vzorkovací periodu T, ale z výše uvedených důvodů je lepší dodržet vztahy (8. 6) a (8. 7) pro její volbu. Regulátory navržené pomocí těchto metod nejsou standardního typu.
8.2 Metoda požadovaného modelu
Metodou požadovaného modelu (dříve metoda inverze dynamiky) je možné provádět syntézu lineárních regulačních obvodů i s dominantním dopravním zpožděním [Vítečková, 2000]. Seřízení regulátoru touto metodou zaručuje nulovou trvalou regulační odchylku způsobenou skokovou změnou polohy žádané hodnoty 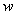 (tudíž také poruchy
(tudíž také poruchy 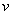 působící na výstupu regulované soustavy), což odpovídá blokovému schématu regulačního obvodu podle obr. 8. 8 [Vítečková, 1998].
působící na výstupu regulované soustavy), což odpovídá blokovému schématu regulačního obvodu podle obr. 8. 8 [Vítečková, 1998].

V případě této metody předpokládáme použití konvenčních regulátorů jak pro spojitou, tak i pro diskrétní regulaci, viz kapitola 3.1, tab. 8. 1.

Metoda požadovaného modelu umožňuje seřídit regulátor pro danou soustavu, tak aby byl zaručen požadovaný relativní překmit 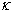 v rozsahu 0 až 50 %.
v rozsahu 0 až 50 %.
Aby bylo možné metodu požadovaného modelu použít pro seřízení regulátoru, musí být přenos regulované soustavy 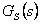 v jednom ze základních tvarů tab. 8. 3, jinak je nutno přenos upravit dle tab. 8. 2, nebo jiným způsobem [Vítečková, Víteček, 2006].
v jednom ze základních tvarů tab. 8. 3, jinak je nutno přenos upravit dle tab. 8. 2, nebo jiným způsobem [Vítečková, Víteček, 2006].
Zde si uvedeme některé postupy, jak získat přenosy regulovaných soustav ve tvaru vhodném pro metodu požadovaného modelu
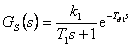 |
(8.12) |
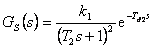 |
(8.13) |
Dopravní zpoždění 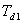 , resp.
, resp. 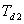 regulované soustavy je buďto přirozené nebo může vzniknout aproximací setrvačnosti vyššího řádu. Koeficient
regulované soustavy je buďto přirozené nebo může vzniknout aproximací setrvačnosti vyššího řádu. Koeficient 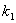 je dán ustáleným stavem přechodové charakteristiky, tedy
je dán ustáleným stavem přechodové charakteristiky, tedy
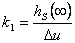 |
(8.14) |
kde 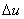 je velikost skoku akční veličiny.
je velikost skoku akční veličiny.
Další parametry 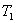 ,
, 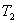 ,
, 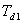 ,
, 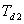 lze určit z přechodové charakteristiky soustavy (obr. 8. 9).
lze určit z přechodové charakteristiky soustavy (obr. 8. 9).
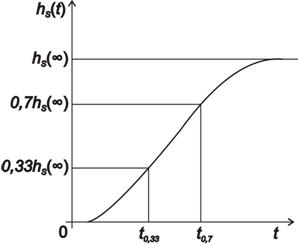
Parametry určíme dle vztahů
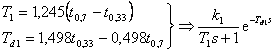 |
(8.15) |
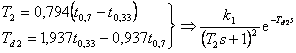 |
(8.16) |
Při identifikaci aperiodických soustav např. Strejcovou metodou [Noskievič, 1992; Švarc, Šeda, Vítečková, 2007] získáme přenos soustavy ve tvaru
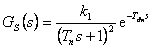 |
(8.17) |
Přenosy soustav vyššího řádu lze převést dle tab. 8. 2 v souladu se schématem
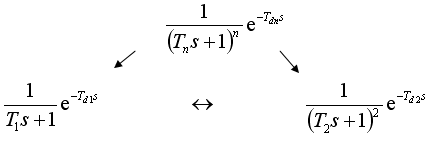 |
(8.18) |
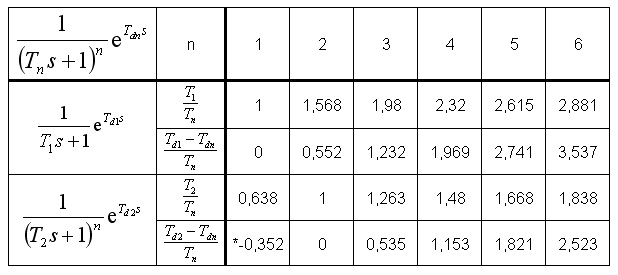
* 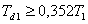
Metoda požadovaného modelu předpokládá, že požadovaný přenos řízení má tvar pro 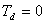 (diskrétní, spojité)
(diskrétní, spojité)
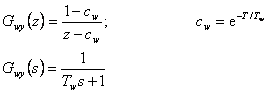 |
(8.19) |
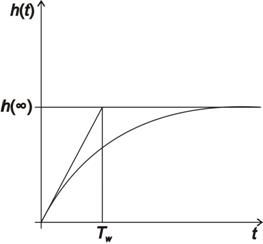
Pro regulovanou soustavu bez dopravního zpoždění 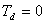 je předpokládaný průběh přechodové charakteristiky
je předpokládaný průběh přechodové charakteristiky  uzavřeného regulačního obvodu na obr. 8. 10, tedy bez relativního překmitu
uzavřeného regulačního obvodu na obr. 8. 10, tedy bez relativního překmitu 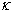 . V případě, že tedy soustava nemá dopravní zpoždění
. V případě, že tedy soustava nemá dopravní zpoždění 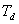 , pak musíme navrhnout časovou konstantu
, pak musíme navrhnout časovou konstantu 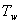 uzavřeného regulačního obvodu. Vzorkovací periodu poté volíme dle vztahu
uzavřeného regulačního obvodu. Vzorkovací periodu poté volíme dle vztahu
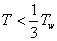 |
(8.20) |
Metoda požadovaného modelu předpokládá, že požadovaný přenos řízení má tvar pro 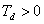 (diskrétní, spojité)
(diskrétní, spojité)
 |
(8.21) |
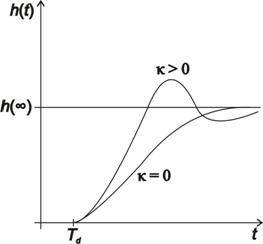
Pro regulovanou soustavu s dopravním zpožděním 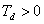 je předpokládaný průběh přechodové charakteristiky
je předpokládaný průběh přechodové charakteristiky  uzavřeného regulačního obvodu na obr. 8. 11, tedy se zvoleným relativním překmitem
uzavřeného regulačního obvodu na obr. 8. 11, tedy se zvoleným relativním překmitem 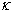 v rozsahu 0 až 50 %.
v rozsahu 0 až 50 %.
Při práci s číslicovými regulátory je nutno určit vzorkovací periodu a to v souladu s jedním z pravidel (8. 22) a (8. 23).
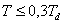 |
(8.22) |
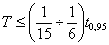 |
(8.23) |
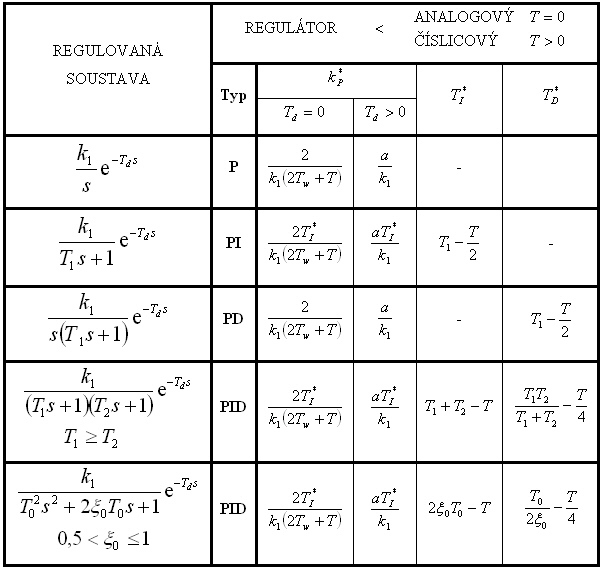
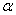 a
a 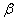 pro relativní překmit
pro relativní překmit 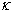 pro MPM
pro MPM
Pro parametr a platí vztah
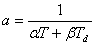 |
(8.24) |
kde 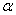 a
a 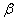 jsou dány tab. 8. 4.
jsou dány tab. 8. 4.
Příklad 8.3
Pro soustavu 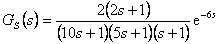 navrhněte číslicový regulátor pomocí metody požadovaného modelu, tak aby byl zajištěn překmit
navrhněte číslicový regulátor pomocí metody požadovaného modelu, tak aby byl zajištěn překmit 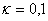 (10 %).
(10 %).
Řešení:
- Označme
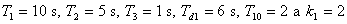
- Zadaný přenos obsahuje ve jmenovateli jeden nedominantní člen
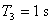 . Tento přenos můžeme upravit, tak že tento nedominantní člen převedeme do dopravního zpoždění
. Tento přenos můžeme upravit, tak že tento nedominantní člen převedeme do dopravního zpoždění 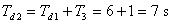 a získáme tvar
a získáme tvar - a člen získaný v čitateli přenosu opět přesuneme do dopravního zpoždění
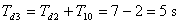 a získáme [Vítečková, Víteček, 2006]
a získáme [Vítečková, Víteček, 2006]
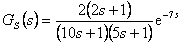
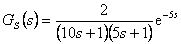
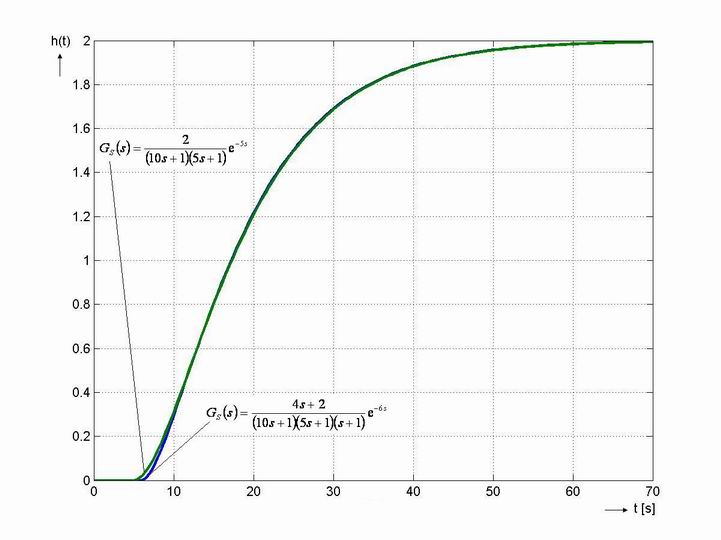
- Dle obr. 8. 12 je vidět, že aproximace původní soustavy proběhla zcela v pořádku, neboť obě přechodové charakteristiky soustav jsou téměř totožné.
- Z aproximovaného přenosu soustavy vyplývá:
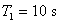 ,
, 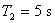 a
a 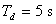 .
. - Dle tab. 8. 3 vidíme, že pro soustavu s tímto přenosem je vhodné použít PSD regulátor. Nyní můžeme určit vzorkovací periodu T podle vztahu
- Pro následující kroky zvolíme
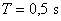 .
. - Vypočteme integrační časovou konstantu regulátoru
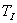 .
. - Vypočteme derivační časovou konstantu regulátoru
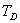 .
. - Vypočteme zesílení regulátoru
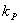 . Pro tento výpočet musíme určit hodnotu
. Pro tento výpočet musíme určit hodnotu 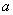 dle tab. 8. 4.
dle tab. 8. 4. - Koeficient
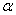 pro požadovaný překmit je
pro požadovaný překmit je 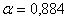 , koeficient
, koeficient 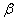 pro požadovaný překmit je
pro požadovaný překmit je 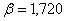 .
. - Nyní tedy můžeme vypočítat koeficient
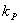 .
.
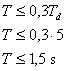
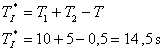
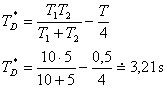
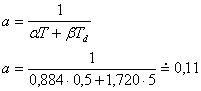
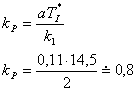
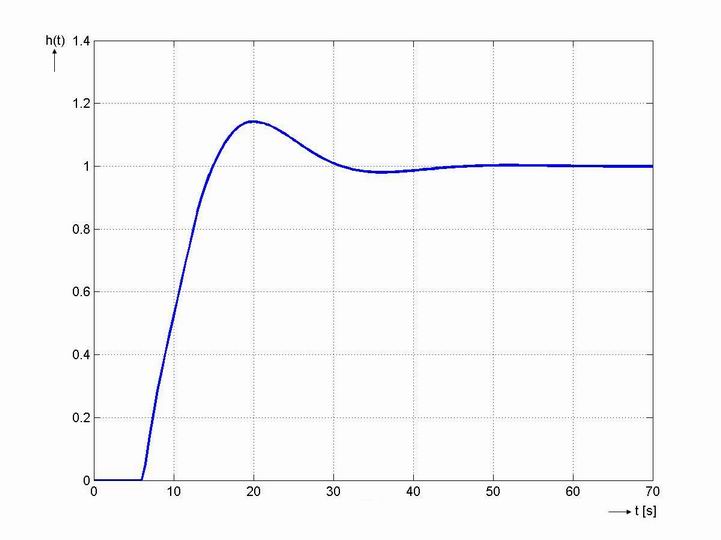
Závěr:
Jak je vidět dle obr. 8. 13 získali jsme regulační pochod, u kterého je relativní překmit vyšší než byl požadavek 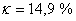 . Simulační model je k dispozici v sekci Download.
. Simulační model je k dispozici v sekci Download.
Příklad 8.4
Pro regulovanou soustavu s dopravním zpožděním 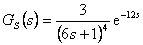 navrhněte číslicový regulátor PS a PSD pomocí metody požadovaného modelu, tak aby byl zajištěn překmit
navrhněte číslicový regulátor PS a PSD pomocí metody požadovaného modelu, tak aby byl zajištěn překmit 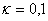 (10 %) pro vzorkovací periodu
(10 %) pro vzorkovací periodu 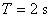 .
.
Řešení:
Vzhledem k tomu, že se jedná o soustavu vyššího řádu, musíme určit náhradní přenosy ve tvaru (8. 12) a (8. 13) za použití tab. 8. 2.
Ze zadaného přenosu regulované soustavy můžeme určit: 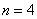 ,
, 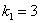 ,
, 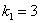 ,
, 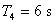 .
.
- PS
- Pro přenos ve tvaru
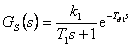 z tab. 8. 2 získáme hodnoty:
z tab. 8. 2 získáme hodnoty: - Získáváme tedy aproximaci původní soustavy ve tvaru
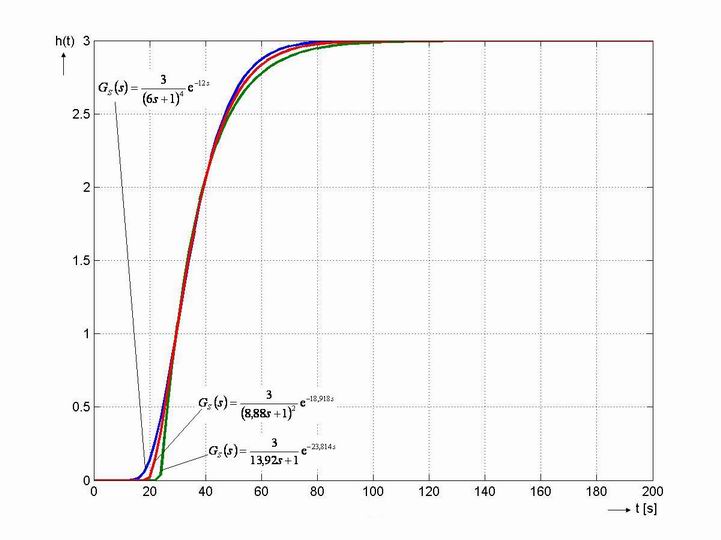
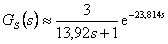 zobrazenou s původní soustavou na obr. 8. 14.
zobrazenou s původní soustavou na obr. 8. 14. - Pro nově získanou soustavu z tab. 8. 3 a tab. 8. 4 získáme:
- PSD
- Pro přenos ve tvaru
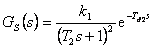 z tab. 8. 2 získáme hodnoty:
z tab. 8. 2 získáme hodnoty: - Získáváme tedy aproximaci původní soustavy ve tvaru
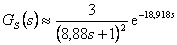 zobrazenou s původní soustavou na obr. 8. 14.
zobrazenou s původní soustavou na obr. 8. 14.
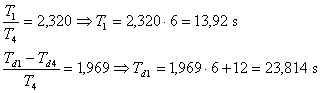
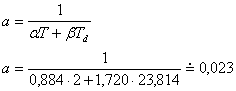
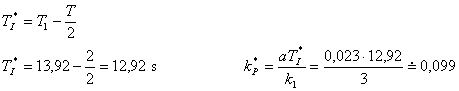
Průběh regulace je zobrazen na obr. 8. 15.
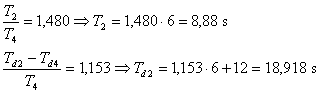
- Pro nově získanou soustavu z tab. 8. 3 a tab. 8. 4 získáme:
- Průběh regulace je zobrazen na obr. 8. 15.
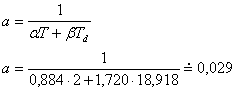
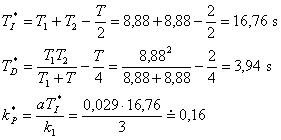
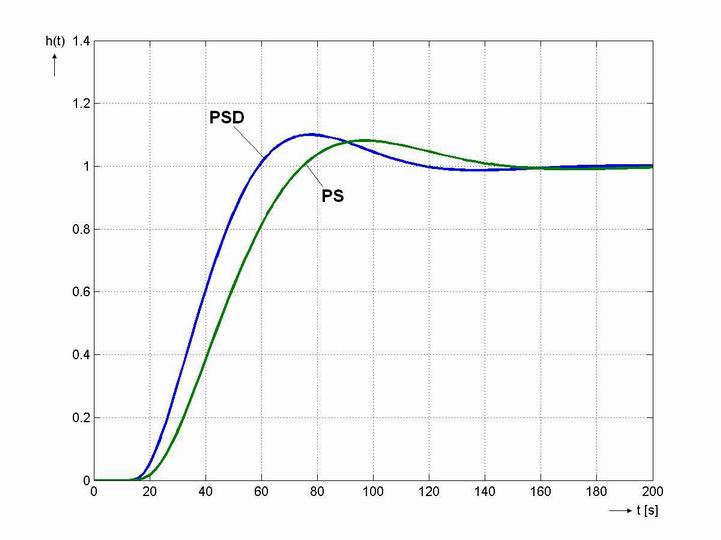
Závěr:
Jak je vidět na průběhu regulace (obr. 8. 15) metoda požadovaného modelu dává velmi kvalitní výsledky a zároveň je dodržen požadovaný překmit 10 %. V případě PS regulátoru jsme získali relativní překmit 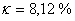 a při použití PSD regulátoru je
a při použití PSD regulátoru je 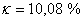 . Simulační model je k dispozici v sekci Download.
. Simulační model je k dispozici v sekci Download.
8.3 Metoda optimálního modulu
Metodou optimálního modulu je možné provádět syntézu lineárních regulačních obvodů, které neobsahují dopravní zpoždění. Metoda je užívaná jak pro spojité, tak i pro diskrétní regulační obvody. V případě diskrétních regulačních obvodů můžeme uvažovat regulační obvod dle obr. 8. 16 [Vítečková, Víteček, 2006] a dopravní zpoždění aproximovat dle vztahů (8. 4) nebo (8. 5).
Metoda optimálního modulu se používá v případě, když stupeň statismu je 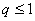 , nejčastěji však v případech kdy
, nejčastěji však v případech kdy 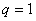 . Metoda je často používaná pro regulaci elektrických pohonů. Metoda optimálního modulu poskytuje relativní překmit regulované veličiny 5 %.
. Metoda je často používaná pro regulaci elektrických pohonů. Metoda optimálního modulu poskytuje relativní překmit regulované veličiny 5 %.

Metodou optimálního modulu stejně jako metodou požadovaného modelu seřizujeme diskrétní regulátory konvenčního typu (tab. 8. 1).
Pro vybrané regulované soustavy je sestavena tab. 8. 5.
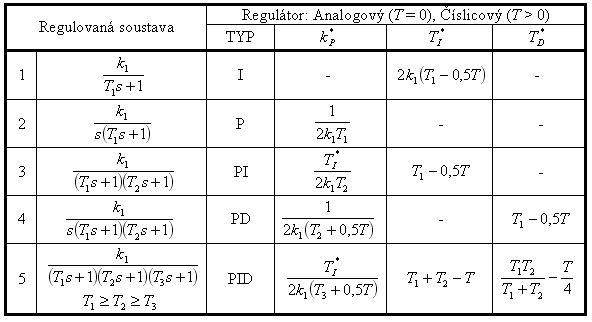
Při seřizování pomocí metody optimálního modulu se využívá tzv. kompenzace časových konstant, která je založena na vykrácení jednoho nebo dvou stabilních dvojčlenů regulované soustavy jedním dvojčlenem u regulátoru PI a PD nebo dvěma dvojčleny u regulátoru PID [Vítečková, Víteček, 2006].
Příklad 8.5
Pro regulovanou soustavu popsanou přenosem 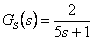 navrhněte číslicový regulátor pomocí metody optimálního modulu, který zajistí nulovou trvalou regulační odchylku pro skokovou změnu žádané
navrhněte číslicový regulátor pomocí metody optimálního modulu, který zajistí nulovou trvalou regulační odchylku pro skokovou změnu žádané 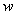 i poruchové veličiny
i poruchové veličiny 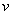 . Poruchová veličina
. Poruchová veličina 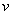 vstupuje za soustavou (obr. 8. 16).
vstupuje za soustavou (obr. 8. 16).
Řešení:
Viz tab. 8. 5 (1.řádek) je doporučeno použít diskrétní I regulátor. Vzorkovací periodu zvolíme T = 1 s.
- Nyní vypočteme integrační časovou konstantu dle vztahu
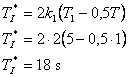
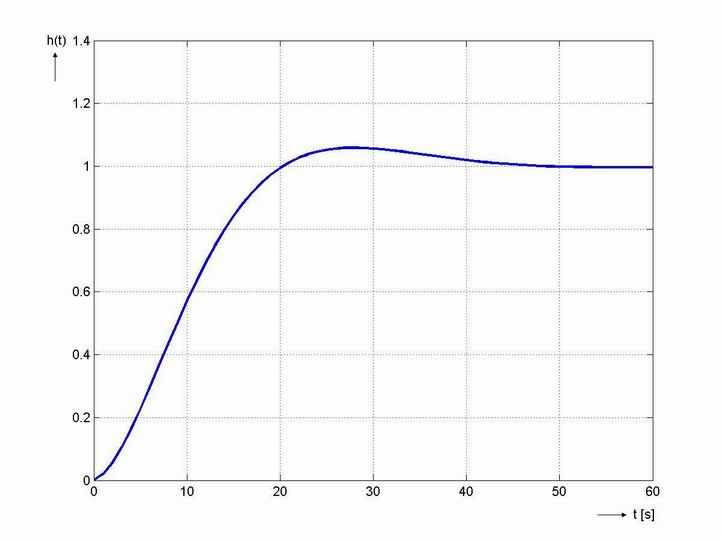
Závěr:
Jak je vidět dle průběhu přechodové charakteristiky, získali jsme regulační pochod požadované kvality, tedy s relativním překmitem okolo 5 %. Simulační model je k dispozici v sekci Download.
Příklad 8.6
Pro regulovanou soustavu popsanou přenosem 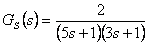 navrhněte číslicový regulátor pomocí metody optimálního modulu, který zajistí nulovou trvalou regulační odchylku pro skokovou změnu žádané w i poruchové veličiny v. Poruchová veličina vstupuje za soustavou (obr. 8. 16).
navrhněte číslicový regulátor pomocí metody optimálního modulu, který zajistí nulovou trvalou regulační odchylku pro skokovou změnu žádané w i poruchové veličiny v. Poruchová veličina vstupuje za soustavou (obr. 8. 16).
Řešení:
Viz tab. 8. 5 (3.řádek) je doporučeno použít diskrétní PI regulátor. Vzorkovací periodu zvolíme T = 1 s.
- Nyní vypočteme integrační časovou konstantu dle vztahu
- Dále vypočteme zesílení regulátoru
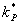
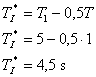
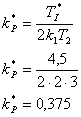
Závěr:
Jak je vidět dle průběhu přechodové charakteristiky obr. 8. 18, získali jsme regulační pochod požadované kvality, tedy s relativním překmitem okolo 5 %. Simulační model je k dispozici v sekci Download.
8.4 Návrh číslicového regulátoru přímou syntézou
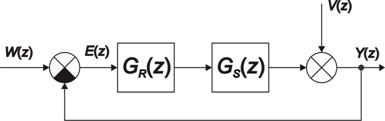
Při přímém návrhu regulátoru vycházíme ze schématu pro číslicový regulační obvod dle obr. 8. 19.
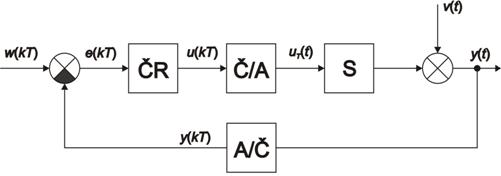
V tomto případě uvažujeme, že Č/A převodník má vlastnosti vzorkovače a tvarovače nultého řádu a dále tedy pracujeme dle obr. 8. 20 [Víteček, 2005].

Z-přenos regulované soustavy bude tedy mít tvar
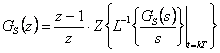 |
(8.25) |
Pro regulovanou soustavu popsanou přenosem
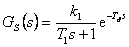 |
(8.26) |
pro
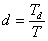 |
(8.27) |
získáme
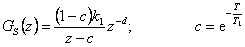 |
(8.28) |
resp.
 |
(8.29) |
Z-přenos reálné soustavy má vždy zpoždění nejméně o jednu vzorkovací periodu T viz (8. 29).
Přenos řízení diskrétního regulačního obvodu dle obr. 8. 20 je
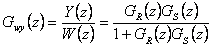 |
(8.30) |
Z tohoto přenosu jsme schopni určit přenos regulátoru 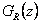 , který má tvar
, který má tvar
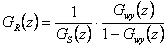 |
(8.31) |
který zajistí požadovaný přenos řízení (8. 30) pro regulovanou soustavu 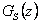 .
.
Můžeme tedy říci, že pokud požadujeme přenos řízení ve tvaru
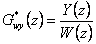 |
(8.32) |
zajistí jej regulátor daný přenosem
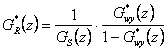 |
(8.33) |
Rovnice (8. 33) se nazývá rovnice syntézy (sythesis equation).
V závislosti na požadovaném přenosu řízení 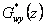 obdržíme různé regulátory. Dva z těchto regulátorů jsou:
obdržíme různé regulátory. Dva z těchto regulátorů jsou:
- regulátor na konečný počet kroků (dead-beat controller),
- Dahlinův regulátor (Dahlin controller).
8.4.1 Regulátor na konečný počet kroků
Tento typ regulátoru umožňuje při skokové změně žádané veličiny 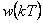 ukončit přechodový děj za dobu
ukončit přechodový děj za dobu 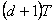 . Pro regulovanou soustavu (8. 26) to tedy znamená ukončení procesu za
. Pro regulovanou soustavu (8. 26) to tedy znamená ukončení procesu za 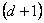 kroků.
kroků.
Tento požadavek je tedy definován přenosem řízení ve tvaru
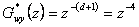 |
(8.34) |
Pokud tedy uvažujeme vztahy (8. 29) a (8. 33) získáme přenos regulátoru na konečný počet kroků daný vztahem
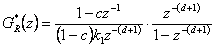 |
(8.35) |
resp.
 |
(8.36) |
Průběh přechodové charakteristiky je na obr. 8. 21.
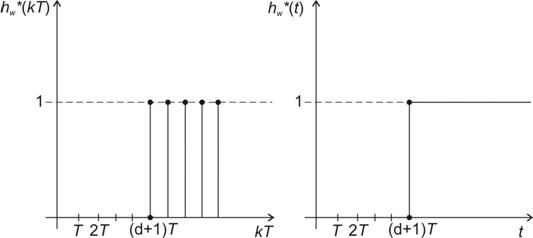
Průběh akční veličiny získáme dle
 |
(8.37) |
Průběh akční veličiny je na obr. 8. 22
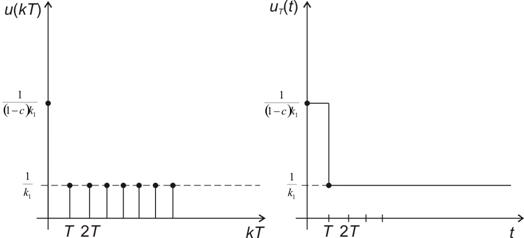
Přechodová charakteristika má zjevně ideální průběh, ale nevýhodou této metody je, že je málo robustní vůči změnám hodnoty dopravního zpoždění 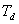 .
.
Příklad 8.7
Pro regulovanou soustavu popsanou přenosem 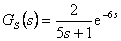 navrhněte číslicový regulátor na konečný počet kroků pro vzorkovací periodu T = 2 s.
navrhněte číslicový regulátor na konečný počet kroků pro vzorkovací periodu T = 2 s.
Řešení:
- Ze zadání můžeme určit:
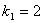 ,
, 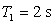 a
a 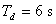
- Nejdříve je nutné provést diskretizaci zadané soustavy.
- Získáme diskretizovaný přenos ve tvaru
- resp.
- kde
- a
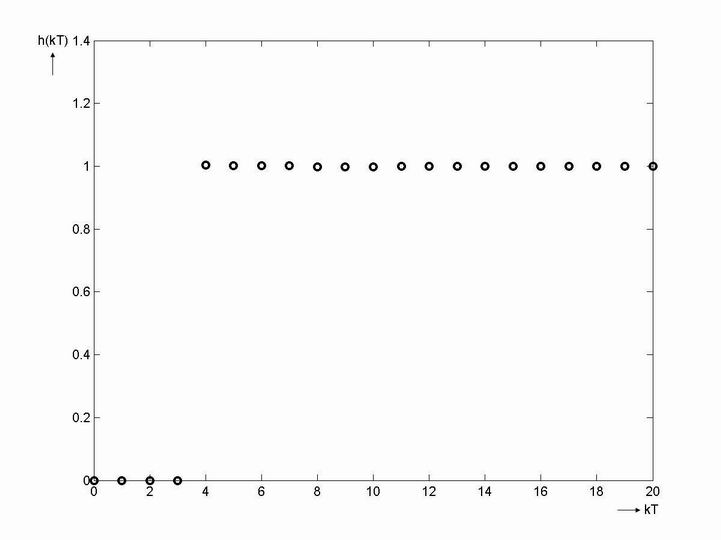
- Podle výpočtu by měla být regulace ukončena za
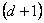 kroků, tedy po 4 krocích.
kroků, tedy po 4 krocích. - Dosadíme zadané hodnoty a získáme diskretizovaný přenos ve tvaru
- a po úpravě vhodné k simulaci v prostředí MATLAB-Simulink a získáme
- Nyní můžeme navrhnout regulátor dle
- kde dosadíme
- a získáme
- Po úpravě získáme přenos
- Přechodová charakteristika získaná simulací je zobrazena na obr. 8. 23.
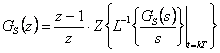
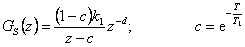

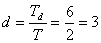
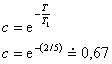

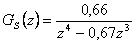
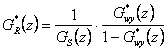
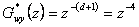
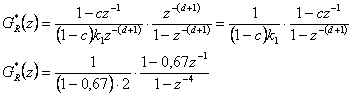
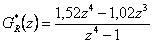
- Můžeme dále určit průběh akční veličiny
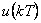 dle vztahu
dle vztahu - získáme tedy
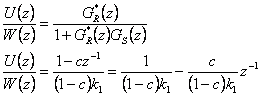
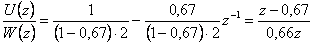
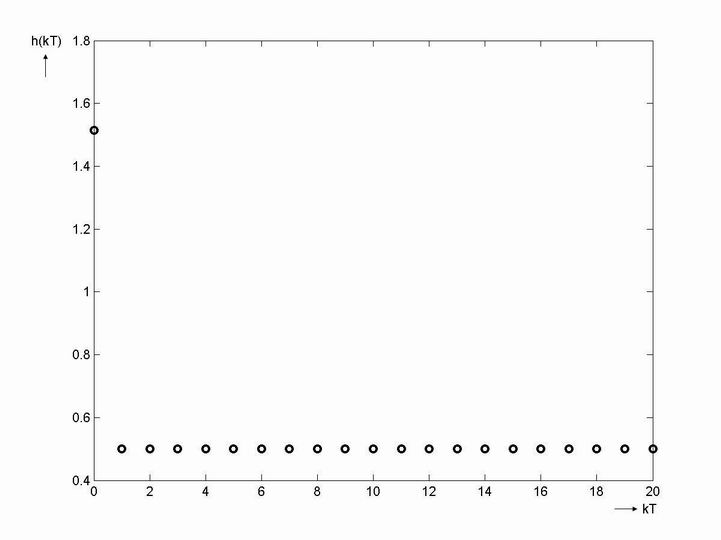
Simulační model je k dispozici v sekci Download.
8.4.2 Dahlinův regulátor
V případě Dahlinova regulátoru předpokládáme, že požadovaný Z-přenos řízení má tvar
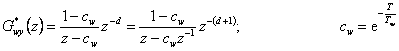 |
(8.38) |
Tento přenos řízení odpovídá požadovanému L-přenosu řízení
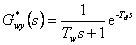 |
(8.39) |
Uvažujeme-li regulovanou soustavu popsanou přenosem
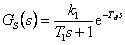 |
(8.40) |
a přenos řízení (8. 38), můžeme tedy dle rovnice syntézy (8. 33) psát s uvažováním vztahu (8. 29)
 |
(8.41) |
Průběh přechodové charakteristiky je zobrazena na obr. 8. 25.
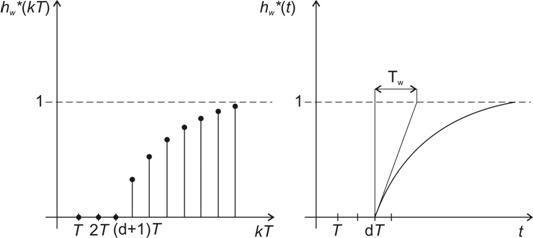
Průběh akční veličiny (obr. 8. 26) získáme dle vztahu
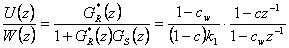 |
(8.42) |
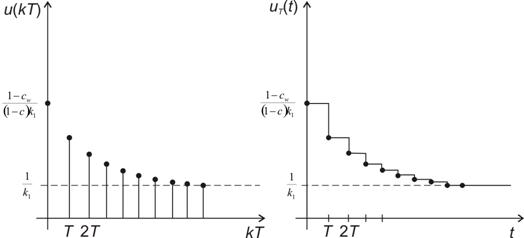
Výhodou této metody je, že oproti metodě návrhu regulátoru na konečný počet kroků je Dahlinův regulátor mnohem více robustní vůči změnám 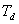 .
.
Nepříjemným jevem je tzv. zvonění (klepání) akční veličiny 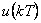 , resp.
, resp. 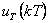 . Tento jev je způsoben záporným pólem regulátoru blízkým -1 v komplexní rovině z. Tento bod označujeme jako uzel zvonění.
. Tento jev je způsoben záporným pólem regulátoru blízkým -1 v komplexní rovině z. Tento bod označujeme jako uzel zvonění.
U Dahlinova regulátoru je toto zvonění způsobeno nevhodnou volbou časové konstanty regulačního obvodu 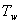 při dané vzorkovací periodě T. Rovnice syntézy pak má tvar
při dané vzorkovací periodě T. Rovnice syntézy pak má tvar
 |
(8.43) |
kde 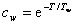
Například pro 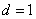 a
a 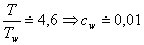 získáme
získáme
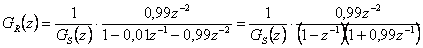 |
(8.44) |
Pól regulátoru 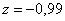 způsobuje zmíněné zvonění (obr. 8. 27a), které se však na průběhu nemusí projevit.
způsobuje zmíněné zvonění (obr. 8. 27a), které se však na průběhu nemusí projevit.
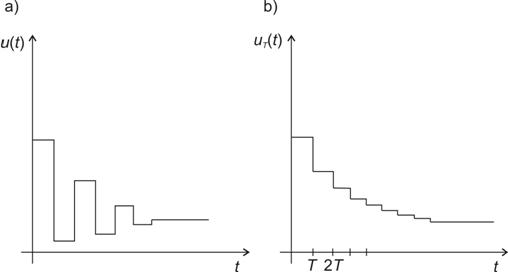
Tento tzv. zvonící pól 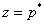 může způsobit rychlejší opotřebení akčního orgánu. Odstraněn může být dosazením do dvojčlenu
může způsobit rychlejší opotřebení akčního orgánu. Odstraněn může být dosazením do dvojčlenu 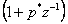 za
za 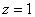 , tzn. zastoupením vztahu
, tzn. zastoupením vztahu 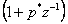 jeho ustálenou hodnotou. Např. pro (8. 44) získáme (obr. 8. 27b)
jeho ustálenou hodnotou. Např. pro (8. 44) získáme (obr. 8. 27b)
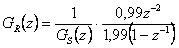 |
(8.45) |
Příklad 8.8
Pro regulovanou soustavu popsanou přenosem jako v příkladu 8.7, tedy 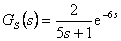 navrhněte Dahlinův číslicový regulátor pro vzorkovací periodu T = 2 s. Pomocí simulace byla zjištěna konstanta
navrhněte Dahlinův číslicový regulátor pro vzorkovací periodu T = 2 s. Pomocí simulace byla zjištěna konstanta 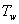 pro danou soustavu a to
pro danou soustavu a to 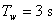 .
.
Řešení:
- Ze zadání můžeme určit:
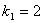 ,
, 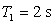 ,
, 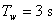 a
a 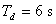
- V příkladu 8.7 jsme získali diskretizovaný přenos ve tvar
- resp.
- Dále jsme určili potřebné konstanty
- a
- Nyní vypočteme hodnotu konstanty
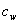 , tedy
, tedy - Podle výpočtu by měla být regulace ukončena za
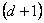 kroků, tedy po 4 krocích.
kroků, tedy po 4 krocích. - Dosadíme zadané hodnoty a získáme diskretizovaný přenos ve tvaru
- a po úpravě vhodné k simulaci v prostředí MATLAB-Simulink a získáme
- Nyní můžeme navrhnout regulátor dle
- kde dosadíme
- a získáme
- Po úpravě získáme přenos
- Přechodová charakteristika získaná simulací je zobrazena na obr. 8. 28.
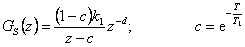

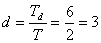
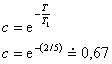


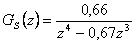
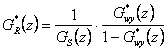
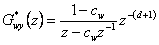

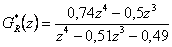
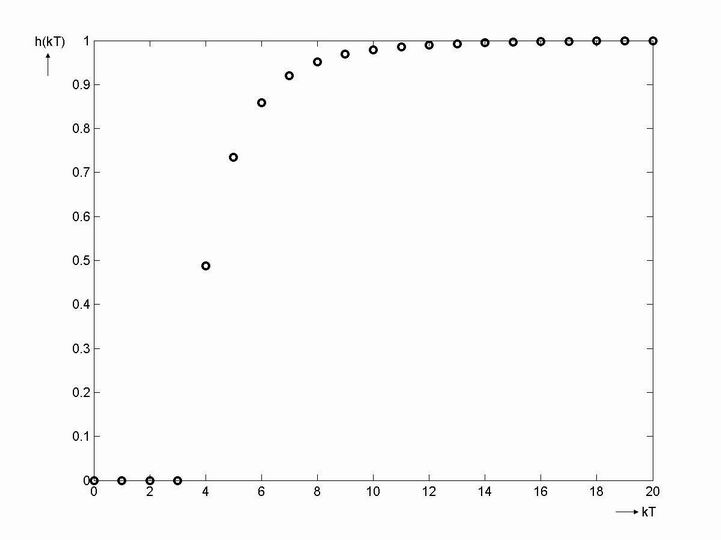
- Může dále určit průběh akční veličiny
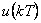 dle vztahu
dle vztahu - získáme tedy
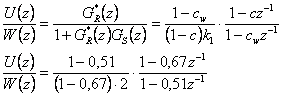
Simulační model je k dispozici v sekci Download.