1. Úvod do číslicové regulace
1.1 Význam číslicové regulace
V současném rozmachu číslicové techniky také dochází k stále častějšímu využívání číslicových regulátorů. Regulace vstupuje do našich životů v nejrůznějších formách. Ať už se jedná o přístroje, které využíváme v domácnosti či při výrobě v nejrůznějších závodech. V případě tohoto učebního textu se zaměříme na číslicové regulátory, které v diskrétní formě realizují stejné algoritmy jako analogové regulátory.
V našem případě budou pojmy jako je číslicový (diskrétní v úrovni i v čase) a diskrétní (spojitý v úrovni a diskrétní v čase) považovány za totožné neboť kvantizační chybu považujeme za zanedbatelnou [Vítečková, Víteček, 2006].
1.2 Schéma a popis číslicového regulačního obvodu
Číslicový regulační obvod je takový obvod, ve kterém alespoň jedna veličina má tvar posloupnosti diskrétních hodnot vytvářených v pravidelně se opakujících okamžicích označovaných jako perioda T.
Na obr. 1. 1 je znázorněno blokové schéma regulačního obvodu s číslicovým regulátorem.
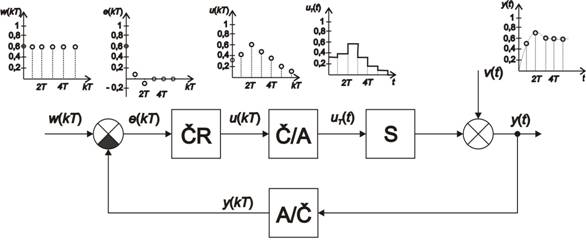
Značení bloků:
- ČR – číslicový regulátor,
- A/Č – analogově-číslicový převodník,
- S – regulovaná soustava,
- Č/A – číslicově-analogový převodník.
Značení veličin:
 – žádaná veličina,
– žádaná veličina, – regulační odchylka,
– regulační odchylka,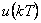 – diskrétní akční veličina,
– diskrétní akční veličina,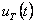 – tvarovaná akční veličina,
– tvarovaná akční veličina,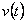 – poruchová veličina,
– poruchová veličina,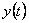 – regulovaná (výstupní) veličina,
– regulovaná (výstupní) veličina,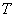 – vzorkovací perioda.
– vzorkovací perioda.
Regulovanou soustavu vždy považujeme za spojitou. O převod spojité (analogové) veličiny se stará A/Č převodník. Tento převodník je obvykle zapojen ve zpětné vazbě.
Důležitou podmínkou je, že A/Č převodník musí být přesnější než Č/A. Také se dá říci, že A/Č převodník považujeme za jakýsi omezující člen, na jehož přesnosti závisí přesnost celého regulačního obvodu.
Z číslicového regulátoru vystupuje diskrétní akční veličina u(kT), která je následně Č/A převodníkem převedena na tzv. tvarovanou veličinu 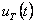 . Je zřejmé že můžeme tvarovanou veličinu jako spojitou veličinu
. Je zřejmé že můžeme tvarovanou veličinu jako spojitou veličinu 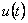 se zpožděním o velikosti
se zpožděním o velikosti 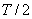 , tedy
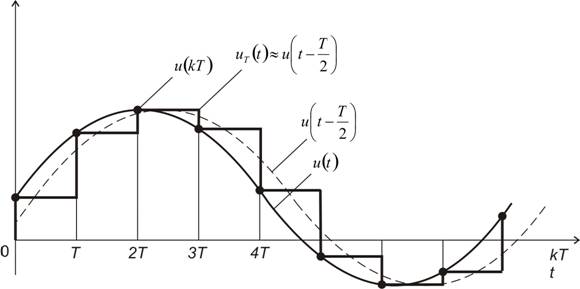
, tedy 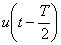 .Průběhy akčních veličin v číslicovém regulačním obvodu jsou na obr. 1. 2.
.Průběhy akčních veličin v číslicovém regulačním obvodu jsou na obr. 1. 2.
1.3 Z-transformace
Z-transformace je matematický aparát, který se využívá k popisu, analýze a syntéze diskrétních regulačních obvodů [Wittenmark, Aström, Arzen; Vítečková, 1995].
Definiční vztahy Z-transformace jsou:
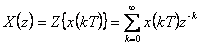 |
(1.1) |
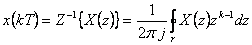 |
(1.2) |
kde
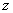 – komplexní proměnná,
– komplexní proměnná,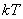 – diskrétní reálná proměnná (diskrétní čas),
– diskrétní reálná proměnná (diskrétní čas),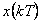 – diskrétní originál (Z-originál),
– diskrétní originál (Z-originál),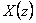 – diskrétní obraz (Z-obraz),
– diskrétní obraz (Z-obraz),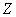 – operátor přímé Z-transformace,
– operátor přímé Z-transformace,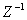 – operátor zpětné Z-transformace,
– operátor zpětné Z-transformace,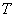 – vzorkovací perioda,
– vzorkovací perioda,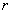 – kružnice, uvnitř které leží všechny singulární body funkce X(z)
– kružnice, uvnitř které leží všechny singulární body funkce X(z)
Zpětná Z-transformace se užívá, když hledáme k diskrétnímu obrazu X(z) originál x(kT).
Diskrétní časovou funkci x(kT) získáme ze spojité časové funkce x(t) zastoupením spojitého času t diskrétním časem x(kT), tzn.
 |
(1.3) |
Pro diskrétní časovou funkci se užívá ekvivalentní zápis
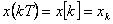 |
(1.4) |
Aby diskrétní časová funkce x(kT) byla originálem, musí být:
- a) nulová pro záporné k, tzn.
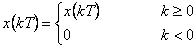 |
(1.5) |
- b) exponenciálního řádu, tzn., musí vyhovovat nerovnosti
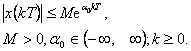 |
(1.6) |
Splnění první podmínky se dá zajistit stejně jako při L-transformaci vynásobením diskrétní časové funkce diskrétním Heavisideovým jednotkovým skokem, který je dán vztahem
 |
(1.7) |
Stejně jako u L-transformace zapisujeme korespondenci mezi diskrétním originálem a diskrétním obrazem ve tvaru
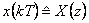 |
(1.8) |
Ukážeme si souvislost mezi L-transformací, definovanou vztahem
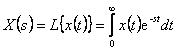 |
(1.9) |
a Z-transformací.
V definičním vztahu (1. 9) spojitý čas t zastoupíme diskrétním časem kT a spojitý integrál diskrétní sumou, dostaneme
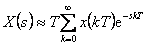 |
(1.10) |
Srovnáním vztahu (1. 10) a (1. 1) vidíme, že pro
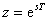 |
(1.11) |
bude platit
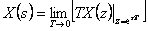 |
(1.12) |
1.3.1 Základní vlastnosti Z-transformace
Základní vlastnosti Z-transformace jsou uvedeny v tab. 1. 1. Podrobnější jsou uvedeny např. v [Vítečková, 1995; Vítečková, 2005].
| Linearita | 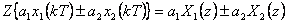 |
| Posunutí v časové oblasti vpravo (zpoždění) | 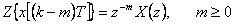 |
| Posunutí v časové oblasti vlevo (předstih) | 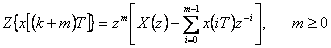 |
Dopředná diference 1. řádu 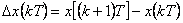 |
 |
Zpětná diference 1. řádu 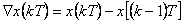 |
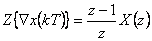 |
| Dopředná diference n-tého řádu | 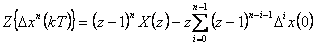 |
| Zpětná diference n-tého řádu | 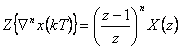 |
| Sumace v časové oblasti typu I – odpovídá dopředné diferenci [dopředná (pravá) obdélníková metoda] | 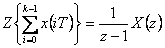 |
| Sumace v časové oblasti typu II – odpovídá zpětné diferenci [zpětná (levá) obdélníková metoda] | 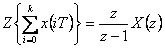 |
| Koncová hodnota v časové oblasti | 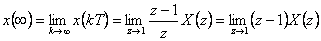 |
1.3.2 Ukázka ze slovníku L a Z-transformace
Pro ukázku je k dispozici výtah ze slovníku L a Z-transformace. Podrobněji např. v [Vítečková, 1995, Vítečková, 2005].
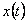 |
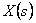 |
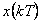 |
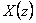 |
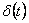 |
1 | 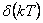 |
1 |
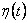 |
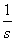 |
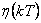 |
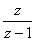 |
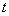 |
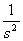 |
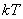 |
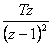 |
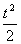 |
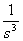 |
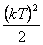 |
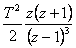 |
| - | - |  |
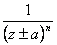 |
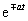 |
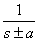 |
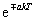 |
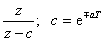 |
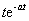 |
 |
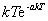 |
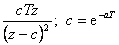 |
| - | - | 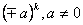 |
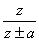 |
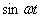 |
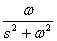 |
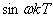 |
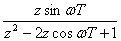 |
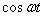 |
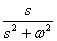 |
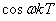 |
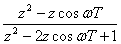 |
1.3.3 Z-transformace – řešené příklady
Příklad 1.1
Určete obraz diskrétní časové funkce na obr. 1. 3.
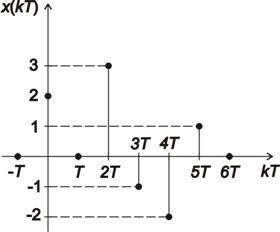
Řešení:
Z obr. 1. 3 vyplývá, že diskrétní časová funkce x(kT) je originál. V souladu s definičním vzorcem Z-transformace, obraz je dán součtem nekonečné řady, kde u mocniny 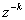 je odpovídající pořadnice diskrétní časové funkce x(kT).
je odpovídající pořadnice diskrétní časové funkce x(kT).
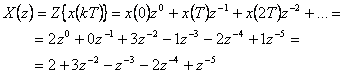
Nyní zapíšeme získaný obraz X(z) v kladných mocninách komplexní proměnné z a získáme
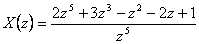
Při srovnání průběhů x(kT) a obrazu X(z) v kladných mocninách komplexní proměnné zjistíme, že diskrétní časové funkci trvající r kroků (v našem případě r = 5) odpovídá obraz, který má r-násobný nulový pól, tzn. 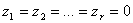 .
.
Příklad 1.2
Určete obraz diskrétní časové funkce na obr. 1. 4.
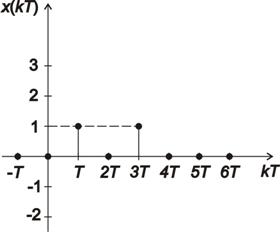
Řešení:
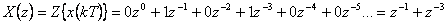
Jak je vidět z obou předchozích příkladů, nalezení obrazu, když známe časové pořadnice v jednotlivých diskrétních časových okamžicích je velmi jednoduché.
Příklad 1.3
Pomocí přímé Z-transformace určete obrazy diskrétních časových funkcí:
- 1.
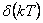
- 2.
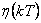
Řešení:
- 1. Diskrétní Diracův impuls je definován vztahy
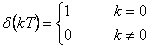
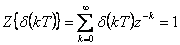
Z-obraz diskrétního Diracova impulsu je roven 1.
- 2. Dle vztahu (1. 10) píšeme
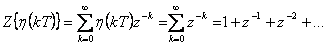
Výraz vynásobíme  .
.
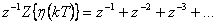
Oba předešlé vztahy odečteme a získáme
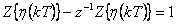
Po úpravě je Z-obraz diskrétního Heavisideova skoku:
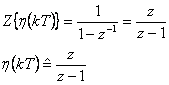
Příklad 1.4
Stanovte originál  k funkci
k funkci 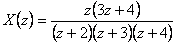 .
.
Řešení:
- Funkci
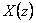 upravíme tak, že jí vydělíme z.
upravíme tak, že jí vydělíme z. - Nyní lze provést rozklad pravé strany na parciální zlomky a dosazovací metodou dopočítat koeficienty A, B a C parciálních zlomků.
- Za z dosadíme
- Po dosazení a úpravě získáme obraz funkce ve tvaru
- Pomocí slovníku L a Z-transformace z tab. 1. 2 provedeme zpětnou Z-transformaci podle vztahu
- a získáme originál k
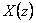
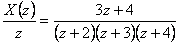
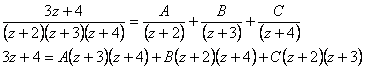
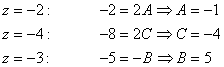
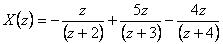
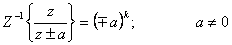
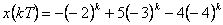
Dostali jsme řešení v tzv. uzavřeném tvaru. Hodnotu 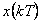 můžeme dopočítat pro libovolně velké k.
můžeme dopočítat pro libovolně velké k.
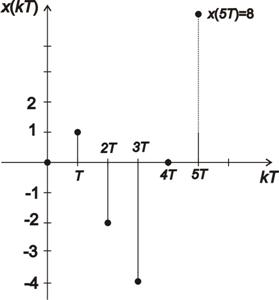
Příklad 1.5
Stanovte originál 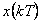 k funkci
k funkci 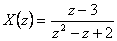 .
.
Řešení:
- Provedeme dělení mnohočlenů.
- Nyní určíme originál k funkci
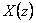
- Toto řešení je v tzv. otevřeném tvaru. Máme omezený počet hodnot originálu
 . Na obr. 1. 5 je grafické znázornění originálu funkce
. Na obr. 1. 5 je grafické znázornění originálu funkce  z příkladu 1.5.
z příkladu 1.5.
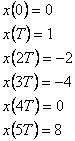
1.4 Vzorkování
Signály získané měřením v reálném prostředí jsou obecně funkce spojitého času a nabývají obvykle nekonečného počtu hodnot ze spojitého intervalu. Nazývají se analogové veličiny nebo analogové signály. Záznam těchto signálů pro jejich zpracování nebo jen prostou reprodukci v číslicových systémech (analyzátorech, číslicových počítačích) nelze uskutečnit bez jejich vzorkování a kvantování. Vzorkování je tedy operace, při které je nahrazen signál se spojitým časem posloupností vzorků [Tůma, 2006].
Pro volbu vzorkovací periody T, resp. vzorkovací frekvence 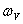 neexistují přesná pravidla, ale její volba do značné míry může ovlivnit kvalitu a stabilitu diskrétního regulačního obvodu a jeho vlastnosti [Balátě, 2003]. V tab. 1. 3 jsou vypsány doporučené hodnoty vzorkovací periody pro různá nasazení [Vítečková, Víteček, 2006].
neexistují přesná pravidla, ale její volba do značné míry může ovlivnit kvalitu a stabilitu diskrétního regulačního obvodu a jeho vlastnosti [Balátě, 2003]. V tab. 1. 3 jsou vypsány doporučené hodnoty vzorkovací periody pro různá nasazení [Vítečková, Víteček, 2006].
| Vzorkovací perioda T | Proces |
| (10 – 500) µs | přesné řízení a modelování, elektrické systémy, energetické systémy, přesné řídicí roboty |
| (0,5 – 20) µs | stabilizace výkonových systémů, letové simulátory, trenažéry |
| (10 – 100) ms | zpracování obrazů, virtuální realita, umělé vidění |
| (0,5 – 1) s | monitorování a řízení objektů, chemické procesy, elektrárny |
| (1 – 3) s | regulace průtoků |
| (1 – 5) s | regulace tlaku |
| (5 – 10) s | regulace hladiny |
| (10 – 20) s | regulace teploty |
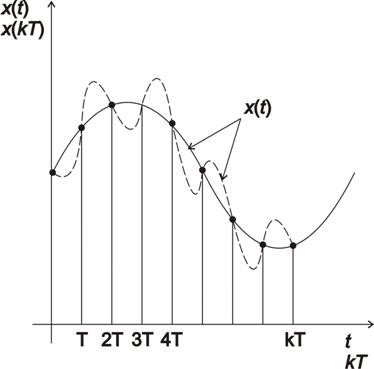
Jak je vidět na obr. 1. 6 diskrétní časové funkci x(kT) odpovídá nekonečně mnoho spojitých funkcí x(t).
Dle Shannonova–Kotelnikova teorému je pro dokonalou reprodukci spojitého signálu při převodu z číslicového tvaru nutné, aby vzorkovací frekvence 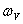 byla minimálně dvakrát větší než maximální frekvence ve spektru měřeného signálu
byla minimálně dvakrát větší než maximální frekvence ve spektru měřeného signálu 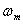 jak je uvedeno v rovnici (1. 13).
jak je uvedeno v rovnici (1. 13).
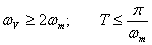 |
(1.13) |
Diskrétní časovou funkci x(kT) ze spojité časové funkce získáme x(t) nahrazením spojitého času t diskrétním časem kT.
 |
(1.14) |
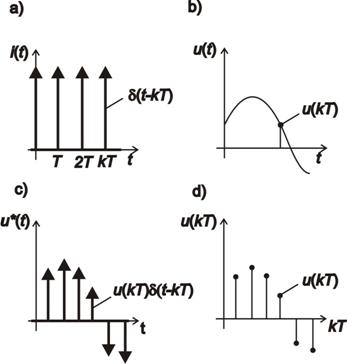
1.4.1 Vzorkovač a tvarovač
Tvarovač a vzorkovač (obr. 1. 7) převádějí spojitý signál u(t) na tvarovaný signál 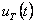 v podobě schodovité časové funkce na obr. 1. 2.
v podobě schodovité časové funkce na obr. 1. 2.

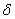 -vzorkovače a tvarovače
-vzorkovače a tvarovačeTvarovač toho typu se označuje jako tvarovač nultého řádu.
Tvarovaný signál 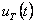 v k-tém intervalu je pomocí posunutých Heavisideových skoků dán vztahem [Víteček, 1988]
v k-tém intervalu je pomocí posunutých Heavisideových skoků dán vztahem [Víteček, 1988]
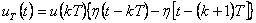 |
(1.15) |
Jak je vidět na obr. 1. 2 celý tento výraz vyjadřuje obdélník s výškou u(kT) a šířkou T. Tvarovaný signál 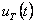 pro
pro 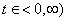 je dán vztahem
je dán vztahem
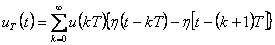 |
(1.16) |
Po provedení Laplaceovy transformace vztahu (1. 16) získáme obraz tvarovaného signálu
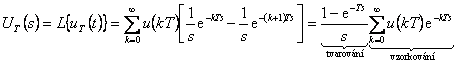 |
(1.17) |
resp.
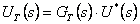 |
(1.18) |
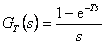 |
(1.19) |
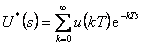 |
(1.20) |
Z předešlých vztahů je tedy viditelné, že samotný převod spojitého signálu u(t) na tvarovaný 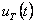 se dá rozdělit na vzorkování a následné tvarování. Vlastnosti tvarovače se dají popsat jeho přenosem (1. 19) a z tohoto přenosu se dá získat impulsní funkce.
se dá rozdělit na vzorkování a následné tvarování. Vlastnosti tvarovače se dají popsat jeho přenosem (1. 19) a z tohoto přenosu se dá získat impulsní funkce.
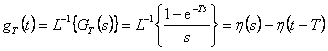 |
(1.21) |
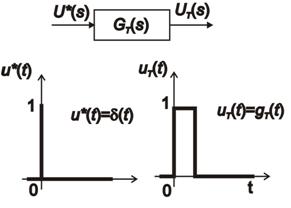
Impulsní funkce 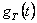 je tedy pravoúhlý impuls s jednotkovou výškou a šířkou T.
je tedy pravoúhlý impuls s jednotkovou výškou a šířkou T.
Ideálním vzorkováním spojitého signálu u(t) získáme 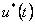 , který získáme zpětnou Laplaceovou transformací obrazu
, který získáme zpětnou Laplaceovou transformací obrazu 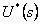 daného vztahem (1. 20).
daného vztahem (1. 20).
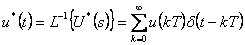 |
(1.22) |
V souladu s vlastnostmi Diracových impulsů můžeme psát
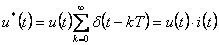 |
(1.23) |
kde
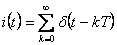 |
(1.24) |
Ze vztahu (1. 24) je vidět, že ideálně vzorkovaný signál 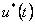 lze brát jako posloupnost Diracových impulsů i(t) modulovanou spojitým signálem u(t). Dle toho tedy můžeme říct, že vzorkovač, který převádí spojitý signál u(t) na signál vzorkovaný
lze brát jako posloupnost Diracových impulsů i(t) modulovanou spojitým signálem u(t). Dle toho tedy můžeme říct, že vzorkovač, který převádí spojitý signál u(t) na signál vzorkovaný 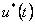 je jakousi fyzikálně realizovatelnou matematickou fikcí a proto jej nazýváme
je jakousi fyzikálně realizovatelnou matematickou fikcí a proto jej nazýváme 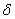 -vzorkovačem.
-vzorkovačem.
Reálný vzorkovač si většinou představujeme ve formě A/Č převodníku. Pro jednoduchost většinou 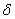 -vzorkovač od reálného vzorkovače nerozlišujeme. Mluvíme tedy pouze o vzorkovači, na jehož výstupu je vzorkovaný signál
-vzorkovač od reálného vzorkovače nerozlišujeme. Mluvíme tedy pouze o vzorkovači, na jehož výstupu je vzorkovaný signál 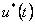 nebo diskrétní signál u(kT) [Víteček, 1988].
nebo diskrétní signál u(kT) [Víteček, 1988].