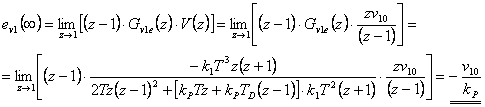7. Kvalita regulačního pochodu diskrétních regulačních obvodů
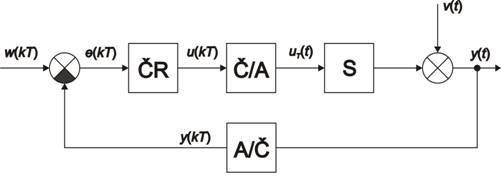
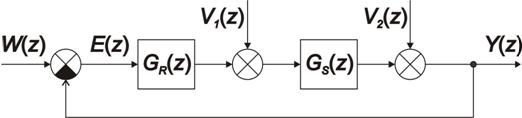
Obsahem této kapitoly je seznámení se s pojmy týkajícími se kvality regulace diskrétních regulačních obvodů (obr. 7. 1), která má přímou souvislost s návrhem regulátorů k dané regulované soustavě.
 |
(7.1) |
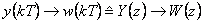 |
(7.2) |
Kvalita regulace se posuzuje ve třech oblastech:
- oblast komplexní proměnné – rozložení pólů,
- časová oblast – časové charakteristiky (přechodové, impulsní atd.),
- kmitočtová oblast – kmitočtové charakteristiky (amplitudofázové, logaritmické atd.).
Kvalita regulace se nejčastěji posuzuje v časové oblasti, tedy dle průběhu přechodové charakteristiky v závislosti na čase a také v oblasti komplexní proměnné, kdy nás zajímá rozložení pólů charakteristického mnohočlenu.
Kvalitu regulace dále vyjadřuje existence či neexistence trvalé regulační odchylky.
7.1 Časová oblast
Kvalitu regulačního pochodu v časové oblasti posuzujeme na základě průběhu regulované veličiny y(t) v závislosti na čase vyvolaného skokovou změnou (polohy) žádané veličiny  (obr. 7. 5) nebo poruchové veličiny
(obr. 7. 5) nebo poruchové veličiny 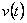 .
.
Obecně můžeme považovat vstupní skokové změny za jednotkové, tedy ve tvaru diskrétního Heavisideova jednotkového skoku 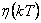 .
.
Při současném působení žádané veličiny  a poruchové veličiny
a poruchové veličiny 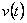 se průběhy výstupních veličin liší v označení a jsou rozlišeny pomocí indexů a platí
se průběhy výstupních veličin liší v označení a jsou rozlišeny pomocí indexů a platí
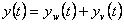 , resp. , resp. 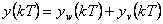 |
(7.3) |
kde 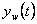 , resp.
, resp. 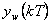 je odezva na žádanou veličinu
je odezva na žádanou veličinu  při
při 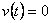 a
a 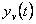 , resp.
, resp. 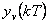 je odezva na poruchovou veličinu
je odezva na poruchovou veličinu 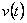 při
při 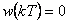 .
.
Při vykreslování časových průběhů budeme předpokládat vždy spojité průběhy, při analytických výpočtech regulačních odchylek a dalších kvalitativních parametrů budeme vycházet z obr. 7. 2, tj. budeme předpokládat diskretizovaný přenos regulované soustavy ve tvaru
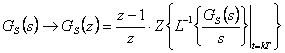 |
(7.4) |
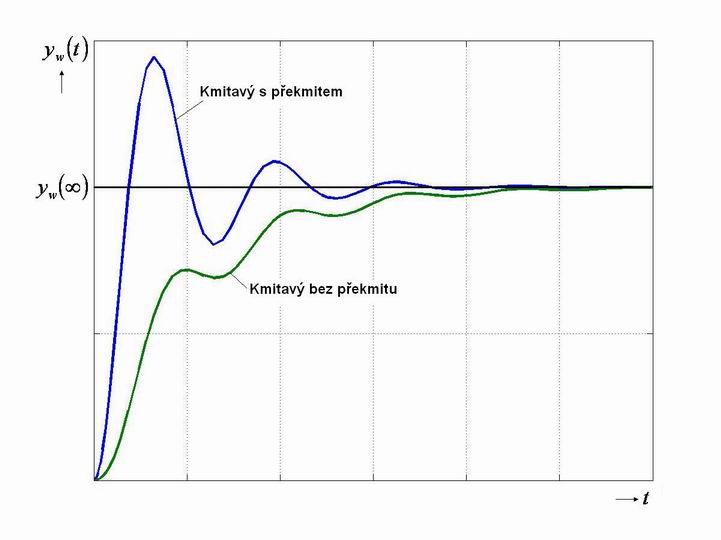
Průběh regulované veličiny můžeme rozdělit:
- Kmitavý (obr. 7. 3):
- s překmitem,
- bez překmitu.
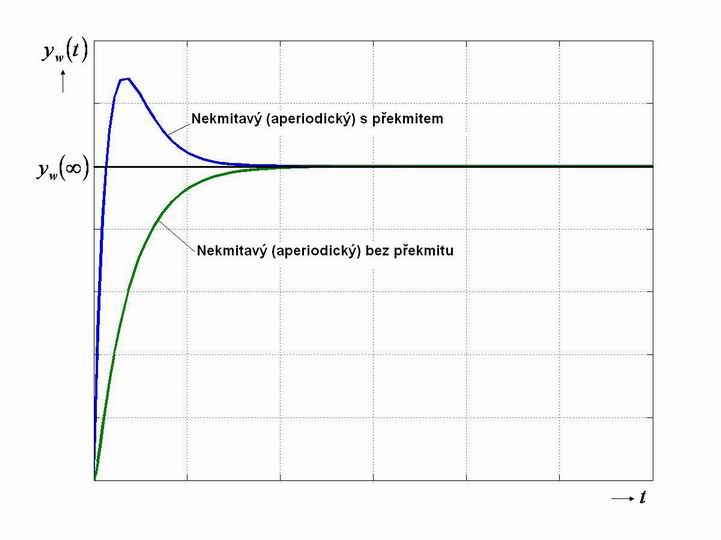
- Nekmitavý (aperiodický) (obr. 7. 4):
- s překmitem,
- bez překmitu.
Nyní se můžeme zaměřit na vyhodnocení samotného průběhu regulované veličiny obr. 7. 5 a její popis. Na tomto průběhu nás zajímají hlavně parametry, jimiž jsou relativní překmit 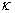 a samotná doba regulace
a samotná doba regulace 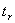 .
.
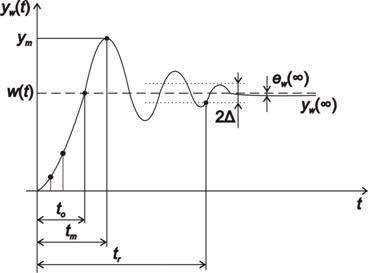
Značení veličin dle obr. 7. 5:
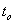 – doba odezvy (první dosažení žádané veličiny),
– doba odezvy (první dosažení žádané veličiny),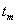 – doba dosažení maximální hodnoty regulované veličiny
– doba dosažení maximální hodnoty regulované veličiny 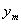 ,
,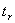 – doba regulace,
– doba regulace,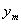 – maximální hodnota regulované veličiny,
– maximální hodnota regulované veličiny, – žádaná veličina,
– žádaná veličina,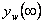 – ustálená hodnota regulované veličiny,
– ustálená hodnota regulované veličiny,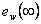 – trvalá regulační odchylka (
– trvalá regulační odchylka (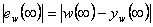 ),
),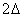 pásmo regulace (
pásmo regulace ( = 0,02 - 0,05, neměla by překročit 5 %
= 0,02 - 0,05, neměla by překročit 5 % 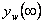 ).
).
Relativní překmit 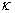 průběhu regulované veličiny určíme dle vztahu
průběhu regulované veličiny určíme dle vztahu
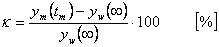 |
(7.5) |
Doba regulace 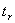 – je čas, kdy se regulovaná veličina
– je čas, kdy se regulovaná veličina 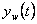 dostane do regulačního pásma
dostane do regulačního pásma 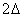 a už jej neopustí.
a už jej neopustí.
7.1.1 Sumační kritéria
Pro komplexní zhodnocení kvality regulačního pochodu jsou vhodná sumační kritéria. Sumační kritéria hodnocení kvality regulace se nejčastěji definují s lineární nebo kvadratickou závislostí na regulační odchylce. Tato kritéria jsou označovány jako kritéria lineární nebo kvadratické regulační plochy. Posouzení kvality regulačního pochodu se vyhodnocuje na základě regulační plochy (dále v obrazcích vyšrafovaná). Čím je tato regulační plocha menší, tím je kvalita regulace vyšší. Popsány budou tyto sumační kritéria.
1. Lineární regulační plocha – IE
Jedná se o základní kritérium. Pro toto kritérium je nutné, aby se jednalo o nekmitavý průběh. Jinak dojdeme k závěru, že regulační plocha je minimální, jestliže se plochy pod kladnými a zápornými půlvlnami odečtou, k čemuž dochází při kmitavém průběhu na mezi stability.
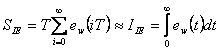 |
(7.6) |
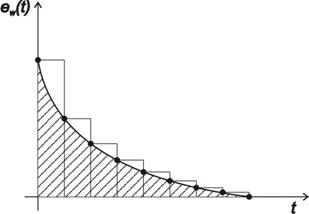
Kritérium je velmi snadno analyticky řešitelné dle vztahů
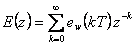 |
(7.7) |
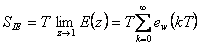 |
(7.8) |
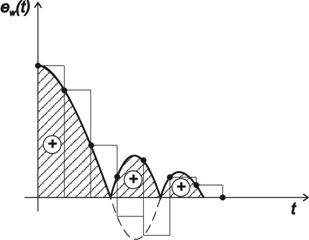
2. Absolutní regulační plocha – IAE
Nedostatky kritéria ILE odstraňuje kritérium IAE výpočtem integrálu z absolutní hodnoty regulační odchylky. Toto kritérium je tedy vhodné i pro kmitavé procesy. Hodnotu regulační plochy nejsme schopni určit analyticky. Důvodem je, že v bodech ve kterých 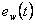 mění své znaménko, neexistuje derivace.
mění své znaménko, neexistuje derivace.
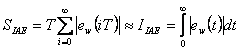 |
(7.9) |
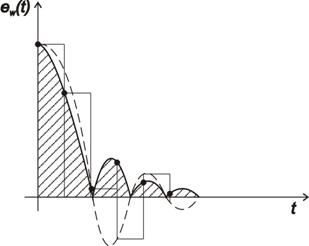
3. Kvadratická regulační plocha – ISE
Kritérium ISE je vhodné jak pro kmitavé tak i nekmitavé regulační pochody. Regulační plochu je možno určit analyticky, ale výsledný průběh regulované veličiny je kmitavý.
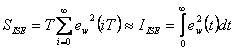 |
(7.10) |
4. ITAE
Předešlá kritéria nebrala v úvahu dobu regulace. U kritéria ITAE dochází díky zahrnutí času jak minimalizaci regulační plochy, tak minimalizaci doby regulace 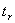 . Regulační plochu nejsme schopni určit analyticky, ale pouze simulačně.
. Regulační plochu nejsme schopni určit analyticky, ale pouze simulačně.
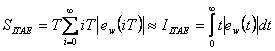 |
(7.11) |
7.1.2 Trvalé regulační odchylky
Jedním z parametrů vyjadřujících kvalitu regulace je existence či neexistence trvalých regulačních odchylek. Trvalá regulační odchylka může nabývat hodnot tab. 7. 1.
 |
Žádoucí |
 |
Zvláštní pozornost při nastavování regulátoru |
 |
Nutná změna typu regulátoru |
Odezva regulačního obvodu na skokovou změnu žádané veličiny  a poruchové veličiny
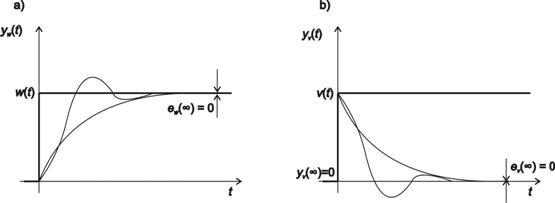
a poruchové veličiny 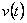 působící na výstupu regulované soustavy s nulovými trvalými regulačními odchylkami je zobrazen na obr. 7. 9. Tento průběh odpovídá stavu, kdy otevřený regulační obvod obsahuje alespoň jeden sumační člen.
působící na výstupu regulované soustavy s nulovými trvalými regulačními odchylkami je zobrazen na obr. 7. 9. Tento průběh odpovídá stavu, kdy otevřený regulační obvod obsahuje alespoň jeden sumační člen.
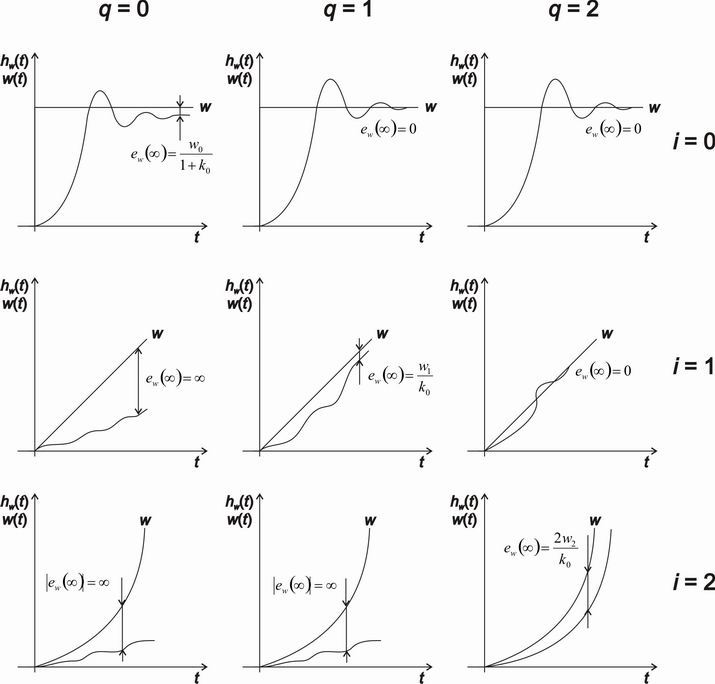
Počet sumačních členů v otevřeném regulačním obvodu označujeme jako stupeň astatismu q. Sumační člen může být obsažen jak v soustavě tak v regulátoru.
Stupeň astatismu můžeme také definovat jako nejvyšší mocninu 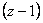 , kterou můžeme vytknout ze jmenovatele přenosu otevřeného regulačního obvodu
, kterou můžeme vytknout ze jmenovatele přenosu otevřeného regulačního obvodu 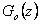 , tedy
, tedy
 |
(7.12) |
Pro
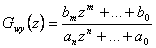 |
(7.13) |
platí
 |
(7.14) |
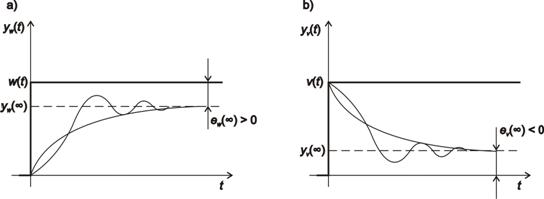
Odezva regulačního obvodu s trvalými regulačními odchylkami je na obr. 7. 10. Tento průběh odpovídá stavu, kdy otevřený regulační obvod neobsahuje ani jeden sumační člen a tedy stupeň astatismu je q = 0.
Trvalé regulační odchylky můžeme snadno určit. Vycházet budeme ze vztahu
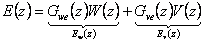 |
(7.15) |
kde 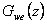 je odchylkový přenos řízení,
je odchylkový přenos řízení, 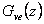 je odchylkový přenos poruchy,
je odchylkový přenos poruchy, 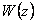 je obraz žádané veličiny a
je obraz žádané veličiny a 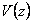 obraz poruchové veličiny.
obraz poruchové veličiny.
Nyní můžeme určit samotné regulační odchylky.
Trvalá regulační odchylka
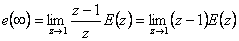 |
(7.16) |
Trvalá regulační odchylka způsobená žádanou veličinou
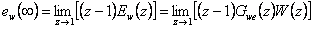 |
(7.17) |
Trvalá regulační odchylka způsobená poruchovou veličinou
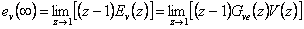 |
(7.18) |
V případě výpočtu trvalé regulační odchylky poruchové veličiny je třeba rozlišit, zda porucha vstupuje před soustavou 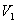 nebo porucha působí za soustavou
nebo porucha působí za soustavou 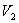 (obr. 7. 11).
(obr. 7. 11).
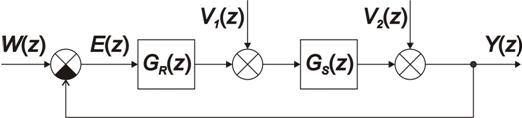
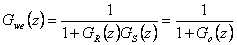 |
(7.19) |
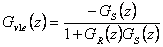 |
(7.20) |
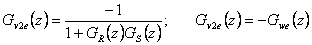 |
(7.21) |
Pro stanovení trvalých regulačních odchylek se používají tzv. testovací signály.
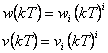 |
(7.22) |
1. Skok polohy (i = 0)
Jedná se o signál ve tvaru diskrétního Heavisideova skoku 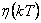 . Testovací signál je definován vztahem
. Testovací signál je definován vztahem
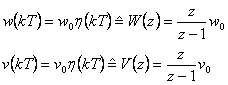 |
(7.23) |
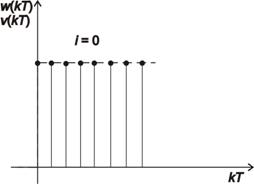
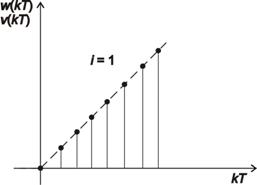
2. Skok rychlosti (i = 1)
Testovací signál je definován vztahem
 |
(7.24) |
3. Skok zrychlení (i = 2)
Testovací signál je definován vztahem
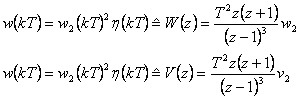 |
(7.25) |
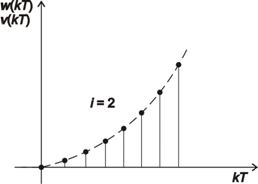
Obecně můžeme napsat obraz žádané veličiny ve tvaru
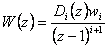 |
(7.26) |
kde
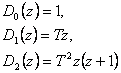
Pro přenos otevřeného regulačního obvodu platí vztah
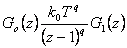 |
(7.27) |
kde
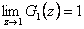
Pak pro odchylkový přenos řízení (7.19) platí
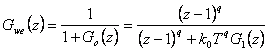 |
(7.28) |
Vztahy (7. 26) a (7. 28) dosadíme do (7. 17) a dostaneme
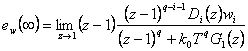 |
(7.29) |
Ze vztahu (7. 29) tedy vyplývá
 |
(7.30) |
-
kde
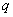 – stupeň astatismu (typ regulačního obvodu),
– stupeň astatismu (typ regulačního obvodu),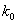 – zesílení přenosu otevřeného regulačního obvodu
– zesílení přenosu otevřeného regulačního obvodu 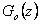 .
.
Podobné vztahy budou platit i pro regulační odchylku způsobenou poruchou na výstupu regulované soustavy  , pokud bude platit vztah (7. 21).
, pokud bude platit vztah (7. 21).
7.2 Oblast komplexní proměnné
V případě posuzování kvality regulace v oblasti komplexní proměnné z sledujeme rozmístění pólů přenosu řízení  .
.
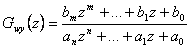 |
(7.31) |
Základním předpokladem v takovémto případě je, že regulační obvod je stabilní. Tedy v případě diskrétních regulačních obvodů bude velikost všech kořenů charakteristického mnohočlenu menší než 1, resp. stabilní oblast u diskrétních regulačních obvodů je uvnitř jednotkové kružnice v oblasti komplexní proměnné z.
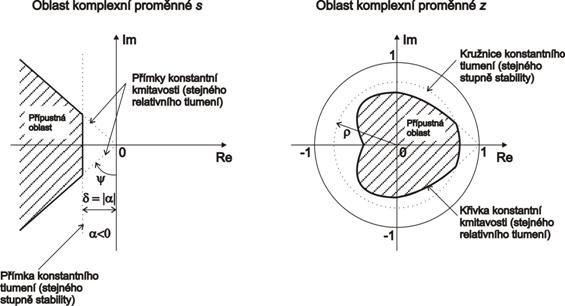
Dle obr. 7. 16 můžeme říci, že:
| Póly, které v přípustné oblasti leží nejblíže hranici přípustné oblasti, jsou dominantní. |
Požadujeme-li nekmitavý (aperiodický) průběh regulačního pochodu, musí póly být reálné z intervalu 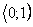 dle obr. 7. 17 (viz tab. 6. 1).
dle obr. 7. 17 (viz tab. 6. 1).
V případě roviny s výsledný relativní překmit 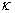 určují dvě přímky konstantní kmitavosti se stejným relativním tlumením, které svírají úhel
určují dvě přímky konstantní kmitavosti se stejným relativním tlumením, které svírají úhel 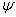 (obr. 7. 16), výraz
(obr. 7. 16), výraz 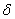 (obr. 7. 16) vyjadřuje míru stability (stupeň stability), resp. rychlost odezvy regulačního obvodu, který ovlivňuje dobu regulace danou vztahem
(obr. 7. 16) vyjadřuje míru stability (stupeň stability), resp. rychlost odezvy regulačního obvodu, který ovlivňuje dobu regulace danou vztahem
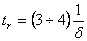 |
(7.32) |
Z obr. 7. 16 je zřejmé, že dle požadavku na kvalitu regulace je možné v rovině s a v rovině z vymezit určitou přípustnou oblast ovlivněnou dobou regulace 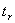 a maximálním překmitem
a maximálním překmitem 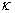 . Přípustná oblast je vymezena
. Přípustná oblast je vymezena
 |
(7.33) |
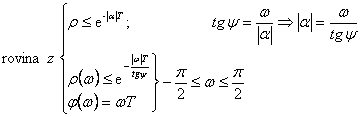 |
(7.34) |
Vztahy (7. 34) vyplývají z transformace komplexní roviny s do komplexní roviny z dané vztahem 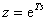 .
.
7.3 Řešené příklady
Příklad 7.1
Určete trvalou regulační odchylku žádané veličiny a poruchové veličiny (porucha 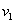 vstupuje před soustavou, porucha
vstupuje před soustavou, porucha 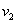 vstupuje za soustavou) pro regulační obvod s diskrétním regulátorem typu P s přenosem
vstupuje za soustavou) pro regulační obvod s diskrétním regulátorem typu P s přenosem 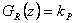 a soustavou danou přenosem
a soustavou danou přenosem 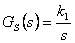 . Regulační odchylky určete pro všechny typy testovacích signálů.
. Regulační odchylky určete pro všechny typy testovacích signálů.
Řešení:
- Provedeme diskretizaci soustavy (tab. 1. 2).
- Nyní určíme odchylkový přenos řízení.


Trvalá regulační odchylka pro žádanou veličinu pro tři testovací signály:
- 1. Skok polohy
- 2.Skok rychlosti
- 3. Skok zrychlení
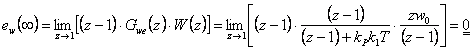


Pro 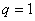 výsledky odpovídají vztahům (7. 30).
výsledky odpovídají vztahům (7. 30).
Trvalá regulační odchylka pro poruchovou veličinu:
a) Porucha 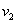 vstupuje za soustavou
vstupuje za soustavou
- Trvalé regulační odchylky
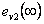 jsou podobné jako
jsou podobné jako 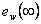 , ale s opačným znaménkem, protože
, ale s opačným znaménkem, protože 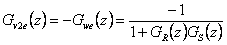 , tj.
, tj.
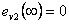 pro
pro 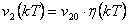
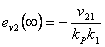 pro
pro 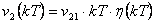
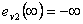 pro
pro 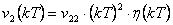
b) Porucha 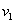 vstupuje před soustavou
vstupuje před soustavou
- Nyní určíme odchylkový přenos poruchy.
- 1. Skok polohy
- 2.Skok rychlosti
- 3. Skok zrychlení
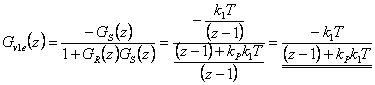
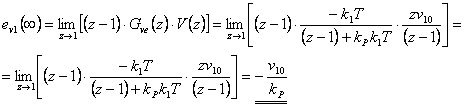


Vidíme, že 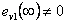 již pro skok polohy. Z toho vyplývá, že je vhodné použít místo regulátoru typu P regulátor typu PS. Simulační model je k dispozici v sekci Download.
již pro skok polohy. Z toho vyplývá, že je vhodné použít místo regulátoru typu P regulátor typu PS. Simulační model je k dispozici v sekci Download.
Příklad 7.2
Určete trvalou regulační odchylku žádané veličiny a poruchové veličiny (porucha 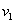 vstupuje před soustavou) pro regulační obvod s diskrétním regulátorem typu PS s přenosem
vstupuje před soustavou) pro regulační obvod s diskrétním regulátorem typu PS s přenosem 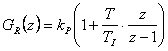 a soustavou danou přenosem
a soustavou danou přenosem 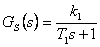 . Regulační odchylky určete pro všechny typy testovacích signálů.
. Regulační odchylky určete pro všechny typy testovacích signálů.
Řešení:
- Provedeme diskretizaci soustavy (tab. 1. 2).
- Upravíme přenos regulátoru.
- Nyní určíme odchylkový přenos řízení.

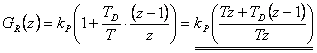

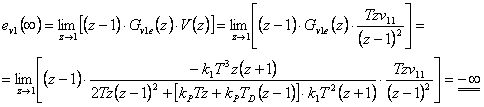
Trvalá regulační odchylka pro žádanou veličinu pro tři testovací signály:
- 1. Skok polohy
- 2.Skok rychlosti
- 3. Skok zrychlení
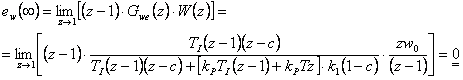
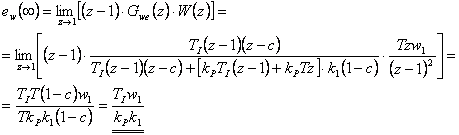

Trvalá regulační odchylka pro poruchovou veličinu (porucha 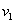 vstupuje před soustavou):
vstupuje před soustavou):
- Nyní určíme odchylkový přenos poruchy.
- 1. Skok polohy
- 2.Skok rychlosti
- 3. Skok zrychlení
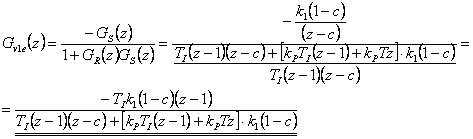
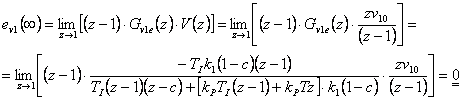

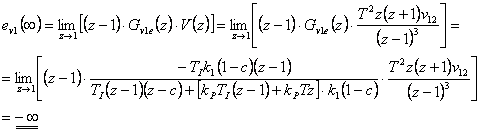
Je vidět, že u proporcionální soustavy je regulační odchylka způsobená poruchovou ve tvaru skoku polohy vstupující před soustavou nulová, na rozdíl od příkladu 7.1, kde byla integrační regulovaná soustava. Simulační model je k dispozici v sekci Download.
Příklad 7.3
Určete trvalou regulační odchylku žádané veličiny a poruchové veličiny (porucha 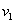 vstupuje před soustavou) pro regulační obvod s diskrétním regulátorem typu PD s přenosem
vstupuje před soustavou) pro regulační obvod s diskrétním regulátorem typu PD s přenosem 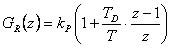 a soustavou danou přenosem
a soustavou danou přenosem 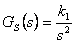 . Regulační odchylky určete pro všechny typy testovacích signálů.
. Regulační odchylky určete pro všechny typy testovacích signálů.
Řešení:
- Provedeme diskretizaci soustavy (tab. 1. 2).
- Upravíme přenos regulátoru.
- Nyní určíme odchylkový přenos řízení.

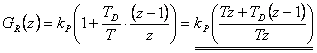

Trvalá regulační odchylka pro žádanou veličinu pro tři testovací signály:
- 1. Skok polohy
- 2.Skok rychlosti
- 3. Skok zrychlení



Trvalá regulační odchylka pro poruchovou veličinu (porucha 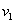 vstupuje před soustavou):
vstupuje před soustavou):
- Nyní určíme odchylkový přenos poruchy.
- 1. Skok polohy
- 2.Skok rychlosti
- 3. Skok zrychlení