6. Stabilita lineárních diskrétních regulačních obvodů
Pro diskrétní systémy platí stejná definice stability jako pro systémy spojité.
| Systém je stabilní, když se po odeznění vstupního signálu vrátí zpět do rovnovážného stavu. |
| BIBO (BOUNDED INPUT BOUNDED OUTPUT) stabilita – systém je stabilní, když na omezený vstupní signál dostaneme omezený výstupní signál. |
Stabilita je základní charakteristickou vlastností systémů, tzn. nezávisí na vstupech ani na výstupech.
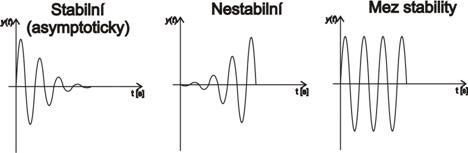
Z hlediska stability rozlišujeme regulační obvod (asymptoticky) stabilní, na mezi stability a nestabilní (obr. 6. 1). Obrázek zobrazuje stavy spojitého systému. Vždy se vyžaduje, aby regulační obvod byl za všech okolností stabilní.
6.1 Stabilita spojitých a diskrétních systémů
Mezi stabilitou spojitých a diskrétních systémů existuje spojitost. Pro názornost je vhodné připomenout nutnou a postačující podmínku stability spojitých systémů (v následující kapitole) a následně navázat s nutnou a postačující podmínkou stability systémů diskrétních.
6.1.1 Stabilita spojitých systémů
Při vyšetřování stability se vychází z tzv. charakteristického mnohočlenu, který vystupuje ve jmenovateli všech základní přenosů regulačního obvodu.
Pro spojité regulační obvody je nutná a postačující podmínka stability (NPP) formulována takto:
Regulační obvod je (asymptoticky) stabilní právě tehdy, když všechny kořeny 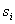 charakteristické rovnice mají záporné reálné části, tedy leží-li v levé komplexní polorovině. charakteristické rovnice mají záporné reálné části, tedy leží-li v levé komplexní polorovině. |
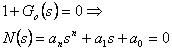 |
(6.1) |
 |
(6.2) |
Stabilní oblast komplexní roviny s je vyznačena na obr. 6. 2.
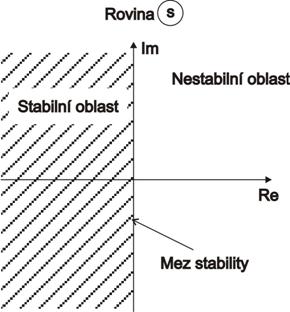
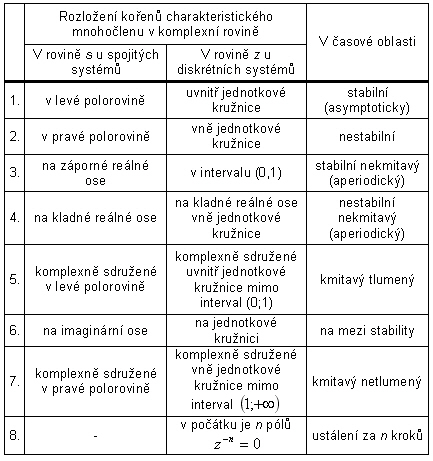
Kontrola stability regulačního obvodu spočívá v určení rozložení kořenů charakteristické rovnice v komplexní rovině kořenů (tab. 6. 1). Pokud lze kořeny vyčíslit, použijeme nutnou a postačující podmínku stability. Jinak je nutno použít pravidla, která umožní rozhodnout o stabilitě bez přímého výpočtu kořenů, tyto pravidla se nazývají kritéria stability [Balátě, 2003; Švarc, Šeda, Vítečková, 2007]. Tato kritéria budou, pospána v kapitolách 6. 3 a 6. 4.
6.1.2 Stabilita diskrétních systémů
Při vyšetřování stability diskrétních systémů se vychází opět z charakteristického mnohočlenu, resp. charakteristické rovnice (3. 14), která vystupuje ve jmenovateli všech základních přenosů regulačního obvodu.
Pro diskrétní regulační obvody je nutná a postačující podmínka stability formulována takto:
| Diskrétní regulační obvod je (asymptoticky) stabilní právě tehdy, když velikost všech kořenů charakteristického mnohočlenu bude menší než 1. |
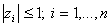 |
(6.3) |
Z nutné a postačující podmínky plyne, že stabilní oblast u diskrétních regulačních obvodů bude uvnitř jednotkové kružnice v oblasti komplexní proměnné z.
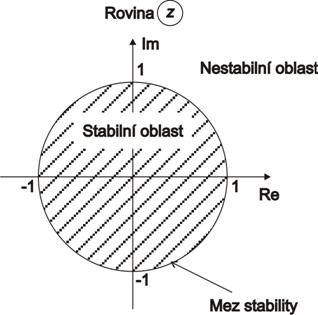
V tab. 6. 1 jsou vypsány stavy rozložení kořenů charakteristické rovnice, které mohou nastat při posuzování stability u spojitých a diskrétních systémů.
6.2 Bilineární transformace
U spojitých systémů bylo možno pro určování stability využít tzv. algebraická kritéria stability a kmitočtová kritéria stability. Hlavní výhodou těchto kritérií je, že dovolují určit stabilitu přímo z koeficientů charakteristické rovnice, aniž by bylo třeba určovat kořeny této rovnice.
Pro určení stability diskrétních systémů se zavádí tzv. bilineární transformace.
Bilineární transformace je definována vztahem
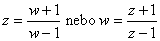 |
(6.4) |
Tato transformace zobrazí jednotkovou kružnici z komplexní roviny z na imaginární osu v komplexní rovině w. Vnitřek jednotkové kružnice z komplexní roviny z se převádí na levou polorovinu v komplexní rovině w.
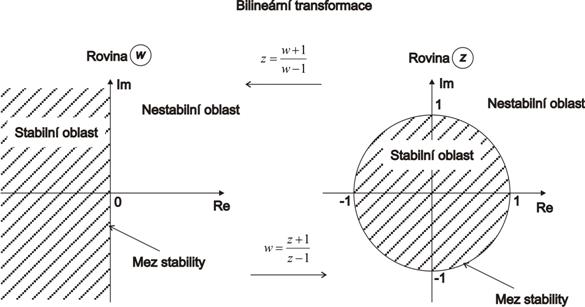
Pomocí bilineární transformace nahradíme v charakteristické rovnici proměnnou z za proměnnou w.
 |
(6.5) |
Po této úpravě dostaneme tzv. transformovanou charakteristickou rovnici 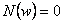 , pro kterou platí nutná a postačující podmínka spojitých regulačních obvodů, tj.
, pro kterou platí nutná a postačující podmínka spojitých regulačních obvodů, tj. 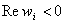 pro
pro 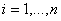 . Nyní můžeme pro charakteristický mnohočlen použít kritéria stability jako pro spojité systémy.
. Nyní můžeme pro charakteristický mnohočlen použít kritéria stability jako pro spojité systémy.
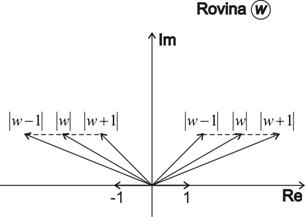
Správnost převodu jednotkové kružnice z komplexní roviny z na levou polorovinu v komplexní rovině w je možno prokázat jednoduchým důkazem.
- pokud vyjdeme z pravidla, že
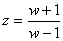 ,
, - dále platí podmínka stability diskrétních systémů, tzn.
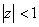 ,
, - dle předešlých bodů tedy platí, že
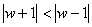 ,
, - nyní tedy můžeme dokázat na obr. 6. 5, že podmínka
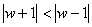 platí pro levou polorovinu komplexní roviny w (viz obr. 6. 5).
platí pro levou polorovinu komplexní roviny w (viz obr. 6. 5).
6.3 Algebraická kritéria stability
Kritéria stability umožňují rozhodnout o stabilitě systému bez výpočtů kořenů charakteristické rovnice. Nevýhodou těchto kritérií je, že nejdou aplikovat na systémy s dopravním zpožděním.
6.3.1 Routhovo-Schurovo kritérium stability
Toto kritérium, jak již bylo zmíněno, vychází z charakteristické rovnice, resp. charakteristického mnohočlenu, který je možno získat ze jmenovatele každého základního přenosu. Uvažujeme charakteristický mnohočlen po bilineární transformaci ve tvaru
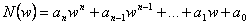 |
(6.6) |
U všech kritérií je nutno zkontrolovat Stodolovu nutnou podmínku stability, která zní: „Všechny koeficienty charakteristické rovnice musí existovat a musí mít stejné znaménko“, tj. 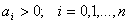 . Je-li charakteristický mnohočlen řádu
. Je-li charakteristický mnohočlen řádu 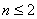 , nutná Stodolova podmínka přechází v nutnou a postačující podmínku stability.
, nutná Stodolova podmínka přechází v nutnou a postačující podmínku stability.
Postup při kontrole stability:
- koeficienty charakteristického mnohočlenu
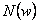 , resp. charakteristické rovnice napíšeme vedle sebe od nejvyšší mocniny,
, resp. charakteristické rovnice napíšeme vedle sebe od nejvyšší mocniny, - každý sudý koeficient podtrhneme,
- každý sudý koeficient násobíme podílem prvních dvou koeficientů a výsledek napíšeme o řádek níže posunutý o jednu pozici vlevo,
- novou řadu koeficientů odečteme od předcházející řady, díky této úpravě vypadne jeden koeficient,
- pokud jsou všechny koeficienty v nové řadě kladné, opakujeme stejný postup,
- pokud během výpočtu narazíme na nulový nebo záporný koeficient, můžeme říct, že diskrétní regulační obvod není stabilní,
- pokud dojdeme při výpočtu až ke stavu, kdy zůstanou pouze tři kladné koeficienty, můžeme říci, že charakteristická rovnice má všechny kořeny ve stabilní oblasti, tj. diskrétní regulační obvod je stabilní.
Příklad 6.1
Vyšetřete stabilitu diskrétního regulačního obvodu, je-li dán jeho charakteristický mnohočlen po bilineární transformaci, ve tvaru 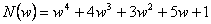 .
.
Řešení:
- Vypíšeme koeficienty charakteristického mnohočlenu od nejvyšší mocniny a podtrhneme každý sudý koeficient:
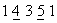
- Určíme podíl prvních dvou koeficientů:
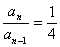
- Nyní můžeme provést samotnou kontrolu stability.
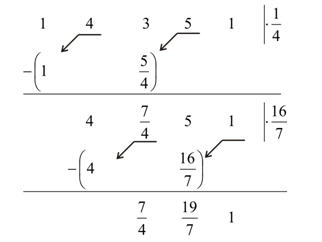
Během výpočtu jsme nenarazili na žádný záporný koeficient a koeficienty redukovaného mnohočlenu jsou kladné. Regulační obvod je tedy stabilní.
6.3.2 Hurwitzovo kritérium stability
Hurwitzovo kritérium stability opět vychází z charakteristického mnohočlenu, resp. charakteristické rovnice (6. 6). Uvažujeme charakteristický mnohočlen po bilineární transformaci. Opět je nutno kontrolovat Stodolovu podmínku stability.
Z koeficientů charakteristického mnohočlenu sestavíme tzv. Hurwitzovu matici (6. 7).
 |
(6.7) |
Hurwitzova matice  bude stejného řádu, jako je stupeň charakteristického mnohočlenu. Z Hurwitzovy matice sestavíme Hurwitzův determinant a z tohoto budeme určovat subdeterminanty, které jsou rovny hlavním rohovým minorům matice
bude stejného řádu, jako je stupeň charakteristického mnohočlenu. Z Hurwitzovy matice sestavíme Hurwitzův determinant a z tohoto budeme určovat subdeterminanty, které jsou rovny hlavním rohovým minorům matice  .
.
Hlavní rohové subdeterminanty tedy budou:
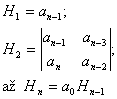 |
(6.8) |
Regulační obvod je (asymptoticky) stabilní právě tehdy, když všechny hlavní rohové subdeterminanty jsou kladné.
Pokud je některý ze subdeterminantů nulový nebo záporný, regulační obvod je nestabilní. Jestliže je koeficient charakteristické rovnice 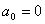 a všechny rohové subdeterminanty jsou kladné, regulační obvod je na nekmitavé mezi stability, tzn. charakteristická rovnice má nulový kořen. Pokud
a všechny rohové subdeterminanty jsou kladné, regulační obvod je na nekmitavé mezi stability, tzn. charakteristická rovnice má nulový kořen. Pokud 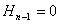 , regulační obvod je na kmitavé mezi stability, tzn. charakteristická rovnice má dvojici ryze imaginárních kořenů.
, regulační obvod je na kmitavé mezi stability, tzn. charakteristická rovnice má dvojici ryze imaginárních kořenů.
6.4 Kmitočtová kritéria stability spojitých regulačních obvodů
Pro kontrolu stability diskrétních regulačních obvodů použijeme jen jedno kmitočtové kritérium stability – Michajlovovo kritérium stability. Toto kritérium stability umožňuje rozhodnout o stabilitě na základě průběhu Michajlovova hodografu.
6.4.1 Michajlovovo kritérium stability
Vycházíme opět z transformovaného charakteristického mnohočlenu (6. 9), resp. transformované charakteristické rovnice.
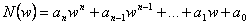 |
(6.9) |
Při využití tohoto kritéria vyhodnocujeme stabilitu dle průběhu koncového bodu Michajlovovy funkce 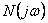 v komplexní rovině při měnící se frekvenci
v komplexní rovině při měnící se frekvenci 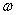 v rozsahu 0 až
v rozsahu 0 až 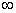 .
.
Michajlovovu funkci 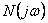 získáme dosazením
získáme dosazením
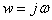 |
(6.10) |
do transformovaného charakteristického mnohočlenu 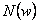 .
.
Z charakteristické funkce 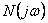 vyjádříme reálnou a imaginární část Michajlovovy funkce.
vyjádříme reálnou a imaginární část Michajlovovy funkce.
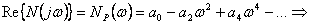 kořeny kořeny 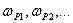 |
(6.11) |
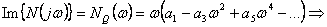 kořeny kořeny 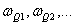 |
(6.12) |
a dosazením měnící se frekvence vykreslíme Michajlovovův hodograf.
Jestliže tedy leží všechny kořeny charakteristické rovnice v levé polorovině komplexní roviny, potom platí pro frekvenci 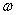 měnící se v rozsahu od 0 do
měnící se v rozsahu od 0 do 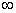
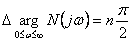 |
(6.13) |
Michajlovovo kritérium stability tedy zní:
| Regulační obvod je stabilní právě tehdy, když Michajlovovův hodograf bude začínat na kladné reálné poloose komplexní roviny a proti směru hodinových ručiček projde postupně tolika kvadranty, kolikátého stupně je charakteristický mnohočlen uzavřeného regulačního obvodu. |
Na obr. 6. 6 jsou zobrazeny Michajlovovy hodografy pro regulační obvody stabilní, nestabilní a na mezi stability.
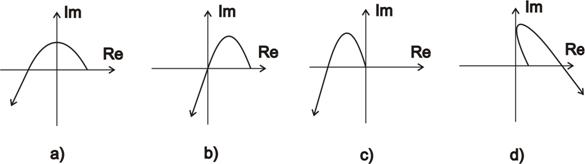
V případě Michajlovova kritéria můžeme také využít jeho analytickou formulaci. Určíme Michajlovovu funkci a její reálnou (6. 11) a imaginární část (6. 12) a vypočítáme kořeny reálné a imaginární části. Poté můžeme říci, že regulační obvod je stabilní pokud platí podmínka
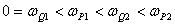 |
(6.14) |
tj. kořeny imaginární a reálné části se vzájemně střídají. Tato podmínka platí pro systémy bez dopravního zpoždění.
6.5 Řešené příklady
Příklad 6.2
Vyšetřete stabilitu regulačního obvodu, který je dán diskrétním přenosem řízení 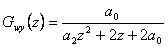 .
.
Řešení:
- Určíme charakteristický mnohočlen, resp. při položení rovno nule charakteristickou rovnici.
- Provedeme bilineární transformaci, tzn. za z dosadíme
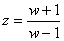 a získáme transformovaný charakteristický mnohočlen.
a získáme transformovaný charakteristický mnohočlen.
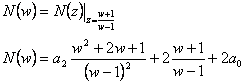
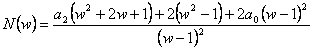
- Výraz položíme roven 0 a získáme charakteristickou rovnici.
- Provedeme úpravu a získáme tvar.
- Dále postupujeme stejně jako při kontrole stability dynamických systémů. Protože modifikovaný charakteristický mnohočlen je 2. stupně je Stodolova podmínka nutnou a postačující podmínkou stability.
- Aby systém byl stabilní, musí tedy platit:
- 1. podmínka:
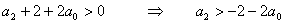
- 2. podmínka:

- 3. podmínka:
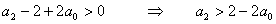
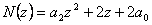
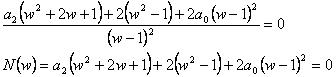
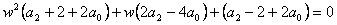
Na obr. 6. 7 je zobrazena stabilní oblast šrafovaná a ohraničená tučnými čarami dle vypočtených podmínek.
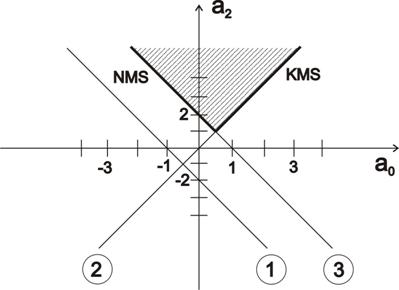
KMS označuje kmitavou mez stability, NMS označuje nekmitavou mez stability.
Příklad 6.3
Vyšetřete stabilitu regulačního obvodu pomocí Hurwitzova kritéria stability, který je dán diskrétním přenosem řízení
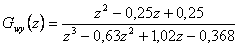 [Balátě, 2003].
[Balátě, 2003].
Řešení:
- Určíme charakteristický mnohočlen, resp. při položení rovno nule charakteristickou rovnici:
- Provedeme bilineární transformaci, tzn. za z dosadíme
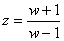 a získáme transformovanou charakteristickou rovnici.
a získáme transformovanou charakteristickou rovnici. - Po úpravě získáme transformovanou charakteristickou rovnici ve tvaru
- Provedeme kontrolu Stodolovy podmínky stability, která zní: Všechny koeficienty charakteristické rovnice musí existovat a musí mít stejné znaménko. Tuto kontrolu provádíme pro transformovanou charakteristickou rovnici.
- Nyní využijeme Hurwitzova kritéria kontroly stability.
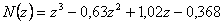
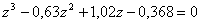
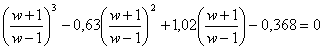
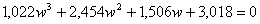
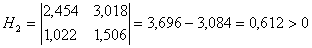
Hurwitzův determinant je kladný, tzn. diskrétní regulační obvod je stabilní.
Příklad 6.4
Vyšetřete stabilitu regulačního obvodu pomocí Michajlovova kritéria stability, jehož charakteristický mnohočlen je 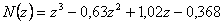 .
.
Řešení:
- Provedeme bilineární transformaci, tzn. za z dosadíme
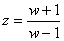 a získáme transformovanou charakteristickou rovnici.
a získáme transformovanou charakteristickou rovnici. - Po úpravě získáme transformovanou charakteristickou rovnici ve tvaru
- V charakteristickém mnohočlenu provedeme substituci
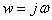 a získáme Michajlovovu funkci. Provedeme rozklad na reálnou a imaginární část charakteristické rovnice.
a získáme Michajlovovu funkci. Provedeme rozklad na reálnou a imaginární část charakteristické rovnice. - Provedeme rozklad na reálnou a imaginární část charakteristické rovnice.
- Nyní určíme kořeny reálné a imaginární části.
- Analyticky určíme stabilitu dle rovnice
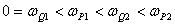
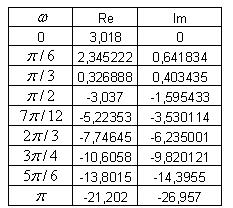
- Nyní můžeme vypočítat hodnoty reálné a imaginární části pro měnící se frekvenci
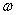 .
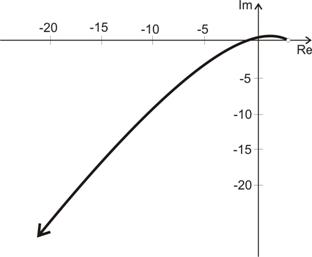
. - Nyní vykreslíme dle vypočtených hodnot Michajlovovův hodograf.
- Dle definice stability podle Michajlovova hodografu, můžeme říci, že diskrétní regulační obvod je stabilní.
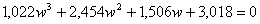
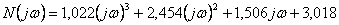
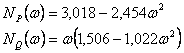

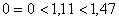
Podmínka stability je splněna a tudíž diskrétní regulační obvod je stabilní.