Eulerovské tahy
Eulerovský tah je takový tah, který obsahuje všechny hrany právě jednou. Orientované grafy obsahují orientované tahy a neorientované grafy obsahují neorientované tahy [Demel, J., 1982], [Plesník, J., 1983].
· Uzavřené Eulerovské tahy jsou takové tahy, u kterých je počáteční a koncový uzel totožný.
· Neuzavřené Eulerovské tahy jsou takové tahy, které nemají totožný počáteční a koncový uzel.
“Jednotažky“ jsou všechny hrany nakresleny jedním tahem.
|
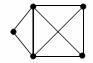
Obr. 3.6 Neuzavřená jednotažka |
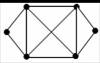
Obr. 3.7 Uzavřená jednotažka |
Typy úloh
- Rozhodnout, zda v daném grafu existuje otevřený nebo uzavřený Eulerovský tah.
- V daném grafu sestrojit otevřený nebo uzavřený Eulerovský tah.
- V daném grafu najít nejmenší počet tahů, nikoli Eulerovských, které pokrývají všechny hrany grafu.
- V daném souvislém grafu (mezi každými dvěma uzly existuje hrana), jehož hrany jsou ohodnoceny kladnými čísly, máme za úkol najít nejkratší uzavřený sled, který obsahuje každou hranu alespoň jednou. Obecně nazývána Úloha čínského pošťáka.
Věta 1:
Nechť graf G je neorientovaný, pak v grafu existuje neorientovaný uzavřený Eulerovský tah právě tehdy, když každý uzel grafu je sudého stupně.
Věta 2:
Nechť graf G je orientovaný, pak v grafu G existuje orientovaný uzavřený Eulerovský tah právě tehdy, když pro každý uzel grafu platí, že počet hran vstupujících do uzlu je roven počtu hran z uzlu vystupujících.
Algoritmus pro hledání uzavřeného Eulerovského tahu
Musí být zajištěna platnost věty 1 nebo 2. V algoritmu se pak střídavě prodlužují dvě fáze:
· Existující tah prodlužujeme, dokud se nestane uzavřeným.
· Uzavřený tah kontrolujeme, zda je Eulerovský. Při kontrole procházíme podél tahu a v každém uzlu x testujeme, zda v okolí uzlu x existuje hrana, která dosud neleží v tahu. Jestliže ano, pak přerušíme kontrolu, tah v uzlu x rozpojíme a začneme jej prodlužovat. Prodlužování skončí v uzlu x. Po rozpojení nového a starého tahu pokračujeme v kontrole počínaje uzlem x a postupujeme podél nové části tahu. Takto je zajištěno, že jak při prodlužování, tak i při kontrole postupujeme podél každé hrany pouze jednou. Celý postup je tedy velmi rychlý.
Věta 3:
Nechť G je neorientovaný souvislý graf, který obsahuje k uzlů lichého stupně, pak nejmenší počet neorientovaných tahů pokrývajících všechny hrany grafu je k/2.
Počet uzlů lichého stupně v grafu (obr. 3.10): k = 4 Þ 2 tahy.
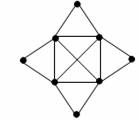
Obr. 3.10 Graf potvrzující větu 3
Věta 4:
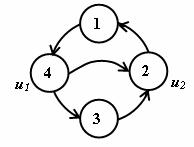
V souvislém orientovaném grafu je právě jeden Eulerovský tah neuzavřený právě tehdy, když graf je souvislý a existují-li v něm dva uzly u1, u2, pro které platí (viz obr. 3.11):
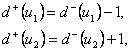
kde je: d + ( u1) - počet hran vstupujících do uzlu u1,
d - ( u2) - počet hran vystupujících z uzlu u2.
Pak uzel u1
je počáteční uzel a uzel u2
je koncový uzel neuzavřeného Eulerovského tahu. Pro ostatní uzly platí d+(u) = d -(u).
|
|
u1 = 4 – 3 – 2 – 1 – 4 – 2 = u2 |
Obr. 3.11 Graf potvrzující větu 4
Algoritmus čínského pošťáka
Pošťák musí při roznášce pošty alespoň jedenkrát projít každou ulicí svého rajónu. Jak má postupovat, aby ušel co nejméně kilometrů, to znamená, aby kratší cesty procházel vícekrát [Demel, J., 1982]?
1. Zjistit, zda jsou všechny uzly sudého stupně.
2. Není-li tomu tak, musíme přidat hrany, abychom tuto podmínku splnili a to provedeme tak, že spojíme uzly s lichým stupněm nejkratší cestou.
3. Provedeme kontrolu, zda cesta pošťáka je opravdu nejkratší.
Zde jsou příklady na procvičení probrané látky. Eulerovské tahy.