Příklad 3.1

Máme město, které se rozkládá na dvou ostrovech a dvou březích, které jsou spojeny sedmi mosty. Naším úkolem je určit, zda je možno projít přes každý ze sedmi mostů přesně jednou, aniž bychom přeplavali řeku (viz obr. 3.8)?

Obr. 3.8 Sedm mostů a dva břehy daného města a odpovídající graf

Není možno projít přes každý most bez přeplavání řeky právě jednou, protože všechny uzly mají lichý stupeň.

Příklad 3.2

Sestrojme uzavřený orientovaný Eulerovský tah (viz obr. 3.9) pomocí výše uvedeného postupu.

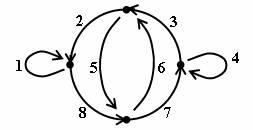
Obr. 3.9 Graf k příkladu 3.2

Podle algoritmu pro hledání uzavřeného Eulerovského tahu je pro graf na obr. 3.9 sled hran uzavřeného tahu: 1 – 8 – 7 – 4 – 3 – 2. Při kontrole zjistíme, že v uzlu, ve kterém končí hrana 8 vychází hrana 6 a vstupuje hrana 5, takže Eulerovský tah upravíme 1 – 8 – 6 – 5 – 7 – 4 – 3 – 2.

Příklad 3.3

Řešme úlohu čínského pošťáka pro graf na  obr. 3.12.

Řešení:

Hrany tvořící nejlevnější perfektní párování jsou označeny tučně (viz obr. 3.13). Stupně všech jeho uzlů jsou sudé, nečiní tedy potíže nalézt v tomto grafu uzavřený Eulerovský tah.

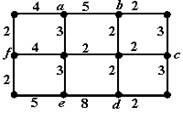
Obr. 3.12 Graf k úloze čínského pošťáka – příklad 3.3

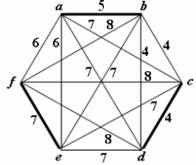
Obr. 3.13 Hrany tvořící nejlevnější perfektní párování – tučné hrany