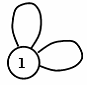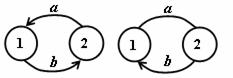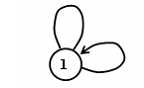Teorie grafů
Teorie grafů patří mezi relativně mladé matematické disciplíny. Jedná se o obor matematiky, pomocí něhož lze formulovat a řešit mnoho problémů z různých oblastí, nejčastěji celočíselné a kombinatorické povahy [Demel, J., 1988], [Sedláček, J., 1981].
Základní pojmy
Graf je určitý útvar (systém), který je možno znázornit obrázkem v rovině pomocí bodů (uzly grafu) a spojnic mezi body (hrany grafu).
Orientovaný graf je trojice G = (V, E, e) tvořená konečnou množinou prvků V, jejíž prvky nazýváme uzly, konečnou množinou E, jejíž prvky nazýváme orientovanými hranami a zobrazením e : E ® V2, které nazýváme vztahem incidence, a které přiřazuje každé hraně e Î E uspořádanou dvojici uzlů.
Neorientovaný graf je trojice G = (V, E, e) tvořená konečnou množinou V, jejíž prvky nazýváme uzly, konečnou množinou E, jejíž prvky nazýváme neorientovanými hranami a zobrazením e (vztah incidence), které přiřazuje každé hraně e jedno nebo dvouprvkovou množinu uzlů.
Cesta v grafu je posloupnost orientovaných hran, při které vždy následující hrany začínají v uzlu, v němž končí předcházející hrana.
Cyklus (kružnice u neorientovaného grafu) je taková cesta, která začíná a končí v témže uzlu.
Řetěz je cesta bez ohledu na orientaci grafu.
Souvislý
graf je graf, u kterého mezi všemi dvojicemi uzlů existuje alespoň jedna
cesta.
Nesouvislý
graf je graf, u kterého neexistuje alespoň jedna cesta mezi všemi dvojicemi
uzlů.
Strom je takový graf, který neobsahuje žádný cyklus.
Podgraf původního grafu je graf, který vznikne tím, že vynecháme z grafu některé uzly a příslušné hrany těchto uzlů.
Acyklický graf je graf, který neobsahuje žádný cyklus.
Ohodnocený graf (orientovaný, neorientovaný) je graf, ve kterém reálná funkce definovaná na množině hran přiřazuje každé hraně nějakou hodnotu (například vzdálenost, doba, energie…).
Síť
je graf, který je konečný, souvislý, orientovaný, acyklický a ohodnocený,
v němž existuje jeden konečný a jeden počáteční uzel.
Konečný graf má konečný počet uzlů a hran.
Řezem sítě se nazývá množina všech hran, které spojují uzly množiny U1 s uzly množiny U2, kdy U1 je množina uzlů, která obsahuje počáteční uzel a všechny uzly dosažitelné z počátečního uzlu po nenasycené cestě. Množina uzlů U2 je taková množina, která obsahuje koncový uzel a všechny zbývající uzly.
Kapacita řezu je číslo, které je tvořeno součtem kapacit (ohodnocení) všech hran řezu.
Minimální řez je řez, který má nejmenší kapacitu.
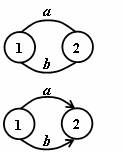
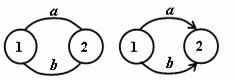
Multigraf je graf, v němž mezi některou dvojicí uzlů existuje v jednom směru větší počet hran než jedna.
Druhy hran:
Tabulka 3.1 Druhy hran
|
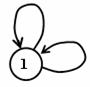
Smyčky |
|
Hrana, která inciduje s jedním uzlem |
|
Rovnoběžné hrany |
|
Incidují se stejnými uzly. |
|
Orientované hrany |
|
Je naznačen směr orientace |
|
Neorientované hrany |
|
|
|
Násobné hrany |
|
Jsou rovnoběžné hrany, které jsou buď neorientované nebo všechny souhlasně orientované. |
Tabulka 3.2 Rozdělení hran a smyček
|
|
ROVNOBĚŽNÉ |
|
|
HRANY |
SMYČKY |
|
|
Násobné |
|
|
|
Nenásobné |
|
|
Klasifikace grafů:
a) Podle hran:
· jednoduchý graf (orientovaný, neorientovaný) je graf, který obsahuje prosté hrany bez smyček.
· prostý graf (orientovaný, neorientovaný) je graf, v němž násobnost každé hrany je nejvýše rovna jedné (neobsahují násobné hrany),
· multigraf (orientovaný, neorientovaný) je graf, v němž násobnost alespoň jedné hrany je větší než jedna (obsahují násobné hrany),
Tabulka 3.3 Typ grafu podle hran
|
TYP GRAFU |
NEORIENTOVANÝ |
ORIENTOVANÝ |
|
Jednoduchý graf |
|
|
|
Prostý graf |
|
|
|
Multigraf |
|
|
b) Podle počtů hran a uzlů:
· konečný graf (konečný počet hran a uzlů),
· nekonečný graf (nekonečný počet hran a uzlů),
· prázdný graf (prázdná množina uzlů a hran).
Úplný graf je graf, mezi jehož každými dvěma různými uzly existuje právě jedna hrana, pak platí
![]()
kde je:
n - počet uzlů
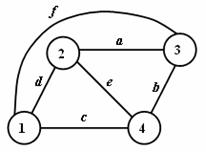
Obr. 3.1 Příklad úplného grafu
Podgraf – graf G´
je podgrafem grafu G, jestliže V´Í V, E´Í E
a ![]() je zúžením zobrazení
je zúžením zobrazení
![]() pro graf G´,
pro graf G´,
kde grafy G´=
(V´, E´, ![]() ),
),
G = (V,
E, ![]() ),
),
jsou buď oba orientované nebo oba neorientované.
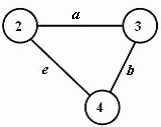
Obr. 3.2 Podgraf úplného grafu z obrázku. 3.1
Faktor grafu –
graf G´ je faktorem grafu G, jestliže graf G´je podgrafem
grafu G, který má stejnou množinu uzlů (V´ = V) a jeho
množina hran E´ je podmnožinou množiny hran E ![]() .
.
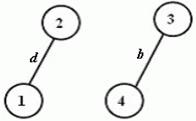
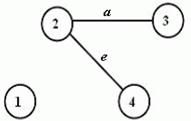
Obr. 3.3 Faktory úplného grafu z obrázku 3.1
Stupeň uzlu je počet hran incidujících s daným uzlem (smyčka se počítá dvakrát).
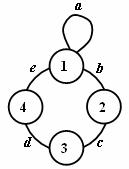
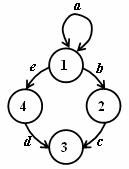
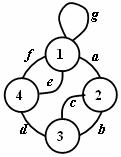
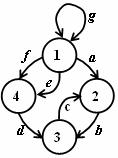
Přesuny z jednoho uzlu do druhého uzlu
Sled je uspořádaná posloupnost uzlů a hran (uzly a hrany se mohou opakovat).
S1 = (
S2 = (
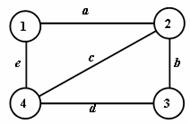
Obr. 3.4 Přesuny uzlů
Délka sledu: l(S1) = a + b + d + e
l(S2) = a + c + e
počáteční uzel = koncový uzel Þ uzavřený sled
počáteční uzel ¹ koncový uzel Þ otevřený sled
Násobnost hrany – počet výskytů téže hrany v určitém sledu.
Tah je sled, v němž se žádná hrana nevyskytuje více než jednou.
Cesta je takový tah, v němž se každý uzel vyskytuje jen jednou.
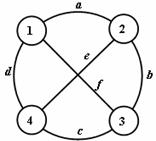
Kružnice je uzavřená cesta (viz obr. 3.5).
Obr. 3.5 Kružnice – uzavřená cesta