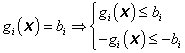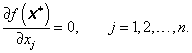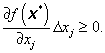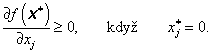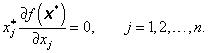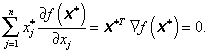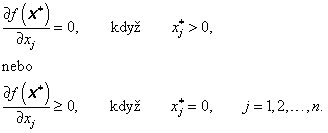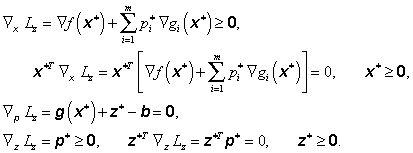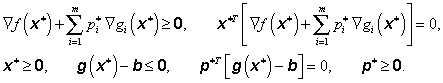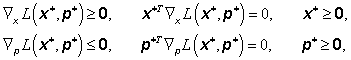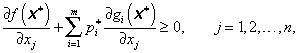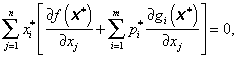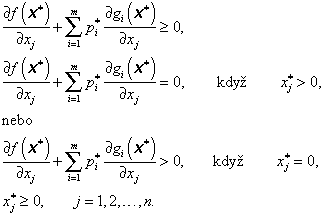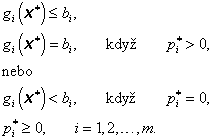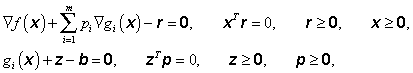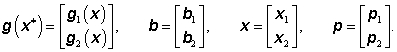3 Statická optimalizace funkcí více proměnných
3.3 Optimalizační úlohy s omezeními ve tvaru nerovnosti
Optimalizační úlohy s omezeními ve tvaru nerovnosti (neklasické úlohy na vázaný extrém, úlohy nelineárního programování) lze vyjádřit ve tvaru
|
(3.66) |
Na rozdíl od optimalizačních úloh s omezeními ve tvaru rovností (3.20), veličiny n a m mohou být libovolná konečná čísla. Zvolený typ nerovnosti 
ve vztahu na množinu přípustných řešení X lze získat z opačné nerovnosti vynásobením -1 a z rovnosti – pomocí dvou nerovností, např.:
|
(3.67) |
|
(3.68) |
Omezení vyjadřující nezápornost proměnných {xj} rovněž nejsou podmínkou. Může-li nějaká proměnná nabývat jak kladných, tak i záporných hodnot, např. xj pak tuto proměnnou zastoupíme dvěma pomocnými proměnnými 
a 
, které vyhovují vztahům
|
(3.69) |
Nově formulovaná optimalizační úloha nebude obsahovat proměnnou xj.
Podmínky nezápornosti
|
(3.70) |
vytvářejí v n-rozměrném euklidovském prostoru nezáporný ortant. V R2 je to nezáporný kvadrant a v R3 – nezáporný oktant.
Uvažujme nejdříve optimalizační úlohu pouze při podmínkách nezápornosti (3.70), tj.
|
(3.71) |
Má-li účelová funkce f(x) v bodě 
lokální minimum a spojité parciální derivace druhého řádu, pak podobně jako v případě úlohy bez omezení musí pro 
platit základní nerovnost [viz (3.4) až (3.8)]
|
(3.72) |
Základní nerovnost (3.72) vyjadřuje nutnou podmínku existence lokálního minima účelové funkce f( x) v bodě x*. Je-li x* > 0, tzn. x* je vnitřním bodem množiny X, pak základní nerovnost (3.72) platí pro všechny směry (přírůstky) 
a tedy nutná podmínka prvního řádu, podobně jako v případě úlohy bez omezení, má tvar [viz (3.10)]
|
(3.73) |
Předpokládejme nyní, že v optimálním bodě x* jedna proměnná nabývá hraniční hodnoty, tj. např. 
. Nechť přírůstky všech zbývajících proměnných jsou nulové, pak jediný přípustný směr je takový, pro který 
. Ze základní nerovnosti (3.72) tedy vyplývá
|
(3.74) |
Proto nutná podmínka prvního řádu spočívá v tom, že
|
(3.75) |
V bodě vnitřního minima 
parciální derivace prvního řádu podle xj je nulová (obr. 3.3a) a v bodě hraničního minima 
parciální derivace prvního řádu podle xj je větší, nebo rovna nule (obr. 3.3b,c). Tzn. buď parciální derivace prvního řádu je nulová (ve vnitřním bodě) nebo odpovídající proměnná je nulová (v hraničním bodě), proto jejich součin v bodě lokálního minima x* je vždy roven nule
|
(3.76) |
Protože všechny proměnné {xj} jsou nezáporné, součet součinů (3.76) musí být rovněž nulový, tj.
|
(3.77) |
Ze vztahů (3.73) – (3.77) vyplývá, že v bodě x* lokálního minima účelové funkce f(x) musí být splněno 2n + 1 nutných podmínek prvního řádu
|
(3.78) |
resp.
|
(3.79) |
Pro jednorozměrnou optimalizační úlohu všechny možné případy ilustruje obr. 3.3.
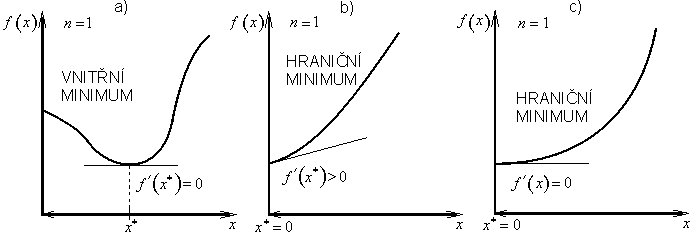 Obr. 3.3: Minima funkce pro jednorozměrnou optimalizaci |
Vztahy (3.73), resp. (3.79) využijeme pro řešení obecné optimalizační úlohy s omezeními ve tvaru nerovností (3.66).
Zavedeme nezáporný vektor pomocných proměnných
|
(3.80) |
pomocí kterého omezující nerovnosti
|
(3.81) |
lze napsat jako rovnosti
|
(3.82) |
Nyní optimalizační úlohu (3.66) můžeme zapsat ve tvaru
|
(3.83) |
při omezujících podmínkách
|
(3.84) |
Nezápornost pomocných proměnných zajišťuje splnění omezení ve tvaru nerovností (3.81). Kdyby omezující podmínky (3.84) neobsahovaly n + m podmínek nezápornosti, pak tato úloha by mohla být vyřešena Lagrangeovou metodou. Lagrangeova funkce takové úlohy může být vyjádřena vztahem
|
(3.85) |
kde p = [p1, p2, ..., pm]T je vektor Lagrangeových multiplikátorů.
Nutné podmínky prvního řádu pro tuto úlohu by spočívaly v tom, že všechny parciální derivace prvního řádu funkce Lx(x, p, z) podle x, p a z by měly být nulové. Protože x a z jsou nezáporné vektory, odpovídající podmínky na hodnoty parciálních derivací prvního řádu funkce Lx(x, p, z) podle těchto n + m proměnných se změní na podmínky, které lze obdržet ze vztahů (3.78), tj.
|
(3.86) |
Po zastoupení vektoru pomocných proměnných z vztahem (3.82) a úpravě dostaneme Kuhnovy-Tuckerovy nutné podmínky prvního řádu pro existenci lokálního řešení úlohy (3.66):
|
(3.87) |
Tytéž podmínky lze obdržet pomocí (zobecněné) Lagrangeovy funkce, kterou pro výchozí optimalizační úlohu (3.66) vyjádříme vztahem
|
(3.88) |
Pak Kuhnovy-Tuckerovy podmínky (3.87) můžeme zapsat v jednoduchém symetrickém tvaru
|
(3.89) |
resp. po rozepsání jako 2n + 2m + 2 podmínek
|
(3.90) |
|
(3.91) |
|
(3.92) |
|
(3.93) |
|
(3.94) |
|
(3.95) |
Kuhnovy-Tuckerovy podmínky jsou nutné a postačující pro (ostré) globální minimum za předpokladu, že účelová funkce f(x) je (ryze) konvexní a že omezující funkce {gi(x)} jsou konvexní a splňují určitou podmínku regularity (bude uvedena později). V tomto případě hovoříme o konvexním programování.
Vztahy (3.92) a (3.93) vyjadřují podmínky nezápornosti a omezující nerovnosti pro výchozí optimalizační úlohu (3.66). Díky nerovnostem (3.90) a (3.92) každý sčítanec součtu (3.91) musí být nulový, protože buď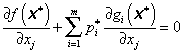 
nebo xj = 0 nebo obě rovnosti jsou splněny současně (j = 1, 2, …, n). Platí tedy vztahy:
|
(3.96) |
Podobně každý sčítanec součtu (3.94) musí být roven nule, protože buď gi( x*) – bi = 0 nebo 
, nebo obě rovnosti jsou splněny současně (i = 1, 2, …, m).
Platí tedy
|
(3.97) |
Podmínky (3.96) a (3.97) vyjadřují jinou formulaci Kuhnových-Tuckerových podmínek.
Hodnota Lagrangeovy funkce L( x, p) v optimálním bodě [x*, p*]T je rovna optimální hodnotě účelové funkce f *, tj.
|
(3.98) |
protože 
Nerovnosti, které v optimálním bodě x* jsou splněny jako rovnosti, se nazývají aktivní.
Ukážeme si geometrickou interpretaci Kuhnových-Tuckerových podmínek. Uvažujme tyto podmínky ve tvaru (3.86). Zavedeme-li další vektor pomocných proměnných
|
(3.99) |
pak podmínky (3.86) budou mít tvar
|
(3.100) |
kde všechny proměnné, funkce a derivace jsou uvažovány pro x = x*, p = p*, r = r* a z = z*. Nezápornost pomocných proměnných zaručuje splnění odpovídajících nerovností. Prvních n vztahů lze napsat ve tvaru:
|
(3.101) |
kde I je čtvercová jednotková matice řádu n.
Geometrický význam vztahu (3.101) spočívá v tom, že v optimálním bodě x* záporný gradient (antigradient) účelové funkce je dán lineární kombinací gradientů aktivních omezujících nadploch (obr. 3.4). Gradienty omezujících funkcí 
jsou trasponované řádky příslušné Jacobiovy matice [viz vztah (3.51)] a gradienty podmínek nezápornosti jsou řádky jednotkové matice I. Váhovými koeficienty jsou nezáporné Lagrangeovy multiplikátory 
a pomocné proměnné 
. Odtud vyplývá, že neregulární (singulární) omezení budou taková aktivní omezení, jejichž gradienty jsou lineárně závislé, jak je to ukázáno na obr. 3.5, kde omezující funkce tvoří jakési ostří.
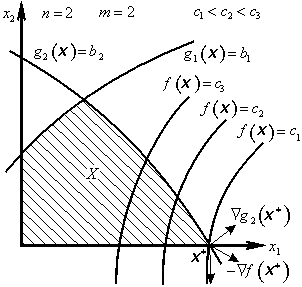 Obr. 3.4: Aktivní omezující nadplochy |
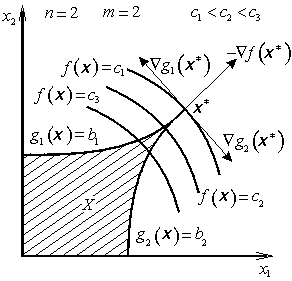 Obr. 3.5: Lineárně závislé gradienty |
Jsou-li omezující funkce {gi(x)} konvexní, pak omezení budou regulární (podle Slatera), bude-li existovat takový bod 
, pro který platí
|
(3.102) |
V případě lineárních omezujících funkcí {gi(x)} podmínky regularity jsou vždy splněny.
Porovnáme-li Kuhnovy-Tuckerovy podmínky (3.89) s podmínkami (3.78), uvidíme, že bod [ x*, p*]T je sedlovým bodem Lagrangeovy funkce L(x, p), tzn., že minimalizuje Lagrangeovu funkci podle všech nezáporných proměnných x a maximalizuje podle všech nezáporných Lagrangeových multiplikátorů p, tj.
|
(3.103) |
při všech 
a 
.
Úloha získání nezáporných vektorů x* a p * vyhovujících nerovnostem (3.103) se nazývá úloha na sedlový bod.
Nyní již můžeme zformulovat Kuhnovu-Tuckerovu větu (větu o sedlovém bodě):
„Bod 
je řešením optimalizační úlohy (3.66), tj. 
, tehdy a jen tehdy, existuje-li takový bod 
, že platí nerovnost (3.103), tj. 
, 
“.
Pro spojitě diferencovatelné funkce f(x), {gi( x)} a regulární omezení vztahy (3.89) a (3.103) jsou navzájem ekvivalentní, tj. optimalizační úlohu lze zastoupit ekvivalentní úlohou na sedlový bod.
Skutečnost, že bod [ x*, p*]T je sedlovým bodem Lagrangeovy funkce L(x, p) a že dvě soustavy podmínek (3.89) jsou symetrické, přirozeným způsobem vede k duálním (sdruženým) úlohám:
|
(3.104) |
a
|
(3.105) |
Úloha (3.104) se nazývá primární (přímá) a úloha (3.105) – duální (sdružená). V duální optimalizační úloze jako nezávisle proměnné vystupují Lagrangeovy multiplikátory p.
V optimalizačních úlohách s omezeními ve tvaru nerovností Lagrangeovy multiplikátory mohou být rovněž využity jako charakteristiky citlivosti optimální hodnoty účelové funkce ke změnám hodnot omezujících konstant, podobně jako v úlohách s omezeními ve tvaru rovností.
Kdyby bylo známo, která omezení jsou aktivní, která neaktivní a které proměnné jsou nulové, bylo by možné Kuhnovy-Tuckerovy podmínky zapsat ve tvaru rovností. Předpokládejme např., že omezující funkce {gi(x)} a proměnné {xi} jsou očíslovány tak, že v optimálním bodě x * prvních 
nerovností je splněno jako rovnosti (jsou aktivní) a zbývajících m - m1 – jako ostré nerovnosti (jsou neaktivní) a že prvních 
proměnných je kladných a zbývajících n - n1 nulových, pak lze psát
|
(3.106) |
kde vektory g1( x), b1 a p1 jsou tvořeny prvními m1 prvky vektorů g(x), b, p a vektor x1 je tvořen prvními n1 prvky vektoru x.
Pak Kuhnovy-Tuckerovy podmínky (3.89) mohou být zapsány ve tvaru
|
(3.107) |
Pro posledních m - m1 Lagrangeových multiplikátorů p2 platí [viz poslední rovnice ve vztahu (3.107)]
|
(3.108) |
Posledních m - m1 omezení je neaktivních. Tato omezení jsou splněna jako ostré nerovnosti, proto malé změny hodnot odpovídajících omezujících konstant nemohou změnit optimální hodnotu účelové funkce.
Pro prvních m1 Lagrangeových multiplikátorů p1 obecná optimalizační úloha s omezeními ve tvaru nerovností se změní na klasickou optimalizační úlohu s omezeními ve tvaru rovností
|
(3.109) |
Proto při předpokladu, že proměnné x1 a p1 jsou funkcemi b1, derivováním Lagrangeovy funkce podle b1 dostaneme [viz (3.44) – (3.47), (3.60) – (3.62)]
|
(3.110) |
Příklad 3.3
Je třeba řešit optimalizační úlohu
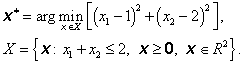
Řešení:
Sestavíme Lagrangeovu funkci
a napíšeme Kuhnovy-Tuckerovy podmínky
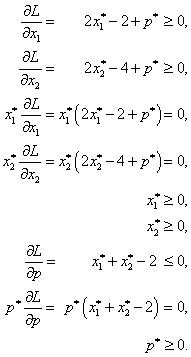
Při vyhledávání proměnných x* a p* vyhovujících Kuhnovým-Tuckerovým podmínkám, je nejlépe začít od řešení rovností a pak kontrolovat splnění nerovností pomocí tabulky (viz níže).
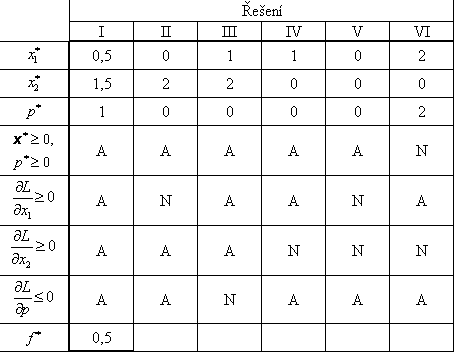 A – vyhovuje, N – nevyhovuje |
Účelová funkce je ryze konvexní a omezující funkce je lineární, proto Kuhnovy-Tuckerovy podmínky jsou nutné a postačující. V bodě 
a 
musí tedy nutně vystupovat jednoznačné ostré globální minimum f * = 0,5.
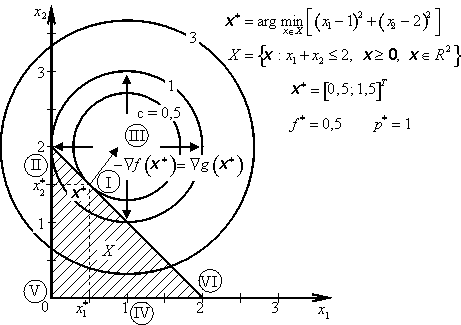 Příklad 3.3 |
Příklad 3.4
Určete globální minimum účelové funkce 
při omezeních 
Řešení:
Minimalizační úloha má tvar
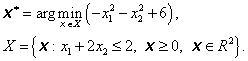
Sestavíme Lagrangeovu funkci
a napíšeme Kuhnovy-Tuckerovy podmínky:
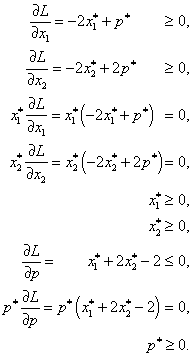
Podobně jako v příkladu 3.3 sestavíme tabulku řešení rovnosti a zkontrolujeme splnění nerovností.
Protože účelová funkce je ryze konkávní a hledáme globální minimum, Kuhnovy-Tuckerovy podmínky je třeba považovat pouze za nutné podmínky pro existenci lokálního minima.
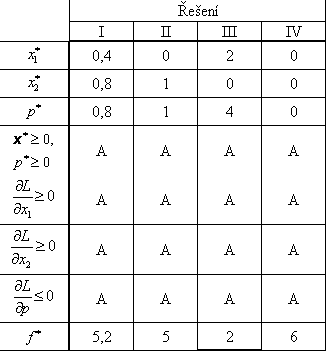 A – vyhovuje, N – nevyhovuje |
Kuhnovy-Tuckerovy podmínky jsou splněny ve všech případech a proto srovnáním funkčních hodnot vyčleníme globální minimum. Vystupuje v optimálním bodě x* = [2, 0]T. Optimální hodnota účelové funkce je f * = 2.
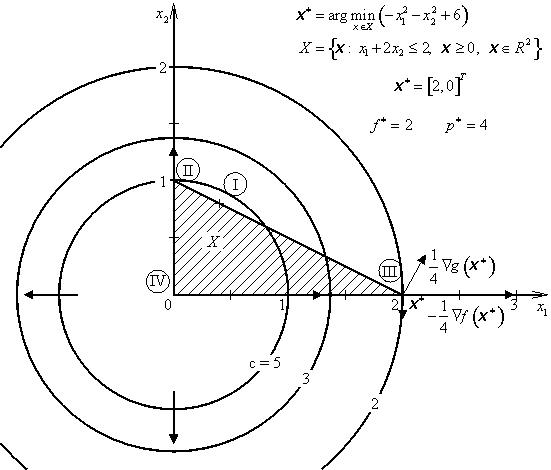 Příklad 3.4 |
Příklad 3.5
Vyřešíme optimalizační úlohu
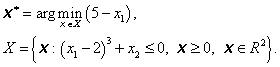
Protože optimalizační úloha je velmi jednoduchá, je zřejmé, že účelová funkce nebývá f *= 3 v optimalizačním bodě x* = [2, 0]T Zkontrolujeme, zda v tomto bodě budou splněny Kuhnovy-Tuckerovy podmínky.
Sestavíme Lagrangeovu funkci
a napíšeme Kuhnovy-Tuckerovy podmínky:
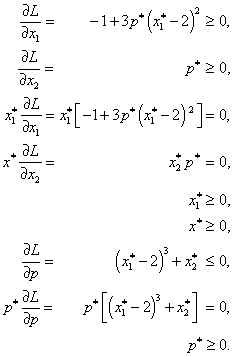
V optimalizačním bodě x* = [2, 0]T Kuhnovy-Tuckerovy podmínky nejsou splněny, protože omezení jsou neregulární. Gradienty omezení jsou lineárně závislé, a proto záporný gradient účelové funkce nemůže být vyjádřen jako lineární kombinace gradientů aktivních omezení.
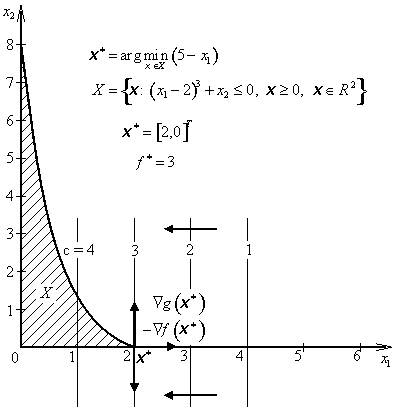 Příklad 3.5 |