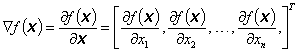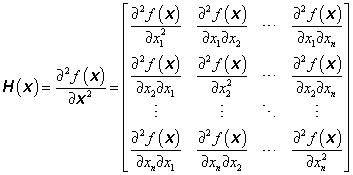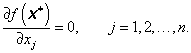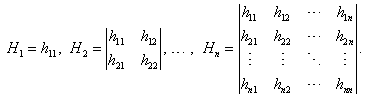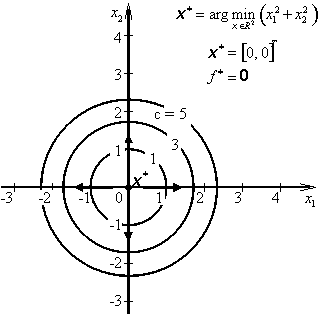3 Statická optimalizace funkcí více proměnných
3.1 Optimalizační úlohy bez omezení
Optimalizační úlohy bez omezení (úlohy na volný extrém, úlohy bez vazebních podmínek) mohou být zapsány ve tvaru
|
(3.1) |
resp.
|
(3.2) |
kde
|
(3.3) |
Má-li účelová funkce f(x) v bodě x* lokální minimum, pak ve shodě s (1.31) platí
|
(3.4) |
kde h je libovolné malé kladné číslo 
, 
– přírůstek vektoru x, který v euklidovském prostoru Rn vyjadřuje směr.
Funkci vystupující na pravé straně nerovnosti (3.4) rozložíme v okolí bodu h = 0 podle Taylorova vzorce se zbytkem v Lagrangeově tvaru (1.30)
|
(3.5) |
kde 0 < a < 1 a
|
(3.6) |
je gradient účelové funkce f(x),
|
(3.7) |
je Hessova matice (hessián) parciálních derivací druhého řádu účelové funkce f(x).
Z nerovností (3.4) a (3.5) po úpravě dostaneme tzv. základní nerovnost
|
(3.8) |
která musí být splněna pro všechny směry 
a libovolné malé kladné číslo h. Proto po vydělení obou stran této nerovnosti číslem h a limitním přechodu 
dostaneme
|
(3.9) |
Tato podmínka říká, že v bodě lokálního minima účelové funkce f(x) všechny její parciální derivace prvního řádu jsou nulové, tj.
|
(3.10) |
Bod x * vyhovující podmínkám (3.9) nebo (3.10) je stacionárním bodem (kritickým bodem).
Ze základní nerovnosti (3.8) a nutné podmínky prvního řádu (3.9) vyplývá nutná podmínka druhého řádu
|
(3.11) |
Pomocný materiál
Je-li H = [hij] symetrická čtvercová matice řádu n, pak výraz
|
(3.12) |
se nazývá kvadratická forma.
Kvadratická forma (3.12) je:
a) kladně, resp. záporně definitivní, když pro všechny nenulové vektory 
platí 
, resp. 
;
b) kladně, resp. záporně semidefinitivní, když pro všechny vektory platí 
, resp. 
a existuje-li takový vektor , že 
;
c) indefinitivní, když není kladně ani záporně (semi-) definitivní.
Shodně a kvadratickou formou 
nazýváme i jí příslušnou matici H kladně, resp. záporně (semi-) definitní, resp. indefinitní.
Definitnost symetrických čtvercových matic a jim příslušných kvadratických forem lze poměrně snadno určit pomocí Sylvestrova kritéria. Symboly H1, H2, …, Hn označíme hlavní rohové minory (subdeterminanty) matice H, tj.
|
(3.13) |
„Kvadratická forma (3.12) a jí příslušná matice H jsou kladně definitní 
, když všechny její hlavní rohové minory (3.13) jsou kladné, tj.
|
(3.14) |
Kvadratická forma (3.12) a jí příslušná matice H jsou kladně semidefinitní 
, když všechny její hlavní (a tedy nejenom rohové) minory jsou nezáporné a přitom alespoň jeden z hlavních rohových minorů je roven nule“.
Z uvedených vlastností kvadratických forem přímo vyplývá, že je-li matice H kladně (semi-) definitní, pak matice –H je záporně (semi-) definitní a naopak.
Nutná podmínka druhého řádu (3.11) říká, že má-li účelová funkce f(x) v bodě lokální minimum, pak Hessova matice v tomto bodě musí být kladně semidefinitní (účelová funkce f(x) musí být v okolí bodu x* konvexní), tj.
|
(3.15) |
Postačujícími podmínkami pro to, aby účelová funkce f(x) měla v bodě x* ostré lokální minimum tj.
|
(3.16) |
jsou
|
(3.17) |
Postačující podmínky (3.17) vyžadují kladnou definitnost Hessovy matice ve stacionárním bodě (účelová funkce f(x ) musí být v okolí bodu x* ryze konvexní).
Je-li ve stacionárním bodě x* Hessova matice záporně definitní, tj.
|
(3.18) |
pak jsou splněny postačující podmínky pro to, aby účelová funkce f(x) měla v bodě x* ostré lokální maximum (účelová funkce f(x) je v okolí bodu x* ryze konkávní).
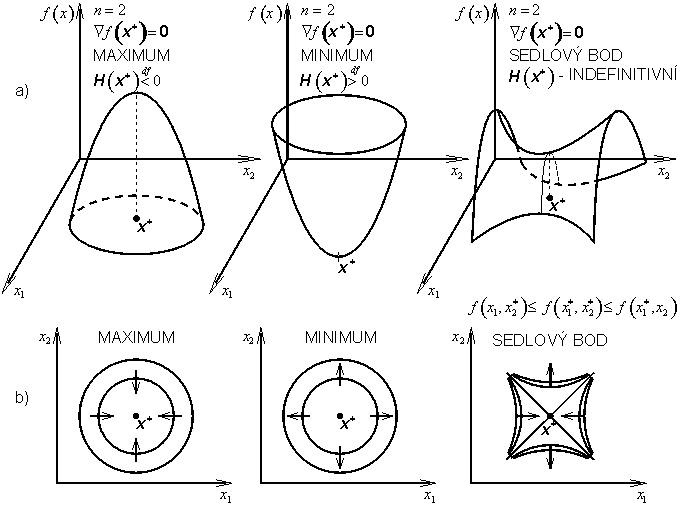
Nemá-li účelová funkce f(x) ve stacionárním bodě extrém a je-li Hessova matice H(x*) indefinitní, pak stacionární bod x* je lokálním sedlovým bodem.
|
|
Uvedené tři základní případy jsou ukázány na obr. 3.1. K zobrazení účelové funkce f(x) na obr. 3.1b jsou použity hladiny (vrstevnice, izolinie), tj. množiny konstantních hodnot účelové funkce f(x). Tyto množiny jsou obecně dány vztahem
|
(3.19) |
Šipky ukazují směr růstu hodnot účelové funkce f(x). Směr největšího růstu (stoupání) v některém bodě vyjadřuje gradient (3.6) účelové funkce f(x), který je vždy kolmý na hladinu procházející daným bodem.
Je třeba analyticky řešit optimalizační úlohu
pro:
a) 
b) 
c) 
d) 
e) 
Řešení:
a)
H1 = 2 > 0, H2 = 4 > 0 => 
=> Ostré lokální minimum
f * = f(x *) = 0
Hessova matice je kladně definitní jak ve stacionárním bodě x*, tak i v libovolném jiném bodě 
, a proto účelová funkce f(x) je ryze konvexní a má v bodě x* = [0, 0]T ostré globální minimum.
|
|
b)
H1 = -2 < 0, H2 = -4 < 0 => H(x*) – indefinitní => sedlový bod
Hessova matice H(x*) je indefinitní, a proto stacionární bod x* = [0, 0]T je sedlovým bodem a účelová funkce f(x) v tomto bodě extrém nemá.
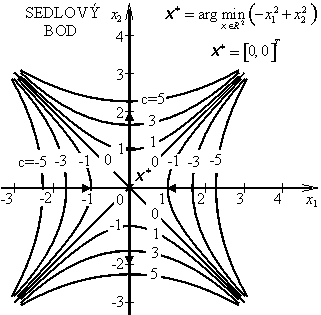 Příklad 3.1b |
c)
H1 = 2 > 0, H2 = 0 => 
Hessova matice H(x*) je kladně semidefinitní, ale ve stacionárním bodě x* = [0, 0]T extrém nevystupuje, protože účelová funkce f(x) v okolí bodu x* není konvexní, ani konkávní (Hessova matice v okolí stacionárního bodu mění svou definitnost).
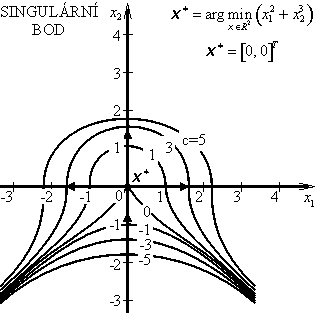 Příklad 3.1c |
d)
H1 = 2 > 0, H2 = 0 =>
Hessova matice H(x) je ve stacionárním bodě x* kladně semidefinitní a proto pro libovolné jiné body – kladně definitní, a proto účelová funkce f(x) je ryze konvexní a má v bodě x* = [0, 0]T ostré globální minimum: f * = f(x*) = 0.
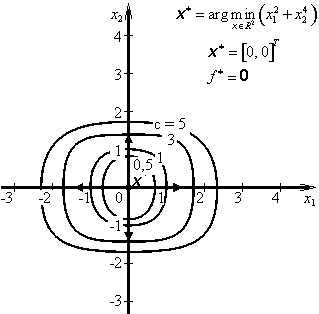 Příklad 3.1d |
e)
– celá souřadnicová osa x2 tvoří množinu stacionárních bodů
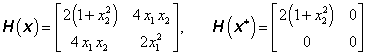
Hessova matice H(x) je ve stacionárních bodech x* = [0, x2]T kladně semidefinitní a účelová funkce f(x) má v těchto bodech neostré globální minimum: f *= f(x*) = 0.
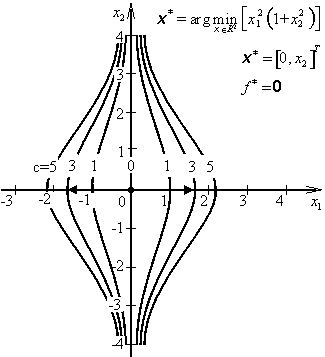 Příklad 3.1e |