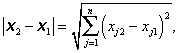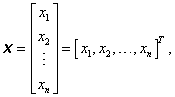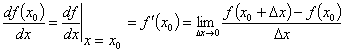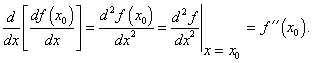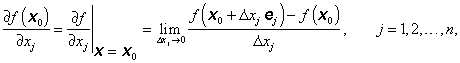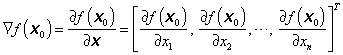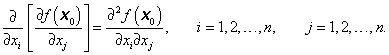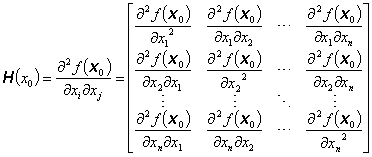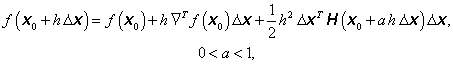1 Úvod do optimalizace

1.2 Základní pojmy z teorie optimalizace

1.2.1 Prostor, bod, funkce, množina

Eukleidovský n-rozměrný prostor Rⁿ je množinou všech uspořádaných n-tic reálných čísel ,zvaných body nebo vektory, s eukleidovskou vzdáleností (metrikou)

(1.1)

kde , resp. jsou souřadnice bodu x₁, resp. x₂.

Body ztotožňujeme tedy s vektory (obr. 1.1), které budeme zapisovat jako sloupcové, tj.

(1.2)

kde T je symbol transpozice.

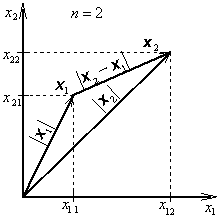Obr. 1.1: Vektor

Jsou-li x₁a x₂ dva nenulové vektory a φ je úhel, který svírají, pak jejich skalární součin je definován vztahem

(1.3)

Poznámka: Protože všechny vlastnosti, které platí v dvojrozměrném prostoru R² , tj. euklidovské rovině, platí i v libovolném konečněrozměrném prostoru Rⁿ proto pro názornou geometrickou interpretaci budeme používat R² a R³.

Množinu

(1.4)

nazýváme okolím bodu x₁ (obr. 1.2).

Obr. 1.2: Okolí bodu

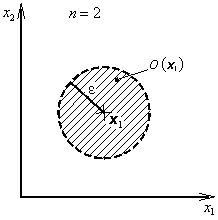
Bod x je vnitřním bodem množiny , existuje-li takové okolí bodu x, že platí (obr. 1.3)

(1.5)

Obr. 1.3: Vnitřní body množiny

Bod x je hraničním bodem množiny , obsahuje-li libovolné okolí bodu x alespoň jeden bod z X a alespoň jeden bod nepatřící do X (obr. 1.4)

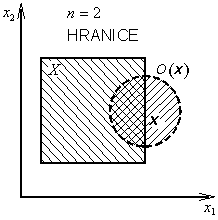Obr. 1.4: Hraniční okolí bodu

Množina všech hraničních bodů množiny X tvoří hranici množiny X (obr. 1.4)

Hraniční bod množiny X nemusí přirozeně do množiny X patřit.

Hraniční bod x množiny X, je krajním bodem množiny X, když pro libovolné dva navzájem různé body x₁ a x₁ z X tento bod nemůže být vyjádřen vztahem (viz např. body na obr. 1.9):

(1.6)

Množinase nazývá otevřená, má-li pouze vnitřní body (obr.1.3).

Otevřenou množinou je tedy i okolí, viz obr. 1.2.

Množinase nazývá uzavřená, obsahuje-li všechny své hraniční body (obr 1.4).

Množina se nazývá ohraničená (omezená), je-li euklidovská vzdálenost mezi dvěma libovolnými body z X konečná (konečné číslo). Jinak množina je neohraničená (neomezená), viz obr. 1.5.

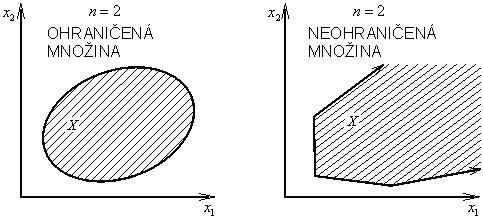Obr. 1.5: Ohraničená a neohraničená množina

Uzavřená a ohraničená množina se nazývá kompaktní (obr. 1.6).

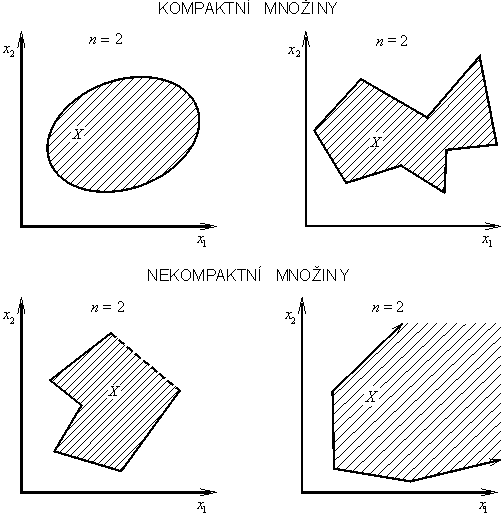Obr. 1.6: Kompaktní a nekompaktní množiny

Množina se nazývá konvexní, platí-li pro dva libovolné navzájem různé body x₁ a x₂ z X

(1.7)

Tzn. konvexní množina obsahuje spolu se svými dvěma libovolnými body i úsečku, která tyto body spojuje (obr. 1.7)

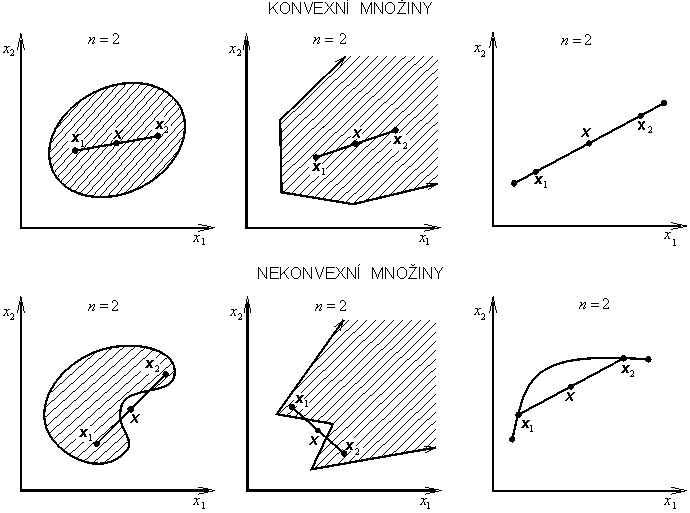Obr. 1.7: Konvexní a nekonvexní množiny

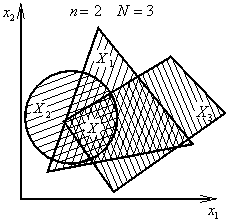
Jsou-li množiny konvexní, pak množina

(1.8)

je také konvexní (obr. 1.8). Tzn. průnik konečného počtu konvexních množin je konvexní množinou.

Obr. 1.8: Konvexní množiny

Množina určená vztahem

(1.9)

je konvexní (obr. 1.9).

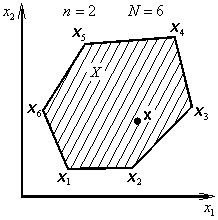Obr. 1.9: Konvexní množina

Tzn. konvexní kombinace bodů vytvoří konvexní množinu.

Reálná funkce f(x) se nazývá konvexní na množině , když pro libovolné dva navzájem různé body x₁ a x₂ z X platí

(1.10)

Platí-li nerovnost (1.10) jako ostrá, pak funkce f(x) je na množině X ryze konvexní (obr. 1.10).

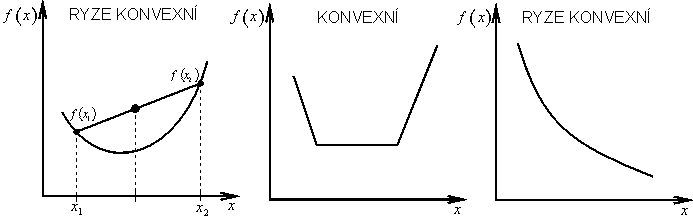Obr. 1.10: Ryze konvexní a konvexní množina

Jsou-li funkce konvexní na konvexní množině , pak funkce

(1.11)

je také konvexní na množině X. Tzn. lineární kombinace s nezápornými váhovými koeficienty konvexních funkcí tvoří rovněž konvexní funkci (obr. 1.11).

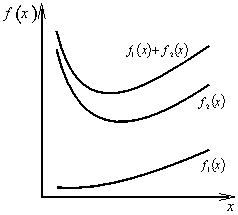Obr. 1.11: Lineární kombinace konvexních funkcí

Funkce f(x) je konkávní, resp. ryze konkávní, když funkce -f(x) je konvexní, resp. ryze konvexní (obr. 1.12 a obr. 1.13).

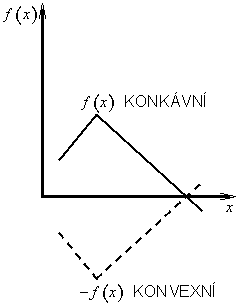Obr. 1.12: Konkávní funkce

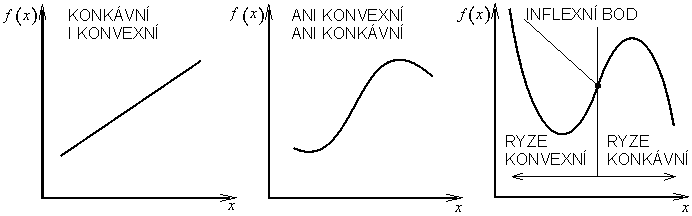Obr. 1.13: Konvexnost a konkávnost funkce

Bude-li funkce g(x) konvexní, resp. konkávní, pak množina určená vztahem

(1.12)

resp.

(1.13)

bude také konvexní (obr. 1.14a, resp. obr. 1.14b).

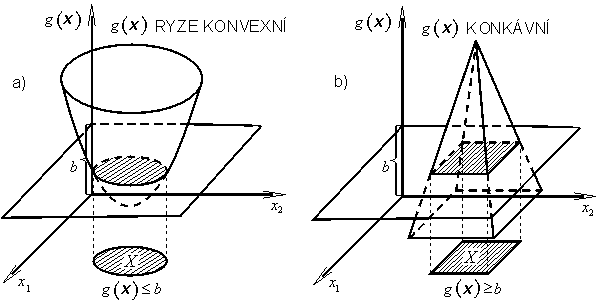Obr. 1.14: Ryze konvexní a konkávní funkce

1.2.2 Derivace funkce

Derivace (první, prvního řádu) funkce jedné proměnné f(x) v bodě x₀ je definována vztahem

(1.14)

za předpokladu, že tato limita existuje (obr. 1.15).

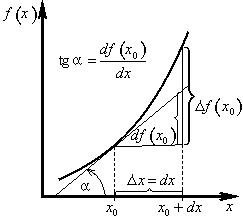Obr. 1.15: Přírůstek funkce

Funkce jedné proměnné f(x), která má spojitou derivaci na intervalu , se nazývá hladká na intervalu .

Ze vztahu (1.14) dostaneme

(1.15)

kde df(x₀) je diferenciál funkce f(x) v bodě x₀ (přírůstek na tečně), dx je diferenciál nezávislé proměnné x.

Diferenciál pro aproximuje v bodě x₀ přírůstek funkce [obr. 1.15, viz též vztah (1.29)]

(1.16)

Má-li funkce jedné proměnné f(x) na intervalu diferenciál, pak se nazývá diferencovatelná na intervalu . U funkcí jedné proměnné tedy existence derivace je ekvivalentní diferencovatelnosti.

Neexistuje-li v bodě x₀ limita (1.14), ale existuje limita zleva , resp. limita zprava , pak funkce f(x) má v bodě x₀ derivaci zleva , resp. zprava , viz obr. 1.16.

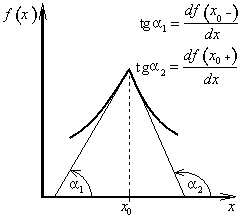Obr. 1.16: Derivace zleva a zprava

Protože derivaci f '(x) lze považovat za funkci proměnné x, proto lze určit v bodě x₀ derivaci této derivace, tj.

(1.17)

Nazýváme ji derivací druhého řádu (druhou derivací) funkce f(x) v bodě x₀.

Podobně je možno určit i derivace vyšších řádů.

1.2.3 Parciální derivace funkce a totální diferenciál

Parciální derivace (první, prvního řádu) funkce n-proměnných f(x) v bodě x, podle proměnné x_j je definovaná vztahem (za předpokladu, že tato limita existuje)

(1.18)

kde je n-rozměrný jednotkový vektor s jedničkou na j-té pozici.

Parciální derivaci funkce f(x) podle proměnné x_j, (j = 1, 2, ..., n) určíme obyčejným derivováním funkce f(x) podle proměnné x_j, přičemž všechny ostatní proměnné pokládáme za konstanty (obr. 1.17).

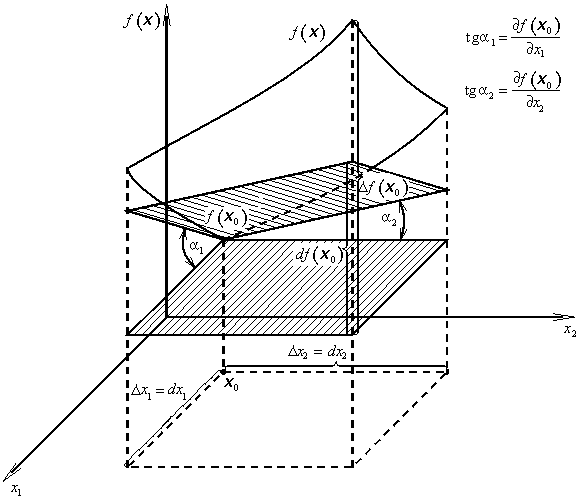Obr. 1.17: Totální diferenciál funkce

Totální (úplný) diferenciál funkce n-proměnných f(x) v bodě x₀ (přírůstek na tečné nadrovině) je dán vztahem (obr. 1.17)

(1.19)

kde 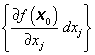jsou parciální diferenciály funkce f(x) v bodě x₀,

jsou diferenciály odpovídajících nezávisle proměnných .

Funkce n-proměnných f(x), která má na nějaké otevřené množině totální diferenciál, se nazývá diferencovatelná na této množině. Protože existence totálního diferenciálu je spojena nejenom s existencí všech parciálních derivací , ale i s požadavkem jejich spojitosti, proto existence parciálních derivací u funkce n-proměnných není ekvivalentní diferencovatelnosti, jak je tomu u funkce jedné proměnné.

Vztah (1.19) lze pomocí skalárního součinu zapsat ve tvaru

(1.20)

kde

(1.21)

je vektor parciálních derivací funkce f(x) v bodě x₀, který se nazývá gradient a

(1.22)

je vektor diferenciálů nezávisle proměnných.

Diferenciál df(x₀) pro aproximuje v bodě x₀ přírůstek funkce [obr. 1.17, viz též vztah (1.30)]

(1.23)

Limitu (pokud existuje)

(1.24)

kde s je jednotkový směrový vektor (tj. |s| = 1), nazýváme derivací funkce f(x) v bodě x₀ ve směru s (obr. 1.18).

Obr. 1.18: Derivace funkce f(x) v bodě x₀ ve směru s

Funkce n-proměnných f(x), která je diferencovatelná v bodě x₀, má v tomto bodě i derivaci v libovolném směru s a platí

(1.25)

Označíme-li si písmenem φ úhel, který svírá gradient se směrem s, pak vztah (1.25) shodně s (1.3) lze zapsat ve tvaru

(1.26)

z něhož vyplývá, že funkce f(x) má v bodě x₀ největší derivaci ve směru určeném gradientem , protože v tomto směru má cos φ největší hodnotu (tj. cos φ = 1), tzn. gradient určuje směr největšího růstu funkce f(x) v bodě x₀.

Budou-li parciální derivace v bodě x₀ diferencovatelné, pak je možno derivovat je ještě jednou a dostaneme parciální derivace druhého řádu (druhá parciální derivace)

(1.27)

Pro se tyto parciální derivace nazývají smíšené. Budou-li smíšené parciální derivace druhého řádu spojité, pak nezáleží na pořadí derivování, tj. nezáleží na pořadí proměnných, podle kterých derivujeme.

Čtvercová matice otevřená s n² parciálních derivací druhého řádu funkce f(x) v bodě x₀, tj.

(1.28)

se nazývá Hessova matice (hessián).

Má-li funkce jedné proměnné f(x) spojitou derivaci druhého řádu, pak ji lze v okolí bodu x₀ rozložit podle Taylorova vzorce se zbytkem v Lagrangeově tvaru, tj.

(1.29)

kde je zbytek v Lagrangeově tvaru.

Podobně, je-li funkce n-proměnných f(x) dvakrát spojitě diferencovatelná, pak ji lze v okolí bodu h = 0, a tedy i x₀ rovněž rozložit podle Taylorova vzorce se zbytkem v Lagrangeově tvaru, tj.

(1.30)

kde je zbytek v Lagrangeově tvaru, (speciálně může být h = 1).

1.2.4 Extrémy funkce

Funkce f(x) definovaná na množině má v tomto bodě lokální (relativní) minimum, platí-li pro všechny body nerovnost

(1.31)

Je-li nerovnost (1.31) splněna pro body jako ostrá, tj.

(1.32)

pak funkce f(x) má v bodě ostré (silné) lokální minimum.

Platí-li neostrá nerovnost (1.31), resp. ostrá nerovnost (1.32) pro všechny body pak funkce f(x) má v bodě x^* globální (absolutní), resp. ostré globální minimum. Ostré globální minimum je vždy jednoznačné. Je zřejmé, že každé globální minimum je zároveň lokálním minimem.

Zaměníme-li ve vztazích (1.31) a (1.32) znaky nerovností na opačné, dostaneme vztahy definující odpovídající druh maxima (obr. 1.19).

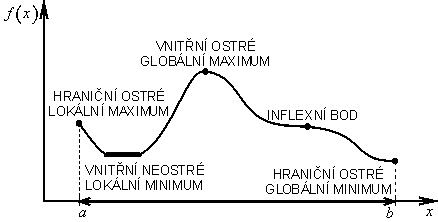Obr. 1.19: Extrémy funkce

Společný název pro minimum a maximum je extrém. Body , ve kterých funkce f(x) má extrém, tj. funkce f(x) nabývá extremální (minimální, nebo maximální) hodnoty, se nazývají extremální body funkce f(x) na množině X.

Funkce f(x), která má na množině X pouze jeden extrém (daného druhu), se nazývá unimodální. V opačném případě je multimodální.

Je-li extremální bod vnitřním bodem množiny X, tj. existuje takové okolí bodu x^*, že platí

(1.33)

pak funkce f(x) má v bodě x^* vnitřní (volný, nepodmíněný) extrém. V opačném případě, tj. když extremální bod x^* je hraničním bodem množiny X, funkce f(x) má v bodě x^* hraniční (vázaný, podmíněný) extrém.

1.2.5 Druhy podmínek

Při určování extrémů funkce f(x) budeme používat tři druhy podmínek:

a) Nutné podmínky (NP) existence extrému (E)

Má-li funkce f(x) v bodě extrém, pak v tomto bodě musí být splněny nutné podmínky existence extrému. Nebudou-li v bodě splněny nutné podmínky existence extrému, pak v tomto bodě funkce f(x) nemá extrém. Tento kauzální vztah lze symbolicky vyjádřit zápisem

(1.34)

resp.

(1.35)

b) Postačující podmínky (PP) existence extrému (E)

Budou-li v bodě splněny postačující podmínky existence extrému, pak funkce f(x) bude mít v tomto bodě extrém. Naproti tomu nemá-li funkce f(x) v bodě extrém, pak postačující podmínky existence extrému nemusí být splněny. Symbolicky tento kauzální vztah lze zapsat ve tvaru

(1.36)

resp.

(1.37)

c) Nutné a postačující podmínky (NPP) existence extrému (E)

Budou-li v bodě splněny nutné a postačující podmínky existence extrému, pak funkce f(x) má v tomto bodě extrém. Lze rovněž říct – má-li funkce f(x) v bodě extrém, pak musí být rovněž splněny nutné a postačující podmínky existence extrému. Kauzální vztah zde platí v obou směrech, tj.

(1.38)

resp.

(1.39)

V uvedených podmínkách značí:

– negace,

– implikace,

– ekvivalence

1.2.6 Minimalizace funkce

Množinu X budeme nazývat množinou přípustných řešení (bodů, vektorů) a funkci f(x) – účelovou funkcí nebo kritériem optimality.

Nyní si můžeme formulovat obecný problém statické optimalizace ve tvaru úlohy minimalizace účelové funkce f(x) na množině přípustných řešení

(1.40)

resp.

(1.41)

kde

(1.42)

Úlohu maximalizace účelové funkce f(x) na množině přípustných řešení X lze rovněž zastoupit úlohou minimalizace (1.40), resp. (1.41), protože platí (obr. 1.20, viz také obr. 1.12)

(1.43)

resp.

(1.44)

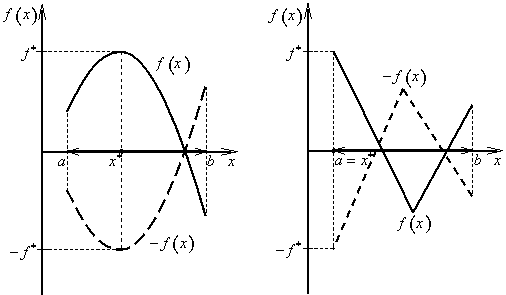Obr. 1.20: Úlohy minimalizace a maximalizace

Platí dokonce obecnější vztahy

(1.45)

resp.

(1.46)

kde a je libovolné číslo, b je libovolné kladné číslo.

Proto se dále budeme zabývat především minimalizací.

V úloze minimalizace (1.40), resp. (1.41) je třeba určit vždy globální minimum účelové funkce f(x) na množině přípustných řešení X. Protože všechny doposud známé metody řešení těchto úloh dovolují určit pouze lokální minima (extrémy), k vyznačení globálního minima je třeba disponovat dodatečnou informací o vlastnostech účelové funkce f(x) a množiny přípustných řešení X.

1.2.7 Věty o extrémech

Pro statickou optimalizaci má základní význam Weierstrassova věta:

„Nechť neprázdná množina přípustných řešení X je kompaktní [tj. omezená (ohraničená) a uzavřená], pak spojitá účelová funkce f(x) definovaná na této množině nabývá na ní globálního minima i maxima“.

Předpoklady o vlastnostech účelové funkce f(x) mohou být oslabeny a nahrazeny podmínkou:

a) globální minimum – účelová funkce f(x) musí být zdola omezená na množině X;

b) globální maximum – účelová funkce f(x) musí být shora omezená na množině X .

Podmínky Weierstrassovy věty jsou postačující.

Další důležitou větou statické optimalizace je věta vyjadřující postačující podmínky pro globální extrémy:

„Nechť neprázdná množina přípustných řešení X je kompaktní a konvexní, účelová funkce f(x) je spojitá a konvexní (resp. konkávní) na X, pak platí:

a) lokální minimum (resp. maximum) je globálním minimem (resp. maximem);

b) množina bodů, na které účelová funkce f(x)dosahuje minima (resp. maxima) je konvexní;

c) pro ryze konvexní (resp. konkávní) účelovou funkci f(x) lokální minimum (resp. maximum) je jednoznačným ostrým globálním minimem (resp. maximem)“.

Dosud jsme uvažovali kritérium optimality ve tvaru účelové funkce, tj. reálné funkce reálných proměnných. V tomto případě optimalizace se nazývá statická a spočívá v minimalizaci (maximalizaci) funkce. Pro statickou optimalizaci se rovněž používá ekvivalentní pojem matematické programování.

V některých případech kritérium optimality může mít tvar účelového funkcionálu, tj. reálného funkcionálu, u kterého nezávisle proměnné jsou reálné funkce reálné proměnné (nejčastěji času). Řešením těchto problémů se zabývá dynamická optimalizace a spočívá v minimalizaci (maximalizaci) daného funkcionálu.