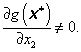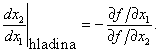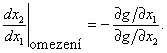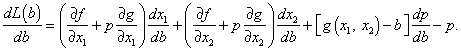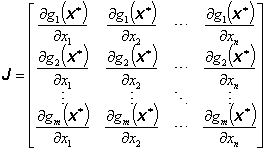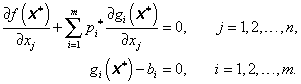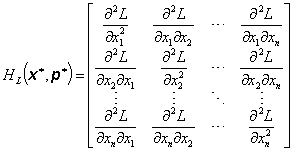3 Statická optimalizace funkcí více proměnných

3.2 Omezeními ve tvaru rovností

Optimalizační úlohy s omezeními ve tvaru rovností (klasické úlohy na vázaný extrém) lze vyjádřit ve tvaru

(3.20)

kde g(x) = [g₁(x), g₂(x), …, g_m(x)]^T – vektor omezujících (vazebních) funkcí,

b = [b₁, b₂, …, b_m]^T – vektor omezujících (vazebních) konstant.

Rozdíl

(3.21)

se nazývá stupeň volnosti úlohy. Pro s = 0 optimalizační úloha (3.20) spočívá v nalezení řešení soustavy n = m obecně nelineárních rovnic

(3.22)

Z těchto řešení se pak srovnáním funkčních hodnot vyčlení optimální řešení x^*, pro které účelová funkce f(x) nabývá globálního minima na množině přípustných řešení X.

Značně důležitější je případ s > 0, tj. n > m. Pro řešení takových optimalizačních úloh se nejčastěji používá Lagrangeova metoda mající v teorii optimalizace základní význam.

Uvažujme úlohu minimalizace

(3.23)

tj. s = 1, n = 2 a m = 1.

Předpokládejme, že v bodě existuje lokální řešení optimalizační úlohy (3.23) a že v tomto bodě jedna z parciálních derivací prvního řádu omezující funkce je nenulová. Např. proměnné x₁ a x₂ jsou očíslovány tak, že platí

(3.24)

Pak vztah pro totální (úplný) diferenciál

(3.25)

lze v okolí bodu x^* zapsat ve tvaru

(3.26)

Řešením této rovnice je

(3.27)

kde

(3.28)

Nyní již můžeme výchozí úlohu vyjádřit ve tvaru optimalizační úlohy s jednou proměnnou bez omezení

(3.29)

pro kterou nutná podmínka prvního řádu je dána vztahem

(3.30)

Po dosazení vztahu (3.28) do podmínky (3.30) a úpravě dostaneme

(3.31)

Zavedeme novou proměnnou

(3.32)

a po dosazení (3.32) do (3.31) a ze samotného vztahu (3.32) obdržíme nutné podmínky prvního řádu pro existenci lokálního řešení úlohy (3.23), tj.

(3.33)

(3.34)

resp. po vyloučení proměnné

(3.35)

Totální diferenciál účelové funkce f(x) při posuvu podél, hladiny [f(x) = konst.] je dán vztahem

(3.36)

Z posledního vztahu vyplývá vlastnost směrnice tečny ke hladině

(3.37)

Vztah (3.26) vyjadřuje směrnici tečny ke křivce omezení

(3.38)

Ze srovnání vztahů (3.35), (3.37) a (3.38) plyne, že lokální řešení x^* úlohy (3.23) vystupuje v bodě dotyku křivek hladiny a omezení, tj. v bodě, ve kterém obě křivky mají společnou tečnu (obr. 3.2).

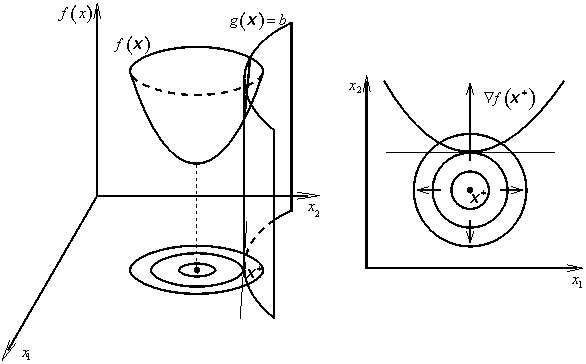Obr. 3.2: Úlohy s omezeními ve tvaru rovnosti

Nutné podmínky prvního řádu (3.33), (3.34) a výchozí omezení lze získat z podmínek stacionarity funkce

(3.39)

tj.

(3.40)

resp. po rozepsání

(3.41)

(3.42)

(3.43)

Proměnná p se nazývá Lagrangeův multiplikátor (Lagrangeův neurčitý koeficient). Pro tuto proměnnou se rovněž používají jiné symboly: λ, u, φ, μ, atd. Funkce (3.39) je tzv. Lagrangeova funkce.

Je-li splněna podmínka (3.24), pak existuje jediný Lagrangeův multiplikátor p^* odpovídající možnému lokálnímu řešení .

Nyní si ukážeme, jakou interpretaci má Lagrangeův multiplikátor p^*. Uvažujme Lagrangeovu funkci L jako funkci omezující konstanty b:

(3.44)

Derivováním podle b dostaneme

Pro optimální proměnné , a p^* platí

(3.45)

a protože

(3.46)

dostaneme velmi důležitý vztah

(3.47)

Vidíme, že optimální hodnota Lagrangeova multiplikátoru p^* vyjadřuje citlivost (senzitivitu) optimální hodnoty účelové funkce f ^* na změnu hodnoty omezující konstanty b.

Podobně lze postupovat i při řešení obecné optimalizační úlohy s omezeními ve tvaru rovností (3.20) pro m < n > 2. Využívá se zde věty o implicitních funkcích, která vyjadřuje Jacobiovy podmínky (jsou to postačující podmínky) pro to, aby v okolí bodu x^* bylo možné vyřešit soustavu rovnic

(3.48)

vzhledem některým m proměnných, např. x₂ = [x₁, x₂, …, x_m]^T vyjádřených ve funkci zbývajících n - m proměnných x₁ = [x_m+₁, x_m+₂, …, x_n]^T tj. [viz vztah (3.27)]

(3.49)

resp.

(3.50)

Tyto podmínky spočívají v tom, že vektorová funkce g(x) má spojité všechny parciální derivace prvního řádu (je spojitě diferencovatelná) a hodnost Jacobiovy matice

(3.51)

je rovna počtu řádků m.

Pak optimalizační úlohu s omezeními ve tvaru rovností (3.20) lze zastoupit (n - m) = s – rozměrnou optimalizační úlohou bez omezení

(3.52)

Další postup je formálně shodný s výše uvedeným případem pro n = 2 a m = 1. Zavedeme m-rozměrný vektor Lagrangeových multiplikátorů

(3.53)

a utvoříme Lagrangeovu funkci

(3.54)

Nutné podmínky prvního řádu pro existenci lokálního řešení x^* úlohy (3.20) jsou shodné s podmínkami stacionarity Lagrangeovy funkce (3.54), a proto lze psát

(3.55)

Po rozepsání dostaneme

(3.56)

resp.

(3.57)

Z těchto podmínek [viz např. (3.56)] vyplývá, že záporný gradient (antigradient) účelové funkce je dán lineární kombinací gradientů omezujících funkcí . Váhovými koeficienty jsou Lagrangeovy multiplikátory

Řešením soustavy n+m rovnic (3.57) [(3.55) nebo (3.56)] dostaneme n+m neznámých: n proměnných a m Lagrangeových multiplikátorů .

Nutné podmínky druhého řádu spočívají v tom, že Hessova matice

(3.58)

sestavena z parciálních derivací druhého řádu Lagrangeovy funkce L podle proměnných {x_j} musí být kladně (záporně) semidefinitní v bodě lokálního minima (maxima) [x^*, p^*]^T při současném splnění podmínky

(3.59)

kde J je Jacobiova matice (3.51).

Bude-li při splnění podmínky (3.59) Hessova matice Lagrangeovy funkce (3.58) kladně (záporně) definitní, pak nutné podmínky prvního řádu (3.55) [(3.56) nebo (3.57)] jsou zároveň postačujícími podmínkami pro to, aby v bodě x^* účelová funkce f(x) měla ostré lokální minimum (maximum). Samozřejmě se předpokládá, že všechny funkce f(x) a
{g_i(x)}mají v okolí bodu spojité parciální derivace druhého řádu.

Podmínky (3.55) [(3.56) nebo (3.57)] jsou nutné a postačující pro existenci globálního minima (maxima) v případě, že účelová funkce f(x) je konvexní (konkávní) a omezující funkce {g_i(x)} jsou lineární.

V optimálním bodě [x ^*, p ^*]^T platí

(3.60)

(3.61)

resp.

(3.62)

Uvažujme nyní okolí bodu [x^*, p^*] v (n+m)-rozměrném euklidovském prostoru R^n+m. Má-li funkce L(x, p) v bodě x ^* lokální minimum, pak platí [viz vztah (3.60)]

(3.63)

Protože , pro libovolný vektor p platí rovnost

(3.64)

a vztah (3.63) lze tedy zapsat ve tvaru

(3.65)

ze kterého vyplývá, že Lagrangeova funkce L(x,p) má v bodě [x^*, p^*]^T lokální singulární sedlový bod [protože na pravé straně vztahu (3.65) je znak rovnosti].

Lagrangeova metoda je velmi výhodná, protože umožňuje převést optimalizační úlohu s omezeními ve tvaru rovností na optimalizační úlohu bez omezení, tzn. dovoluje zastoupit získání lokálních vázaných extrémů účelové funkce f(x) určením lokálních volných extrémů Lagrangeovy funkce L(x, p).

Při řešení konkrétní optimalizační úlohy nejdříve najdeme stacionární body Lagrangeovy funkce L(x,p), potom každý stacionární bod identifikujeme a vzájemným srovnáním funkčních hodnot vyčleníme globální řešení (pokud existuje).

Příklad 3.2

Lagrangeovou metodou vyřešte úlohu minimalizace

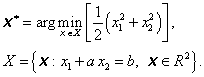
Řešení:

Jacobiova matice J = [1, a] má hodnost 1.

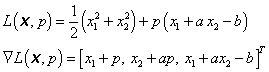
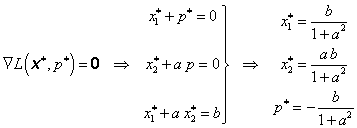
Hessova matice

je kladně definitní, a proto účelová funkce f(x) je ryze konvexní. Omezující funkce g(x) je lineární, proto účelová funkce f(x) nabývá v bodě ostrého globálního minima.

Optimální hodnota účelové funkce f(x^*) = f ^* je dána vztahem

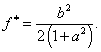
Po derivování podle omezující konstanty b, dostaneme

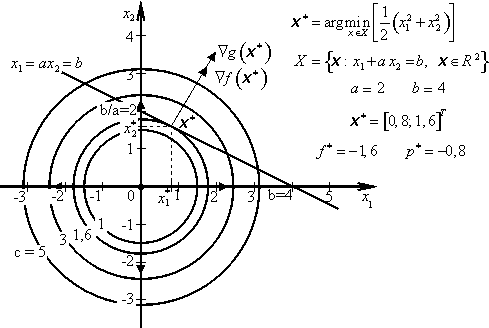Příklad 3.2