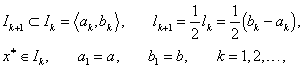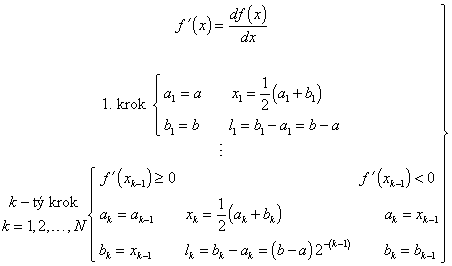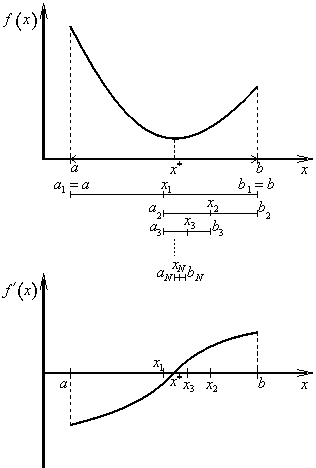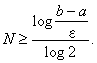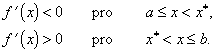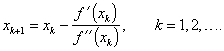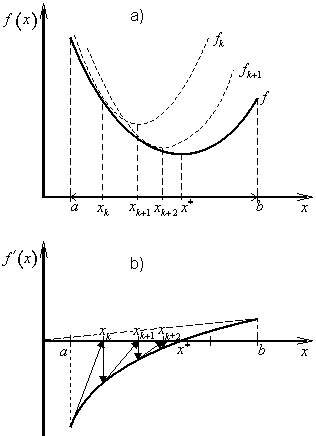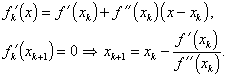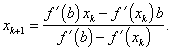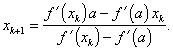2 Statická optimalizace funkcí jedné proměnné

2.2 Numerické metody jednorozměrné optimalizace

Numerické metody jednorozměrné optimalizace lze rozdělit na dvě základní skupiny:

diferenciální (gradientní) metody – vyžadují určování hodnot účelové funkce a její první, resp. druhé derivace
přímé metody – vyžadují pouze určování hodnot účelové funkce.

Budeme se zde zabývat numerickými metodami jednorozměrné minimalizace spojitých unimodálních funkcí (jsou to takové funkce, které mají jeden extrém na daném intervalu), tj. řešením optimalizační úlohy

(2.5)

(2.6)

Není-li daná účelová funkce f(x) na intervalu unimodální, pak je třeba přibližně určit polohu bodu globálního minima a interval zmenšit tak, aby na zmenšeném intervalu účelová funkce f(x) byla unimodální.

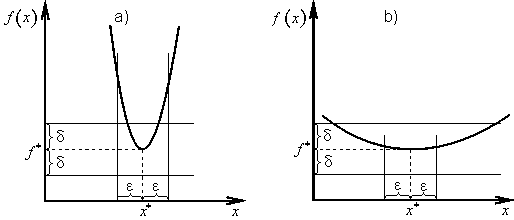
U numerických metod je nutno předem zadat požadovanou přesnost vyznačení optimálního řešení x^*, tj. nezáporné číslo ε, pro které N-tá aproximace řešení x_N musí vyhovovat nerovnosti

(2.7)

a také požadovanou přesnost vyznačení optimální hodnoty účelové funkce f ^*, tj. nezáporné číslo δ, pro které hodnota účelové funkce v bodě x_N vyhovuje nerovnosti (obr. 2.4)

(2.8)

Obr. 2.4: Přesnost řešení

U některých numerických metod kontrola splnění podmínek (2.7), resp. (2.8) je problematická. Jde především o ty případy, kdy informace o vlastnostech účelové funkce f(x) jsou velmi nedostatečné, proto se rovněž používají vztahy

(2.9)

resp.

(2.10)

2.2.1 Diferenciální metody

Budeme uvažovat hladkou unimodální účelovou funkci f(x) na intervalu mající ostré globální minimum v jediném stacionárním bodě, který je reálným kořenem rovnice

(2.11)

V jednodušších případech lze rovnici (2.11) řešit analyticky. Bude-li tato rovnice transcendentní (nealgebraická), její řešení musíme hledat pomocí numerických iteračních metod.

a) Bolzanova metoda

Nejjednodušší iterační metodou jednorozměrné minimalizace je Bolzanova metoda (metoda půlení intervalu, metoda dichotomie), kterou využijeme pro řešení rovnice (2.11). Bolzanova metoda spočívá v utvoření takové posloupnosti intervalů

(2.12)

pro kterou platí vztahy

(2.13)

kde l_k je délka intervalu I_k.

Ze vztahů (2.13) v limitě dostaneme

(2.14)

(2.15)

Interval I_k nazýváme k-tým intervalem neurčitosti nebo lokalizace.

Bolzanova metoda může být popsána následujícím algoritmem (obr. 2.5):

(2.16)

Obr. 2.5: Princip Bolzanovy metody

Po N-tém kroku optimální bod x^* leží v intervalu neurčitosti I_N a proto lze psát

(2.17)

kde

(2.18)

Nutný počet kroků N při lokalizace optimálního bodu x^* s přesností dostaneme úpravou vztahů (2.17) a (2.18)

(2.19)

V algoritmu (2.16) se využívá vlastnosti hladké unimodální účelové funkce f(x), která může být vyjádřena nerovnostmi

(2.20)

Bolzanova metoda je vždy konvergentní, pokud jsou splněny její podmínky (2.20), ale rychlost konvergence je malá.

Příklad 2.4

Bolzanovou metodou vyřešte optimalizační úlohu z příkladu 2.1 s přesností ε = 0,01

Řešení:

Potřebný počet kroků vypočteme ze vztahu

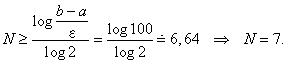
Shodně s algoritmem Bolzanovy metody (2.16) lze psát:

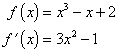
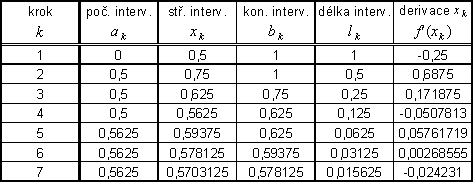
Jednotlivé kroky řešení:

1. krok:	a₁ = a = 0	b₁ = b = 1	x₁ = 0,5	f '(x₁) = -0,25 < 0
2. krok:	a₂ = x₁ = 0,5	b₂ = b₁ = 1	x₂ = 0,75	f '(x₂) = 0,6875 > 0
3. krok:	a₃ = a₂ = 0,5	b₃ = x₂ = 0,75	x₃ = 0,625	f '(x₃) = 0,17188 > 0
4. krok:	a₄ = a₃ = 0,5	b₄ = x₃ = 0,625	x₄ = 0,5625	f '(x₄) = -0,05078 < 0
5. krok:	a₅ = x₄ = 0,5625	b₅ = b₄ = 0,625	x₅ = 0,59375	f '(x₅) = 0,05762 > 0
6. krok:	a₆ = a₅ = 0,5625	b₆ = x₅ = 0,59375	x₆ = 0,57813	f '(x₆) = 0,00269 > 0
7. krok:	a₇ = a₆ = 0,5625	b₇ = x₆ = 0,57813	x₇ = 0,57031

Výsledek zapíšeme:

l₇ = b₇ - a₇ = 0,01563

Přibližné řešení:

Přesné řešení:

Výsledek řešení ze souboru v Excelu (StatOpt-BolzMet.xls):

b) Newtonova metoda

Mezi základní iterační metody řešení rovnice (2.11) patří Newtonova metoda (Newtonova-Raphsonova metoda, metoda tečen). Tato metoda spočívá v utvoření posloupnosti bodů podle Newtona rekurentního vzorce

(2.21)

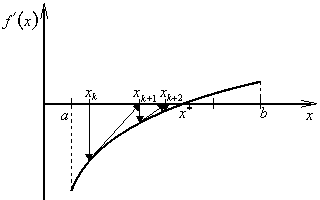
Metoda odpovídá sestrojení tečny v bodě funkce f '(x), viz obr. 2.6. Průsečík tečny s osou X, tj. bod x_k+1 je (k+1)-ní aproximace kořene rovnice (2.11), a tedy i optimálního bodu x^*.

Obr. 2.6: Princip Newtonovy metody

Postačujícími podmínkami konvergence posloupnosti bodů k optimálnímu bodu x^*, tj.

(2.22)

jsou:

(2.23)

(2.24)

(2.25)

Za počáteční aproximaci je vhodné volit takový bod x₁, který vyhovuje nerovnosti

(2.26)

Při nevhodné volbě počátečního bodu x₁ další aproximace může ležet vně intervalu , viz obr. 2.6b.

Newtonův rekurentní vzorec (2.21) má ještě jednu velmi názornou interpretaci. V okolí bodu x_k účelovou funkci f(x) zastoupíme prvními třemi členy Taylorova rozvoje (kvadratickou parabolou)

(2.27)

Za (k+1)-ní aproximaci optimálního bodu X zvolíme bod x_k+1, ve kterém funkce f_k(x) nabývá svého ostrého globálního minima. Z nutné podmínky dostaneme (obr. 2.6a)

(2.28)

Obdrželi jsme Newtonův rekurentní vzorec (2.21).

Odhad přesnosti N-té aproximace lze provést např. podle vztahu

(2.29)

kde

(2.30)

Konvergence Newtonovy metody je tím rychlejší, čím více se účelová funkce f(x) blíží kvadratické parabole, pro kterou přesné řešení dostaneme po jednom kroku.

Newtonova metoda má některé velmi nepříjemné vady. Nejdůležitější jsou:

příliš tvrdé postačující podmínky konvergence (2.23) – (2.25),
v každé iteraci je třeba počítat první f '(x) a druhou derivaci f ''(x).

V praxi je možno použít modifikaci Newtonovy metody spočívající v tom, že když druhá derivace f ''(x) se již mnoho nemění, lze ji ponechat beze změny i pro následující iterace, tj. použijeme vzorce (obr. 2.7)

(2.31)

kde B je konstanta rovná posledně vypočtené druhé derivaci f ''(x) . Tato modifikovaná metoda se někdy také nazývá Whittakerova metoda.

Obr. 2.7: Princip modifikované Newtonovy metody

U Newtonovy metody se nevypočítává počet kroků iterace a výpočet se ukončí když platí a výsledek se zapíše ve tvaru protože se blížíme k extrému účelové funkce f(x) jen z jedné strany.

Příklad 2.5

Optimalizační úlohu z příkladu 2.1 vyřešte Newtonovou metodou a modifikovanou Newtonovou metodou, obě pro přesnost ε_N = 0,001

Řešení:

a) Newtonova metoda

Nejdříve vypočteme všechny požadované derivace účelové funkce:

f '(x) = 3x² - 1

f ''(x) = 6x

f '''(x) = 6

Zkontrolujeme postačující podmínky konvergence:

f '(0) f '(1) = - 2 < 0,

Postačující podmínky konvergence Newtonovy metody jsou splněny pro polouzavřený interval .

Za počáteční aproximaci volíme bod x₁ = 1, protože platí

f '(1) f '''(1) = 12 > 0.

Newtonův rekurentní vzorec má tvar

x₁ = 1
x₂ = 0,66667
x₃ = 0,58333
x₄ = 0,57738
x₅ = 0,57735

|x₅ - x₄| = 0.00003

Přibližné řešení:

b) modifikovaná Newtonova metoda

Ve vzorci (2.31) za B volíme f ''(1) = 6 a dostaneme:

x₁ = 1
x₂ = 0,66667
x₃ = 0,61111
x₄ = 0,59105
x₅ = 0,58305
x₆ = 0,59974
x₇ = 0,57836
x₈ = 0,57778

|x₈ - x₇| = 0.00058

Přibližné řešení:

Přesné řešení:

c) Metoda sečen

Tato metoda vychází z Newtonovy metody a proto pro ni platí stejné postačující podmínky konvergence (2.23) – (2.25).

Zastoupíme-li v Newtonově rekurentním vzorci (2.21) směrnici tečny funkce f '(x) v bodě x_k [tj. výraz f ''(x_k)] směrnicí vhodně volené sečny, např.

(2.32)

(2.33)

pak dostaneme vztah pro metodu sečen

(2.34)

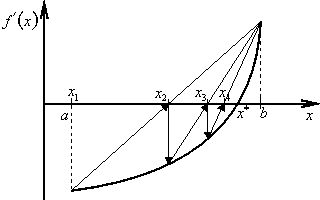
Metoda sečen má několik modifikací. Vztahy (2.32) – (2.34) vyjadřují případ uvedený na obr. 2.8, kdy pevným bodem je bod b a platí pro něj

Obr. 2.8: Princip metody sečen

Pokud to neplatí, bude pevným bodem bod a a vztah (2.34) je třeba upravit na tvar

Vhodnou volbou počátečních aproximací lze u této metody zajistit konvergenci u většiny praktických případů. Rychlost konvergence je pomalejší než u Newtonovy metody. Ukončení iteračního výpočtu a zápis řešení optimalizační úlohy je stejný jako u Newtonovy metody. Výsledek zapisujeme ve tvaru kde pro x_k+1 platí kde ε je zadaná přesnost.

S výhodou se využívá kombinace metody sečen s Newtonovou metodou.

Příklad 2.6

Metodou sečen je třeba řešit optimalizační úlohu z příkladu 2.1 s přesností ε_N = 0,001

Řešení:

Zvolíme si b = 1 a shodně se vztahem (2.34) pro f '(x) = 3x² - 1 dostaneme:

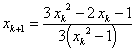
x₁ = 1
x₂ = 0,33333
x₃ = 0,5
x₄ = 0,55556
x₅ = 0,57143
x₆ = 0,57576
x₇ = 0,57692
x₈ = 0,57724

|x₈ - x₇| = 0,00032

Přibližné řešení:

Přesné řešení: