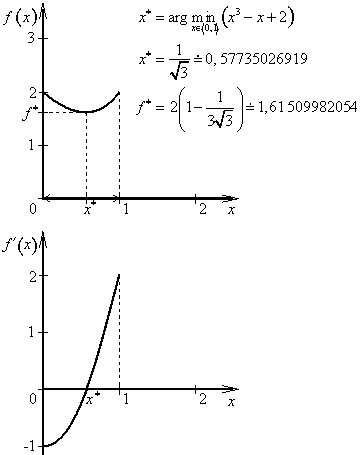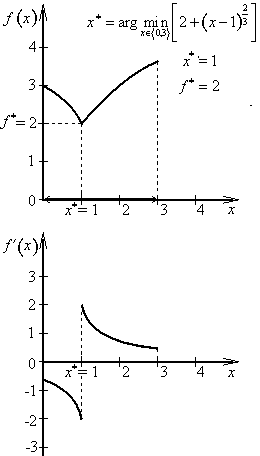2 Statická optimalizace funkcí jedné proměnné

2.1 Analytické metody jednorozměrné optimalizace

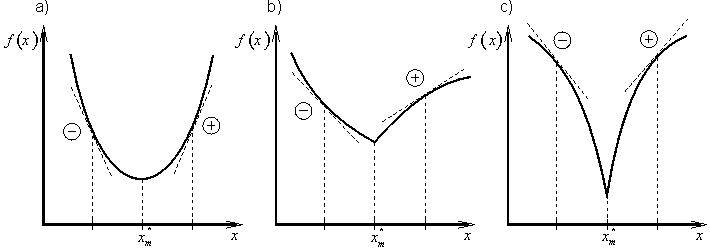
U spojité účelové funkce jedné proměnné f(x) lze nutné podmínky existence lokálního extrému získat analýzou první derivace , viz obr. 2.1. V bodech, ve kterých účelová funkce f(x) má lokální extrém, derivace prvního řádu f '(x) je nulová (obr. 2.1a) nebo neexistuje (obr. 2.1b,c). Na obr. 2.1 a hladká účelová funkce f(x) má v bodech  a  nulovou derivaci f '(x) . Spojitá účelová funkce f(x) na obr. 2.1b má v bodech  a  zlomy, kterým odpovídají body nespojitosti prvního druhu derivace f '(x). V bodech  a  existují pouze derivace zleva a zprava. Případ, kdy derivace f '(x) má body nespojitosti druhého druhu, je na obr. 2.1c.

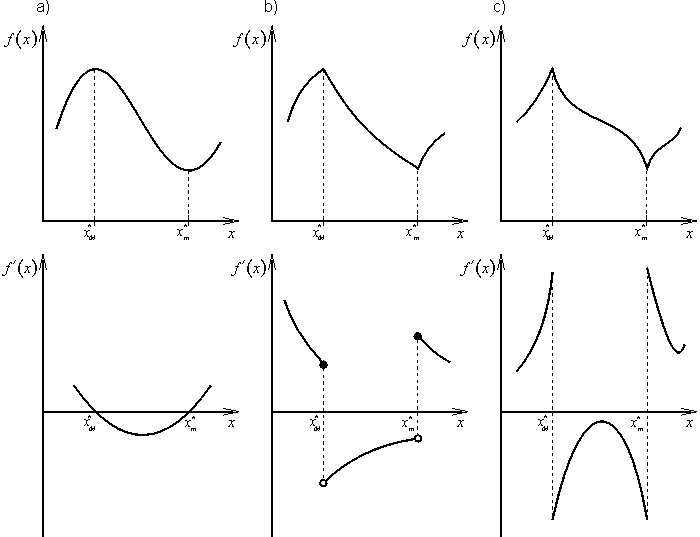Obr. 2.1: Účelová funkce f(x) a její první derivace f '(x)

Nutné podmínky tedy zní:

„Spojitá účelová funkce může mít lokální extrém pouze v těch bodech, ve kterých její první derivace je nulová nebo neexistuje.“

Z obr. 2.2 plyne, že tato podmínka není postačující. Ve všech třech případech nutné podmínky jsou splněny, ale v uvažovaných bodech extrémy nevystupují.

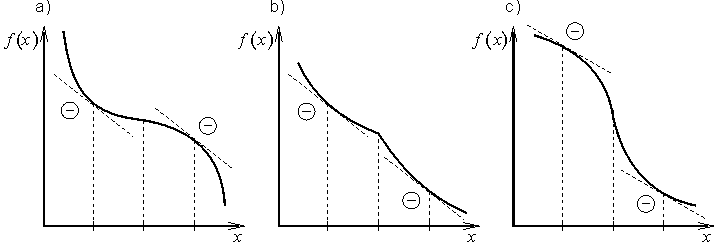Obr. 2.2: Průběhy účelových funkcí, v nichž nevystupují extrémy

Při určování lokálních extrémů spojité účelové funkce f(x) nejdříve na základě nutných podmínek určíme „podezřelé body“ a pak pomocí některé z následujících metod zjistíme průběh účelové funkce v okolí těchto podezřelých bodů.

a) Metoda srovnání hodnot funkce

Tato metoda spočívá ve srovnání hodnot účelové funkce f(x) v podezřelém bodě x^* s hodnotami v bodech  a , které jsou tak blízko bodu x^*, že mezi nimi neleží už žádný jiný podezřelý bod. Platí-li nerovnost

pak shodně s (1.32) v bodě x^* vystupuje ostré lokální minimum. Platí-li opačná nerovnost, pak účelová funkce f(x) má v bodě x^* ostré lokální maximum.

b) Metoda srovnání znamének první derivace

Při této metodě v bodech  a  srovnáváme znaménka první derivace f '(x). Budou-li znaménka první derivace f '(x) v bodech  a  stejná, pak v podezřelém bodě x^* extrém nevystupuje (obr. 2.2). Změní-li se znaménko první derivace f '(x) při přechodu z bodu  do bodu  z (–) na (+), pak účelová funkce f(x) má v bodě x^* ostré lokální minimum (obr. 2.3) a opačně, změní-li se znaménko f '(x) z (+) na (–), ostré lokální maximum.

c) Metoda vyšších derivací

Tuto metodu lze použít pouze v těch případech, kdy v podezřelých bodech existují spojité derivace vyšších řádů. Reálné kořeny rovnice (viz kap.3)

vyznačují podezřelé body, tzv. stacionární (kritické) body, ve kterých vypočteme druhé derivace . Bude-li ve stacionárním bodě druhá derivace f ''(x) kladná, pak účelová funkce f(x) je ryze konvexní a má v tomto bodě ostré lokální minimum a opačně, bude-li záporná, pak účelová funkce f(x) je ryze konkávní a má v tomto bodě ostré lokální maximum. Je-li druhá derivace f ''(x) v nějakém stacionárním bodě nulová a třetí derivace  nenulová, pak účelová funkce f(x) v tomto bodě extrém nemá. Takový stacionární bod se nazývá inflexní. Bude-li i třetí derivace f '''(x) ve stacionárním bodě nulová, je třeba použít následující pravidlo:

„Je-li řád první nenulové derivace ve stacionárním bodě lichý, pak v tomto bodě extrém nevystupuje. Bude-li řád první nenulové derivace ve stacionárním bodě sudý, pak účelová funkce má v tomto bodě lokální extrém, který je ostrým lokálním minimem, resp. maximem, bude-li tato derivace kladná (účelová funkce je ryze konvexní), resp. záporná (účelová funkce je ryze konkávní).“

Při řešení praktických optimalizačních úloh nezávisle proměnná X se obyčejně může měnit v určitém předem daném uzavřeném intervalu . Optimalizační úloha spočívá v nalezení bodů patřících do množiny přípustných řešení , ve kterých účelová funkce f(x) nabývá nejmenší, resp. největší možné hodnoty, tj. bodů globálního minima, resp. maxima. Tato úloha se zapisuje ve tvaru

resp.

Protože v krajních bodech uzavřeného intervalu  vždy vystupují lokální extrémy, je nutno o tyto body rozšířit počet podezřelých bodů. Typ lokálního extrému lze zjistit některou z výše uvedených tří metod s tím, že se uvažuje průnik okolí krajního bodu s množinou přípustných řešení . U spojité účelové funkce body lokálního minima a maxima se střídají – mezi dvěma lokálními minimy je lokální maximum a opačně – mezi dvěma lokálními maximy se nachází vždy lokální minimum. Globální extrém požadovaného druhu se z odpovídajících lokálních extrémů určí vzájemným srovnáním.

Při optimalizaci účelových funkcí jedné proměnné je velmi vhodné si nakreslit alespoň přibližný průběh dané účelové funkce. Značně se tím usnadní řešení optimalizační úlohy a také se zmenší možnost výskytu chyby.

Příklad 2.1

Analyticky vyřešte optimalizační úlohu

Řešení:

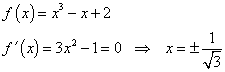
Vzhledem k přípustné množině  význam má pouze stacionární bod .

Účelová funkce f(x) je ryze konvexní, a proto v bodě  nabývá svého ostrého globálního minima.

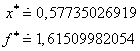
V krajních bodech x = 0 a x = 1 účelová funkce f(x) má ostrá lokální maxima.

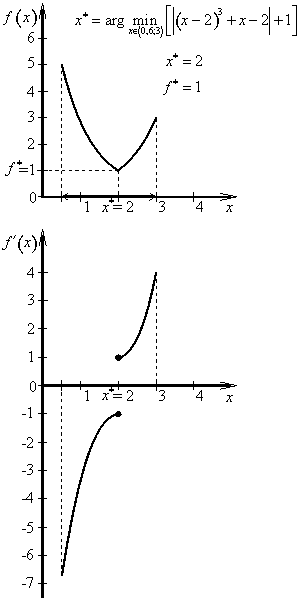
Příklad 2.2

Optimalizační úloha má tvar

Řešení:

Z nutných podmínek dostaneme podezřelé body: x₁ = 0,6; x₂ = 2 a x₃ = 3.

Vypočteme první derivaci f '(x) :

a) 

b) 

V bodě x₂ = 2 první derivace neexistuje (nespojitost prvního druhu). Metodou srovnání znamének první derivace lze zjistit, že v podezřelém bodě x₂ = 2 vystupuje ostré lokální minimum, které je zároveň ostrým globálním minimem:

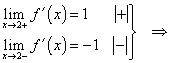 ostré lokální minimum v bodě

x^* = 2
f ^* = 1

V krajních bodech x₁ = 0,6 a x₃ = 3 vystupují ostrá lokální maxima.

Příklad 2.3

Je třeba vyřešit optimalizační úlohu

Řešení:

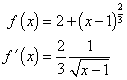
První derivace f '(x) neexistuje a v bodě x₂ = 1 (nespojitost druhého druhu). Podezřelé body: x₁ = 0, x₂ = 1 a x₃ = 3. Budeme-li se blížit k bodu x₂ = 1 zleva, znaménko první derivace f '(x) bude záporné (–) a opačně, budeme-li se blížit k bodu x₂ = 1 zprava, první derivace f '(x) bude kladná (+), a proto v tomto bodě vystupuje ostré lokální minimum, které je zároveň ostrým globálním minimem.

x^* = 1
f ^* = 2

V krajních bodech x₁ = 0 a x₃ = 3 vystupují ostrá lokální maxima.