2. Matematické modely
Uvažujme lineární diskrétní systém (obr. 2. 1).

Stejně jak u spojitých systémů tak i u diskrétních systémů existuje několik možností způsobu vnějšího popisu chování, které vyjadřují vztah mezi výstupní veličinou y(kT) a diskrétní vstupní veličinou u(kT). Vnitřní popis chování diskrétního systému obsahuje kromě uvedených veličin i diskrétní stavové veličiny.
2.1 Popis v časové oblasti – diferenční rovnice systému
Pro popis vlastností dynamického systému v časové oblasti může sloužit diferenční rovnice v normálním tvaru s počátečními podmínkami.
 |
(2.1) |
Klidový ustálený stav (jestliže existuje) je pospán vztahy
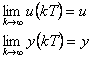 |
(2.2) |
tj. pro 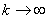 platí
platí
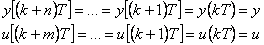 |
Po úpravě dostaneme
 |
(2.3) |
kde 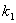 je koeficient přenosu.
je koeficient přenosu.
Diferenční rovnice (2. 1) je lineární, její koeficienty jsou konstantní, hovoříme tedy o stacionárním diskrétním lineárním dynamickém systému.
Statická charakteristika, tedy závislost výstupní veličiny na vstupní veličině v ustáleném stavu je pospána vztahem (2. 3).
Pokud má diferenční rovnice (2. 1) popisovat reálný dynamický systém musí být splněny podmínky fyzikální realizovatelnosti.
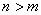 |
Silná podmínka fyzikální realizovatelnosti | |
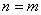 |
Slabá podmínka fyzikální realizovatelnosti | (2. 4) |
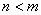 |
Fyzikálně nerealizovatelný systém |
2.2 Popis v oblasti komplexní proměnné – diskrétní přenos
Po Z-transformaci diferenční rovnice (2. 1) získáme přenos ve tvaru podílu Z-obrazu (1. 4) výstupního signálu y(kT) k Z-obrazu vstupního signálu u(kT) při nulových počátečních podmínkách.
 |
(2.5) |
Statická charakteristika (jestliže existuje) je pospána vztahem
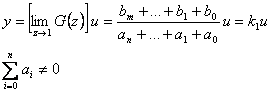 |
(2.6) |
Jmenovatel přenosu G(z) je charakteristický mnohočlen diskrétního lineárního dynamického systému.
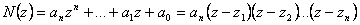 |
(2.7) |
kde 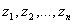 jsou kořeny charakteristické rovnice.
jsou kořeny charakteristické rovnice.
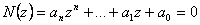 |
(2.8) |
které nazýváme póly přenosu G(z).
Podmínky fyzikální realizovatelnosti jsou dány vztahy (2. 4).
2.3 Popis v kmitočtové oblasti
Pro popis systému je možno také užít diskrétní kmitočtový přenos
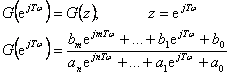 |
(2.9) |
který se používá pro kmitočet
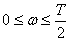 |
Statická charakteristika (jestliže existuje) je pospána vztahem
 |
(2.10) |
Podmínky fyzikální realizovatelnosti jsou dány vztahy (2. 4).
2.4 Popis v časové oblasti – přechodová funkce
Přechodová funkce je odezva dynamického systému na vstupní veličinu ve tvaru Heavisideova jednotkového skoku  .
.
Z-obraz diskrétního jednotkového Heavisideova skoku je
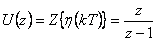 |
(2.11) |
Diskrétní přechodová funkce tedy bude mít tvar
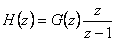 |
(2.12) |
Originál tedy je dán vztahem
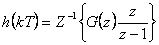 |
(2.13) |
Statická charakteristika (jestliže existuje) je pospána vztahem
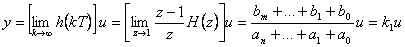 |
(2.14) |
Podmínky fyzikální realizovatelnosti jsou tedy
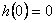 |
Silná podmínka fyzikální realizovatelnosti |
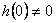 |
Slabá podmínka fyzikální realizovatelnosti |
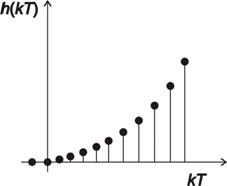
Příklad diskrétní přechodové charakteristiky je na obr. 2. 2.
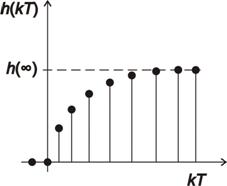
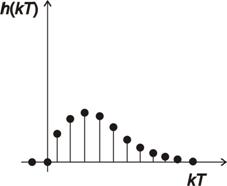
2.5 Popis v časové oblasti – impulsní funkce
Diskrétní impulsní funkce g(kT) je odezva dynamického systému diskrétní jednotkový Diracův impuls  . Z-obraz diskrétního jednotkového Diracova impulsu je
. Z-obraz diskrétního jednotkového Diracova impulsu je
 |
(2.15) |
Diskrétní impulsní funkce je definovaná vztahem
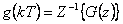 |
(2.16) |
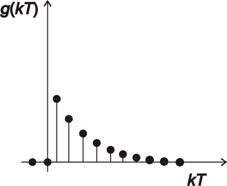
Příklad diskrétní impulsní charakteristiky je na obr. 2. 3.
Statická charakteristika (jestliže existuje) je pospána vztahem
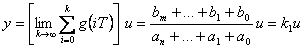 |
(2.17) |
Podmínky fyzikální realizovatelnosti jsou tedy
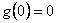 |
Silná podmínka fyzikální realizovatelnosti |
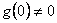 |
Slabá podmínka fyzikální realizovatelnosti |
2.6 Vztah mezi přechodovou a impulsní funkcí
Stejně jako u spojitých systémů, také u diskrétních systémů existuje spojitost mezi přechodovou a impulsní funkcí.
Ze vztahu pro obraz přechodové funkce (2. 18) vypočteme obraz impulsní funkce (2. 19)
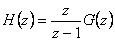 |
(2.18) |
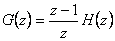 |
(2.19) |
Použitím vlastností Z-transformace z tab 1. 1 dostaneme vztahy (2. 20) a (2. 21). Impulsní funkce je tedy dána zpětnou diferencí přechodové funkce (2. 20), přechodovou funkci získáme sumací impulsní funkce (2. 21).
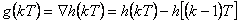 |
(2.20) |
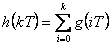 |
(2.21) |
2.7 Stavový popis
Stavový model pro diskrétní lineární dynamický systém má tvar
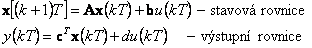 |
(2.22) |
kde
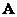 – matice systému (stavová matice systému), rozměr (n x n), – matice systému (stavová matice systému), rozměr (n x n), |
|
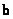 – vektor řízení (stavový vektor řízení), rozměr (n x 1), – vektor řízení (stavový vektor řízení), rozměr (n x 1), |
|
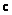 – výstupní vektor (výstupní vektor systému), rozměr (n x 1), – výstupní vektor (výstupní vektor systému), rozměr (n x 1), |
|
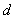 – vektor převodu (výstupní vektor řízení), rozměr (1 x 1). – vektor převodu (výstupní vektor řízení), rozměr (1 x 1). |
Statická charakteristika (jestliže existuje) je pospána vztahem
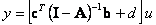 |
(2.23) |
Podmínky fyzikální realizovatelnosti jsou tedy
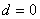 |
Podmínka silné fyzikální realizovatelnosti |
 |
Podmínka slabé fyzikální realizovatelnosti |
Máme-li diskrétní systém pospaný vnějším popisem, resp. diferenční rovnicí (2. 24) nebo diskrétním obrazovým přenosem G(z) (2. 25)
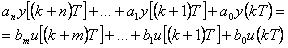 |
(2.24) |
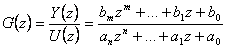 |
(2.25) |
je možno jej převést na vnitřní popis, resp. stavový popis a to několika metodami a to např. [Noskievič, 1992]:
- metodou postupné integrace,
- metodou snižování řádu derivace,
- rozkladem přenosu na dílčí přenosy.
Tak jako je možno vnější popis systému, resp. obrazový přenos G(z) převádět na vnitřní popis, resp. stavový popis, existuje i možnost zpětné operace, tedy převodu ze stavového popisu na obrazový přenos (2. 26).
 |
(2.26) |
2.8 Dělení doskrétních dynamických systémů
Diskrétní dynamické systémy lze rozdělit na tři typy těchto systémů a to P (proporcionální), S (sumační) a D (diferenční). Typ systémů lze určit ze statické charakteristiky, obrazového přenosu G(z) a průběhu přechodové charakteristiky  .
.
Pro připomenutí může být uvedeno, že statická charakteristika je závislost výstupní veličiny y na vstupní veličině u v ustáleném stavu.
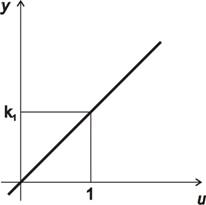
2.8.1 Proporcionální dynamický systém
Statická charakteristika
V případě proporcionálního systému statická charakteristika existuje (obr. 2. 4) a je definovaná
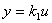 |
(2.27) |
kde
 |
(2.28) |
Obrazový přenos
Při určování typu systému vycházíme z obrazového přenosu G(z) (2. 29).
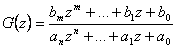 |
(2.29) |
O proporcionální dynamický systém se jedná v případě, že nelze z čitatele ani jmenovatele vytknout výraz 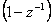 , popř.
, popř. 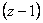 .
.
Přechodová charakteristika
Přechodová charakteristika proporcionálního dynamického systému se ustálí na nenulové konečné hodnotě, resp.
 |
(2.30) |

2.8.2 Sumační dynamický systém
Statická charakteristika
V případě sumačního dynamického systému statická charakteristika neexistuje, protože platí.
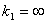 |
(2.31) |
protože platí
 |
(2.32) |
Obrazový přenos
Při určování typu systému opět vycházíme z obrazového přenosu G(z) (2. 33).
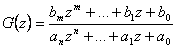 |
(2.33) |
O sumační dynamický systém se jedná v případě, že lze ve jmenovateli vytknout výraz 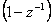 , popř.
, popř. 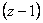 , tedy
, tedy
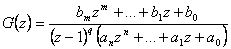 |
(2.34) |
kde q je řád sumace.
Přechodová charakteristika
Přechodová charakteristika sumačního dynamického systému se neustálí, resp.
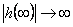 |
(2.35) |
2.8.3 Diferenční dynamický systém
Statická charakteristika
V případě diferenčního systému statická charakteristika existuje, ale je triviální a je rovna
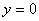 |
(2.36) |
protože platí
 |
(2.37) |

Obrazový přenos
Při určování typu systému opět vycházíme z obrazového přenosu G(z) (2. 38).
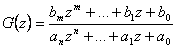 |
(2.38) |
O diferenční dynamický systém se jedná v případě, že lze v čitateli vytknout výraz 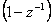 , popř.
, popř. 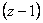 , tedy
, tedy
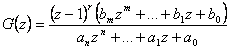 |
(2.39) |
kde r je řád diference.
Přechodová charakteristika
Přechodová charakteristika sumačního dynamického systému se ustálí na hodnotě 0, resp.
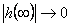 |
(2.40) |
2.9 Matematické modely – řešené příklady
Příklad 2.1
Pro systém popsaný diferenční rovnicí 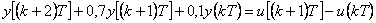 s nulovými počátečními podmínkami
s nulovými počátečními podmínkami 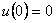 ,
, 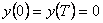 určete:
určete:
- a) obrazový přenos,
- b) přechodovou funkci v uzavřeném tvaru,
- c) impulsní funkci,
- d) vykreslete impulsní a přechodovou charakteristiku pro prvních 5 hodnot,
- e) o jaký typ dynamického systému se jedná a jeho fyzikální realizovatelnost.
Řešení:
- ad a) Určíme obrazový přenos:
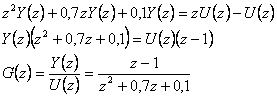
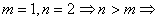 je splněná silná podmínka fyzikální realizovatelnosti.
je splněná silná podmínka fyzikální realizovatelnosti.
- ad b) Pro výpočet diskrétní přechodové funkce použijeme vztah (2. 13):
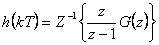
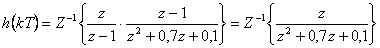
Obraz přechodové funkce rozdělíme na parciální zlomky. Kořeny jmenovatele jmenovatele jsou 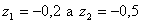 .
.
Nyní lze provést rozklad na parciální zlomky a dosazovací metodou dopočítat koeficienty A, B parciálních zlomků:

Za z dosadíme
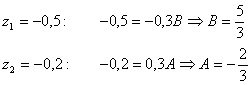
V souladu s tab 1. 2 můžeme psát

pro 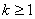 a 0 pro
a 0 pro 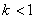 .
.
Nyní vypočteme prvních pět hodnot přechodové charakteristiky:
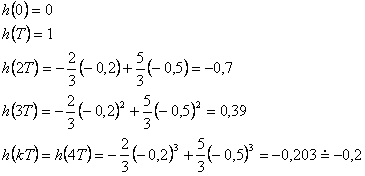
- ad c) Nyní vypočteme prvních pět bodů impulsní charakteristiky s použitím vztahu (2. 20):

- ad d) Dle předešlých výpočtů vykreslíme impulsní a přechodovou charakteristiku pro prvních 5 hodnot:
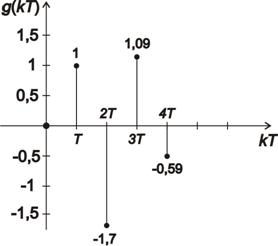
- ad e) Nyní určíme typ dynamického systému a jeho fyzikální realizovatelnost:

Přechodová charakteristika se ustálí v hodnotě 0, z toho vyplývá, že se jedná o diferenční dynamický systém.
Dále je možno říci, že je splněna silná podmínka fyzikální realizovatelnosti, neboť pro obě charakteristiky platí 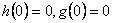 .
.
Příklad 2.2
Pro systém pospaný diferenční rovnicí 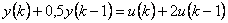 s nulovými počátečními podmínkami
s nulovými počátečními podmínkami 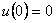 ,
, 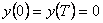 určete:
určete:
- a) obrazový přenos,
- b) přechodovou funkci
- c) impulsní funkci v uzavřeném tvaru,
- d) vykreslete impulsní a přechodovou charakteristiku pro prvních 5 hodnot.
- e) o jaký typ dynamického systému se jedná a jeho fyzikální realizovatelnost.
Řešení:
- ad a) Určíme obrazový přenos:
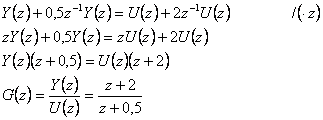
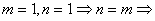 je splněná slabá podmínka fyzikální realizovatelnosti.
je splněná slabá podmínka fyzikální realizovatelnosti.
Vzhledem k požadavku bodu c) v zadání o uzavřeném tvaru impulsní funkce, vypočítáme nejprve tento bod.
- ad c) Určíme impulsní funkci v uzavřeném tvaru:

Nyní vypočteme prvních pět bodů impulsní charakteristiky:
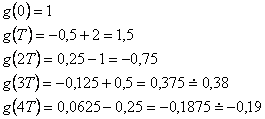
- ad b) S využitím vztahu (2. 21) dopočítáme hodnoty diskrétní přechodové funkce:

- ad d) Dle předešlých výpočtů vykreslíme impulsní a přechodovou charakteristiku pro prvních 5 hodnot:
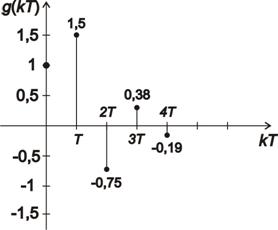
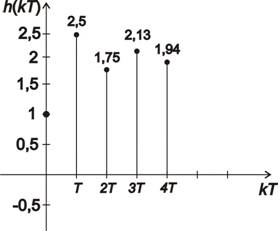
- ad e) Nyní určíme typ dynamického systému a jeho fyzikální realizovatelnost:

Přechodová charakteristika se ustálí na hodnotě 2, z toho vyplývá, že se jedná o proporcionální dynamický systém.
Dynamický systém splňuje slabou podmínku fyzikální realizovatelnosti, neboť obě charakteristiky nezačínají v počátku souřadnicového systému a dále platí n = m = 1.
Příklad 2.3
Pro systém pospaný obrazovým přenosem 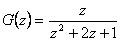 určete:
určete:
- a) impulsní funkci,
- b) přechodovou funkci
- c) vykreslete impulsní a přechodovou charakteristiku pro prvních 5 hodnot.
- d) určete podmínky fyzikální realizovatelnosti a o jaký typ dynamického systému se jedná.
Řešení:
- Převedeme obrazový přenos na diferenční rovnici.

- ad a) Určíme hodnoty diskrétní impulsní funkce:

- ad b) Pro určení hodnot diskrétní přechodové použijeme vztah (2. 21):

- ad d) Dle předešlých výpočtů vykreslíme impulsní a přechodovou charakteristiku pro prvních 5 hodnot:
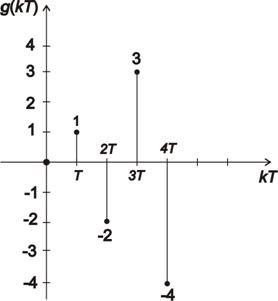
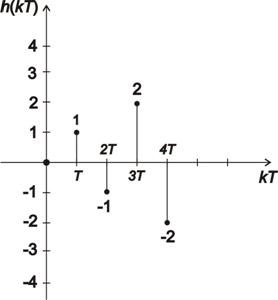
Z průběhu 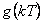 a
a 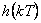 vidíme, že tento dynamický systém je nestabilní.
vidíme, že tento dynamický systém je nestabilní.
- ad e) Nyní určíme typ dynamického systému a jeho fyzikální realizovatelnost:
Protože se jedná o nestabilní systém, jeho typ určíme z přenosu G(z). Ani v čitateli, ani ve jmenovateli přenosu nelze vytknout dvojčlen (z - 1), proto se jedná o proporcionální dynamický systém.
Je splněna silná podmínka fyzikální realizovatelnosti, neboť obě charakteristiky začínají v počátku souřadnicového systému a dále platí n = 2 a m = 1.