<<<< Obsah >>>>

Propustnost dopravní sítě

Používá se:

· při řešení dopravního problému,

· při přepravě nějaké látky a podobně, přičemž je třeba nadimenzovat potrubí (cestu, kabel), kterým proteče jen určité množství látky.

Použijeme vždy neorientovaný ohodnocený graf, kde hrany jsou trasy a uzly jsou křižovatky. Musí být jeden zdroj u (počáteční uzel) a jeden spotřebič v (koncový uzel). Pokud je více zdrojů, je třeba je sloučit do jednoho zdroje a propustnost nových hran se rovná kapacitě dílčích zdrojů. To samé je také u spotřebičů. Každá hrana je ohodnocena takzvanou propustností hrany C(h) a znamená, kolik maximálně může protéct látky.

Tok hranou F(h) je skutečné množství, které hranou proteče

.

Úkolem je určit:

· propustnost celé dopravní sítě C*(u, v), to znamená maximální množství, které může sítí protéct ze zdroje do spotřebiče,

· tok dopravní sítí F(u, v), tj. skutečné množství, které proteče sítí ze zdroje do spotřebiče

.

Dále je třeba udělat z grafu orientovaný acyklický graf. Hrany, kterými neprotéká žádná látka, musíme vyloučit, jinak by mohl vzniknout sací efekt. V každém uzlu platí Kirchhoffovy zákony (platí i pro zdroj a spotřebič).

Hledáme hranový řez mezi uzly u a v.

C (k) – hranový řez

C (k_min) – minimální hodnota hranového řezu

C (k_min) = C*(u,v)

Hranový řez mezi uzly u a v v souvislém neorientovaném grafu G je taková množina hran K, pro které platí:

· Graf G, který má množinu hran zmenšenou o K , má právě dvě komponenty, přičemž uzel u leží v jedné z nich a uzel v leží v druhé.

· Je-li množina hran K´ podmnožinou množiny K (K´Ì K a zároveň K´¹ K), pak v grafu G, který má množinu hran K´, existuje sled mezi uzly u a v.

Metody k určení minimálního hranového řezu C (k_min)

a) Metoda dolní cesty

· Úprava grafu na jeden zdroj a jeden spotřebič.

· Překreslení grafu tak, aby uzly u a v ležely na hranici grafu.

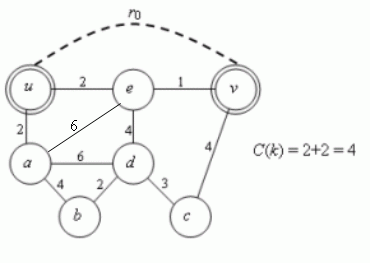
Obr. 3.34 Zavedení pomocné hrany r₀

· Zavedeme pomocnou hranu r₀ s ohodnocením nula, která rozdělí graf na dvě oblasti E₁ a E₂

· Na hranici oblasti E₁ vybereme hranu s nejmenším ohodnocením a tuto hranu vynecháme, zvětší se oblast E₂.

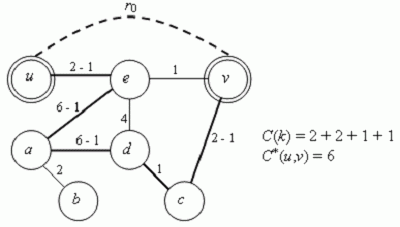
· Ohodnocení vypuštěné hrany se zapíše do hranatého řezu a graf překreslíme (viz obr. 3.35) tak, abychom snížili krajní hrany, které sousedily s E₁ o hodnotu vypuštěné hrany.

Obr. 3.35 Ohodnocení vypuštěné hrany

· Toto opakujeme tak dlouho, až se nám graf rozpadne na dvě komponenty.

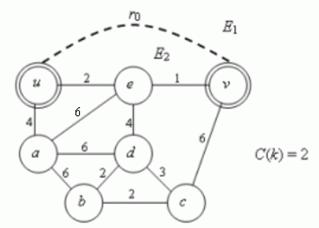
· Pokud je více hran se stejným ohodnocením, vypustíme všechny hrany, ale do hranového řezu zapíšeme pouze jednu (viz obr. 3.36 a obr. 3.37).

Obr. 3.36 Vypuštění hran se stejným ohodnocením

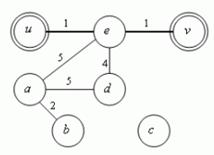
Obr. 3.37 Výsledný graf

b) Metoda vytvoření duálního grafu

Sestrojení duálního grafu G^D: Do každé oblasti grafu umístíme jeden uzel a pro každou hranu K sestrojíme hranu K^D spojující uzly duálního grafu G^D, které odpovídají oblastem grafu G incidentním s hranou K. Oblast grafu je uzavřená část grafu vymezená hranami.

První krok: Graf rozdělíme na oblasti.

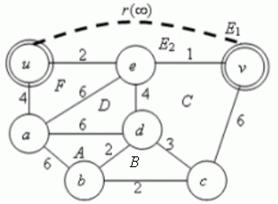
Obr. 3.38 Rozdělení grafu na oblasti

Druhý krok: Stávající graf překreslíme do duálního grafu - oblasti se stávají uzly.

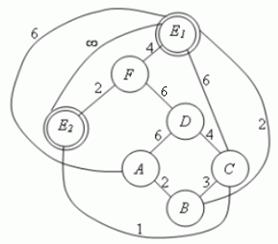
Obr. 3.39 Výsledný duální graf

Hledáme minimální cestu z E₁ do E₂ a to je:

C (k_min) .

Typy úloh

· dopravní úlohy (kapacita silnic, rozvod vody, plynu a podobně),

· přiřazovací úlohy (přiřazení n-úkolů m-pracovníkům),

· jízdní řády.

Zde jsou příklady na procvičení probrané látky. Propustnost dopravní sítě.

<<<< Nahoru >>>>