Teorie pravděpodobnosti
Základní pojmy
Pokus je každá realizace určitého předem stanoveného komplexu podmínek [Kába, B., 1999]. Pokus musí být reprodukovatelný, to znamená:
· je nutno, aby podmínky, za nichž pokus probíhá, byly stabilizovány,
· existuje alespoň teoretická možnost opakování pokusu,
· výsledek pokusu není předem znám (výsledek není jednoznačně určen jeho podmínkami), je to však právě jeden z prvků známé množiny výsledků, kterou nazýváme základní prostor (možné výsledky náhodného pokusu).
Jev je každý fakt, o kterém, jakožto o výsledku pokusu, má smysl prohlásit, zda nastal nebo nenastal.
Typy jevů:
· jev jistý - vždy nastane při daném komplexu podmínek,
· jev nemožný - nikdy nenastane při daném komplexu podmínek,
· jev náhodný - může a nemusí nastat při daném komplexu podmínek.
Další pojmy
Opačný jev
Jev, který spočívá v nenastoupení jevu A je jev opačný k jevu A, značí se ![]() (A negace).
(A negace).
![]()
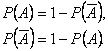
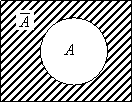
Obr. 2.1 Opačný jev
Průnik jevů ![]()

Obr. 2.2 Průnik jevů
Sjednocení jevů ![]()

Obr. 2.3 Sjednocení jevů
Relativní četnost:
je definována jako poměr počtu pokusů příznivých danému jevu m ku počtu všech pokusů n:
![]() .
.
Statistická definice pravděpodobnosti
Vychází se z experimentálního zjištění, že při zvětšování počtu pokusů n ® ¥ se relativní četnost určitého jevu P* blíží k určité konstantní hodnotě, kterou nazveme pravděpodobností jevu A [Kába, B., 1999]
![]()
Klasická definice pravděpodobnosti
Pravděpodobnost jevu A je rovna počtu m možných výsledků pokusů příznivých jevu A k počtu n všech možných výsledků pokusu [Kába, B., 1999]:
![]()
Za předpokladu, že všechny výsledky jsou stejně možné a jsou všechny, n je konečné číslo.
Axiomatická definice pravděpodobnosti (A. N. Kolmogorov, 1933)
a) ![]() ,
,
b) pravděpodobnost nemožného jevu A je rovna nule [P(A) = 0],
c) pravděpodobnost jistého jevu A je rovna jedné [P(A) = 1],
d) A1, A2,…, An jsou po dvou neslučitelné jevy, to znamená, nikdy nemohou nastat současně dva z těchto jevů, potom platí
![]()
Tato kapitola je podrobně popsána v literatuře [Kába, B., 1999].