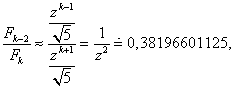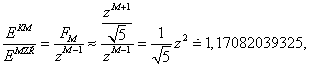2 Statická optimalizace funkcí jedné proměnné

2.3 Zhodnocení metod jednorozměrné optimalizace

Metody jednorozměrné optimalizace mají v celé teorii optimalizace základní význam. Jsou velmi názorné, mají jednoduchou grafickou interpretaci a hlavně – využívají se i ve vícerozměrné optimalizaci.

Analytické metody umožňují získat jak kvantitativní výsledky, tak i kvalitativní údaje při změnách některých parametrů. Proto, pokud to daná optimalizační úloha dovoluje, je třeba vždy použít především analytických metod řešení.

Numerické metody dávají číselné hodnoty pro konkrétní hodnoty parametrů optimalizační úlohy.

Bolzanova metoda je velmi jednoduchá a má velmi malé požadavky na optimalizovanou účelovou funkci. Svou podstatou je blízká postupným komparativním metodám, ale vyžaduje určování první derivace.

Newtonova metoda je vhodná pro ryze konvexní (konkávní) účelové funkce, u kterých lze snadno vypočíst první a druhou derivaci (derivace musí být spojité). Konvergence je velmi rychlá, ale požadavky na vlastnosti účelové funkce jsou velmi ostré.

Metoda sečen nemá tak ostré požadavky na účelovou funkci jako Newtonova metoda, ale její konvergence je značně pomalejší. Často se obě metody kombinují.

Metoda kvadratické interpolace je velmi jednoduchá. S výhodou se kombinuje s metodou zlatého řezu, pomocí které se nejdříve zlokalizuje optimální bod v nějakém malém intervalu neurčitosti a pak se jeho poloha upřesní metodou kvadratické interpolace.

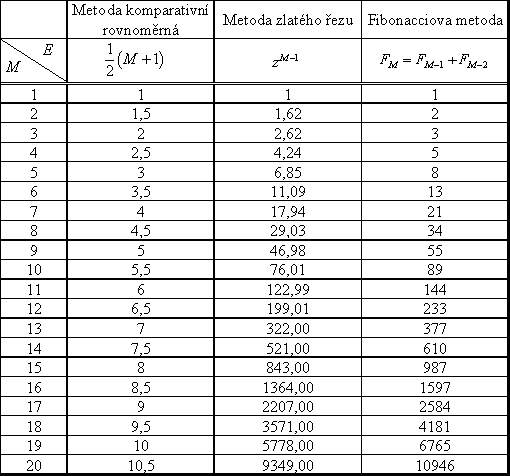
Komparativní metody patří k nejuniverzálnějším metodám jednorozměrné optimalizace. Jejich jediným požadavkem na účelovou funkci je unimodalita (v našem případě ještě spojitost). Svými vlastnostmi umožňují i experimentální optimalizaci, což je z praktického hlediska velmi důležité. Experimentální optimalizace se běžně provádí nepostupnými komparativními metodami, např. rovnoměrnou komparativní metodou. Takový přístup k experimentální optimalizaci je však neefektivní. Nepostupných metod používáme pouze tehdy, když všechny experimenty je nutno provádět současně (paralelně), jinak vždy použijeme některou z postupných komparativních metod. Lze tak podstatně snížit počet nákladných měření (viz tab 2.2).

V tabulce 2.2 jsou uvedeny efektivnosti základních komparativních metod pro různý počet experimentů.

Fibonacciova metoda je optimální postupnou komparativní metodou. Její velikou vadou je nutnost znalosti počtu kroků N, resp. počtů experimentů M před zahájením výpočtu. Tento problém vystupuje v těch případech, kdy není omezen počet experimentů M a kritériem zakončení výpočtu místo zaručené přesnosti určení optimálního bodu x^* je přesnost vyznačení optimální hodnoty účelové funkce f ^*.

Mezi metodou zlatého řezu a Fibonacciovou metodou existuje úzká souvislost.

Pro veliká k totiž platí [viz (2.73)]:

tj. pro veliká N , resp. M obě metody začínají ve stejných počátečních bodech  a . Proto je možno začít výpočet metodou zlatého řezu a když je už interval neurčitosti dostatečně malý, určit N a přejít k Fibonacciově metodě.

Protože metoda zlatého řezu je jenom o okolo 17 % horší než Fibonacciova metoda, což plyne ze vztahu

proto metoda zlatého řezu je v praxi nejvíce používána.

U obou metod počet kroků N nemůže být příliš veliký, protože díky zaokrouhlování může dojít k numerické nestabilitě. Doporučuje se volit

resp. na každém kroku určit vždy dva nové body (a ne jeden), aby chyby zaokrouhlování nezpůsobily ztrátu intervalu neurčitosti obsahujícího optimální bod x^*.