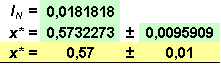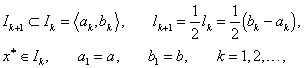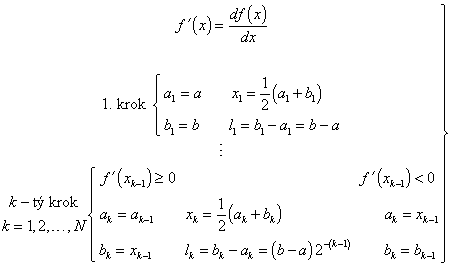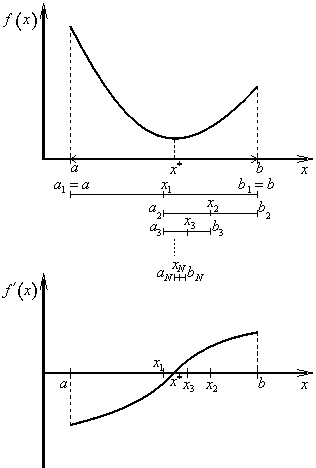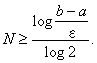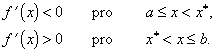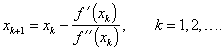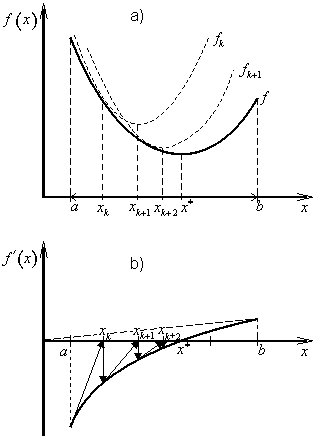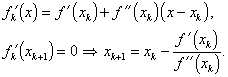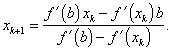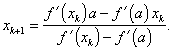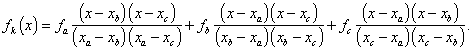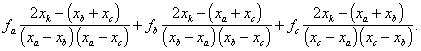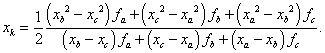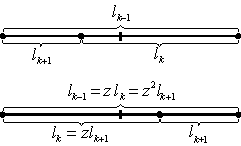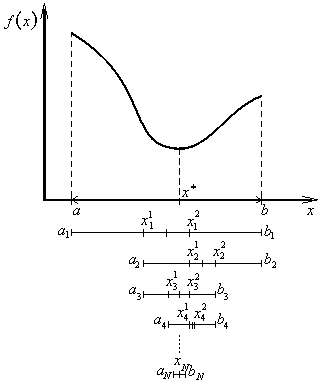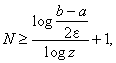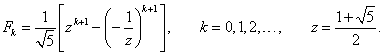2 Statická optimalizace funkcí jedné proměnné

2.2 Numerické metody jednorozměrné optimalizace

Numerické metody jednorozměrné optimalizace lze rozdělit na dvě základní skupiny:

diferenciální (gradientní) metody – vyžadují určování hodnot účelové funkce a její první, resp. druhé derivace
přímé metody – vyžadují pouze určování hodnot účelové funkce.

Budeme se zde zabývat numerickými metodami jednorozměrné minimalizace spojitých unimodálních funkcí (jsou to takové funkce, které mají jeden extrém na daném intervalu), tj. řešením optimalizační úlohy

(2.5)

(2.6)

Není-li daná účelová funkce f(x) na intervalu unimodální, pak je třeba přibližně určit polohu bodu globálního minima a interval zmenšit tak, aby na zmenšeném intervalu účelová funkce f(x) byla unimodální.

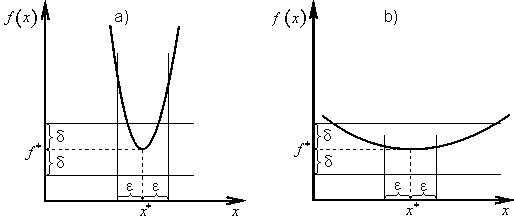
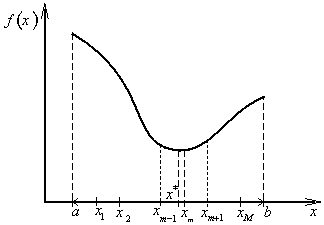
U numerických metod je nutno předem zadat požadovanou přesnost vyznačení optimálního řešení x^*, tj. nezáporné číslo ε, pro které N-tá aproximace řešení x_N musí vyhovovat nerovnosti

(2.7)

a také požadovanou přesnost vyznačení optimální hodnoty účelové funkce f ^*, tj. nezáporné číslo δ, pro které hodnota účelové funkce v bodě x_N vyhovuje nerovnosti (obr. 2.4)

(2.8)

Obr. 2.4: Přesnost řešení

U některých numerických metod kontrola splnění podmínek (2.7), resp. (2.8) je problematická. Jde především o ty případy, kdy informace o vlastnostech účelové funkce f(x) jsou velmi nedostatečné, proto se rovněž používají vztahy

(2.9)

resp.

(2.10)

2.2.1 Diferenciální metody

Budeme uvažovat hladkou unimodální účelovou funkci f(x) na intervalu mající ostré globální minimum v jediném stacionárním bodě, který je reálným kořenem rovnice

(2.11)

V jednodušších případech lze rovnici (2.11) řešit analyticky. Bude-li tato rovnice transcendentní (nealgebraická), její řešení musíme hledat pomocí numerických iteračních metod.

a) Bolzanova metoda

Nejjednodušší iterační metodou jednorozměrné minimalizace je Bolzanova metoda (metoda půlení intervalu, metoda dichotomie), kterou využijeme pro řešení rovnice (2.11). Bolzanova metoda spočívá v utvoření takové posloupnosti intervalů

(2.12)

pro kterou platí vztahy

(2.13)

kde l_k je délka intervalu I_k.

Ze vztahů (2.13) v limitě dostaneme

(2.14)

(2.15)

Interval I_k nazýváme k-tým intervalem neurčitosti nebo lokalizace.

Bolzanova metoda může být popsána následujícím algoritmem (obr. 2.5):

(2.16)

Obr. 2.5: Princip Bolzanovy metody

Po N-tém kroku optimální bod x^* leží v intervalu neurčitosti I_N a proto lze psát

(2.17)

kde

(2.18)

Nutný počet kroků N při lokalizace optimálního bodu x^* s přesností dostaneme úpravou vztahů (2.17) a (2.18)

(2.19)

V algoritmu (2.16) se využívá vlastnosti hladké unimodální účelové funkce f(x), která může být vyjádřena nerovnostmi

(2.20)

Bolzanova metoda je vždy konvergentní, pokud jsou splněny její podmínky (2.20), ale rychlost konvergence je malá.

Příklad 2.4

Bolzanovou metodou vyřešte optimalizační úlohu z příkladu 2.1 s přesností ε = 0,01

Řešení:

Potřebný počet kroků vypočteme ze vztahu

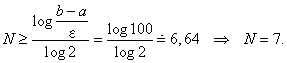
Shodně s algoritmem Bolzanovy metody (2.16) lze psát:

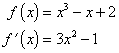
Jednotlivé kroky řešení:

1. krok:	a₁ = a = 0	b₁ = b = 1	x₁ = 0,5	f '(x₁) = -0,25 < 0
2. krok:	a₂ = x₁ = 0,5	b₂ = b₁ = 1	x₂ = 0,75	f '(x₂) = 0,6875 > 0
3. krok:	a₃ = a₂ = 0,5	b₃ = x₂ = 0,75	x₃ = 0,625	f '(x₃) = 0,17188 > 0
4. krok:	a₄ = a₃ = 0,5	b₄ = x₃ = 0,625	x₄ = 0,5625	f '(x₄) = -0,05018 < 0
5. krok:	a₅ = x₄ = 0,5625	b₅ = b₄ = 0,625	x₅ = 0,59375	f '(x₅) = 0,05762 > 0
6. krok:	a₆ = a₅ = 0,5625	b₆ = x₅ = 0,59375	x₆ = 0,57813	f '(x₆) = 0,00269 > 0
7. krok:	a₇ = a₆ = 0,5625	b₇ = x₆ = 0,57813	x₇ = 0,57031

Výsledek zapíšeme:

l₇ = b₇ - a₇ = 0,01563

Přibližné řešení:

Přesné řešení:

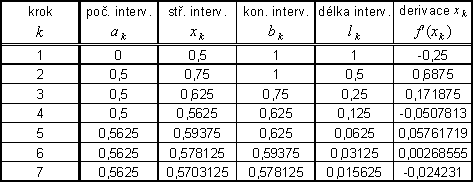
Výsledek řešení ze souboru v Excelu (StatOpt-BolzMet.xls):

b) Newtonova metoda

Mezi základní iterační metody řešení rovnice (2.11) patří Newtonova metoda (Newtonova-Raphsonova metoda, metoda tečen). Tato metoda spočívá v utvoření posloupnosti bodů podle Newtona rekurentního vzorce

(2.21)

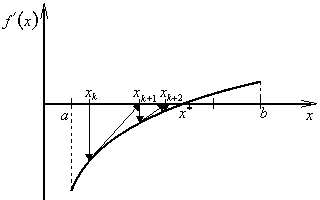
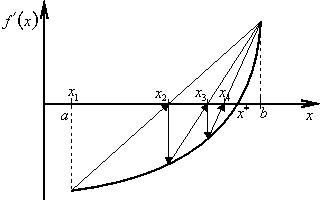
Metoda odpovídá sestrojení tečny v bodě funkce f '(x), viz obr. 2.6. Průsečík tečny s osou X, tj. bod x_k+1 je (k+1)-ní aproximace kořene rovnice (2.11), a tedy i optimálního bodu x^*.

Obr. 2.6: Princip Newtonovy metody

Postačujícími podmínkami konvergence posloupnosti bodů k optimálnímu bodu x^*, tj.

(2.22)

jsou:

(2.23)

(2.24)

(2.25)

Za počáteční aproximaci je vhodné volit takový bod x₁, který vyhovuje nerovnosti

(2.26)

Při nevhodné volbě počátečního bodu x₁ další aproximace může ležet vně intervalu ., viz obr. 2.6b.

Newtonův rekurentní vzorec (2.21) má ještě jednu velmi názornou interpretaci. V okolí bodu x_k účelovou funkci f(x) zastoupíme prvními třemi členy Taylorova rozvoje (kvadratickou parabolou)

(2.27)

Za (k+1)-ní aproximaci optimálního bodu X zvolíme bod x_k+1, ve kterém funkce f_k(x) nabývá svého ostrého globálního minima. Z nutné podmínky dostaneme (obr. 2.6a)

(2.28)

Obdrželi jsme Newtonův rekurentní vzorec (2.21).

Odhad přesnosti N-té aproximace lze provést např. podle vztahu

(2.29)

kde

(2.30)

Konvergence Newtonovy metody je tím rychlejší, čím více se účelová funkce f(x) blíží kvadratické parabole, pro kterou přesné řešení dostaneme po jednom kroku.

Newtonova metoda má některé velmi nepříjemné vady. Nejdůležitější jsou:

příliš tvrdé postačující podmínky konvergence (2.23) – (2.25),
v každé iteraci je třeba počítat první f '(x) a druhou derivaci f ''(x).

V praxi je možno použít modifikaci Newtonovy metody spočívající v tom, že když druhá derivace f ''(x) se již mnoho nemění, lze ji ponechat beze změny i pro následující iterace, tj. použijeme vzorce (obr. 2.7)

(2.31)

kde B je konstanta rovná posledně vypočtené druhé derivaci f ''(x) . Tato modifikovaná metoda se někdy také nazývá Whittakerova metoda.

Obr. 2.7: Princip modifikované Newtonovy metody

U Newtonovy metody se nevypočítává počet kroků iterace a výpočet se ukončí když platí a výsledek se zapíše ve tvaru protože se blížíme k extrému účelové funkce f(x) jen z jedné strany.

Příklad 2.5

Optimalizační úlohu z příkladu 2.1 vyřešte Newtonovou metodou a modifikovanou Newtonovou metodou, obě pro přesnost ε_N = 0,001

Řešení:

a) Newtonova metoda

Nejdříve vypočteme všechny požadované derivace účelové funkce:

f '(x) = 3x² - 1

f ''(x) = 6x

f '''(x) = 6

Zkontrolujeme postačující podmínky konvergence:

f '(0) f '(1) = - 2 < 0,

Postačující podmínky konvergence Newtonovy metody jsou splněny pro polouzavřený interval .

Za počáteční aproximaci volíme bod x₁ = 1, protože platí

f '(1) f '''(1) = 12 > 0.

Newtonův rekurentní vzorec má tvar

x₁ = 1
x₂ = 0,66667
x₃ = 0,58333
x₄ = 0,57738
x₅ = 0,57735

|x₅ - x₄| = 0.00003

Přibližné řešení:

b) modifikovaná Newtonova metoda

Ve vzorci (2.31) za B volíme f ''(1) = 6 a dostaneme:

x₁ = 1
x₂ = 0,66667
x₃ = 0,61111
x₄ = 0,59105
x₅ = 0,58305
x₆ = 0,59974
x₇ = 0,57836
x₈ = 0,57778

|x₈ - x₇| = 0.00058

Přibližné řešení:

Přesné řešení:

c) Metoda sečen

Tato metoda vychází z Newtonovy metody a proto pro ni platí stejné postačující podmínky konvergence (2.23) – (2.25).

Zastoupíme-li v Newtonově rekurentním vzorci (2.21) směrnici tečny funkce f '(x) v bodě x_k [tj. výraz f ''(x_k)] směrnicí vhodně volené sečny, např.

(2.32)

(2.33)

pak dostaneme vztah pro metodu sečen

(2.34)

Metoda sečen má několik modifikací. Vztahy (2.32) – (2.34) vyjadřují případ uvedený na obr. 2.8, kdy pevným bodem je bod b a platí pro něj

Obr. 2.8: Princip metody sečen

Pokud to neplatí, bude pevným bodem bod a a vztah (2.34) je třeba upravit na tvar

Vhodnou volbou počátečních aproximací lze u této metody zajistit konvergenci u většiny praktických případů. Rychlost konvergence je pomalejší než u Newtonovy metody. Ukončení iteračního výpočtu a zápis řešení optimalizační úlohy je stejný jako u Newtonovy metody. Výsledek zapisujeme ve tvaru kde pro x_k+1 platí kde ε je zadaná přesnost.

S výhodou se využívá kombinace metody sečen s Newtonovou metodou.

Příklad 2.6

Metodou sečen je třeba řešit optimalizační úlohu z příkladu 2.1 s přesností ε_N = 0,001

Řešení:

Zvolíme si b = 1 a shodně se vztahem (2.34) pro f '(x) = 3x² - 1 dostaneme:

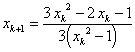
x₁ = 1
x₂ = 0,33333
x₃ = 0,5
x₄ = 0,55556
x₅ = 0,57143
x₆ = 0,57576
x₇ = 0,57692
x₈ = 0,57724

|x₈ - x₇| = 0,00032

Přibližné řešení:

Přesné řešení:

2.2.2 Přímé metody

a) Metoda kvadratické interpolace

Metoda kvadratické interpolace spočívá v aproximaci hladké unimodální účelové funkce f(x) v okolí minima kvadratickou parabolou (mnohočlenem 2. stupně). Předpokládejme, že známe hodnoty účelové funkce f(x) ve třech bodech x_a < x_b < x_c . Označíme je f_a, f_b a f_c. Použijeme Lagrangeův interpolační mnohočlen, který pro tento případ má tvar

(2.35)

Aproximační kvadratická parabola f_k(x) má ostré globální minimum ve stacionárním bodě x_k, který je jediným reálným kořenem rovnice

(2.36)

tj.

(2.37)

Odtud dostaneme

(2.38)

Pro ekvidistantní body (body stejně vzdálené od sebe) x_a, x_b a x_c, tj. pro

(2.39)

vztah (2.38) se podstatně zjednoduší

(2.40)

Při řešení úloh jednorozměrné minimalizace metodou kvadratické interpolace se nejčastěji postupuje dvojím způsobem:

a)Vypočtený bod x_k je dosazen ve vzorci (2.38) na místo jednoho ze tří bodů x_a, x_b nebo x_c, a počítá se další aproximace x_k+1.

b)Body x_a, x_b a x_c jsou voleny tak, aby byly splněny podmínky (2.39) a

(2.41)

Vypočtený bod x_k ze vztahu (2.40) se dosadí za bod x_b a další body x_c a x_a, jsou vybrány takovým způsobem, aby vyhovovaly podmínkám (2.39), (2.41) a počítá se další aproximace x_k+1, tj.

(2.42)

Rozdíl se na každém kroku vhodně zmenšuje.

Problém konvergence metody kvadratické interpolace je velmi složitý a závisí především na vhodné volbě bodů x_a, x_b a x_c.

U této metody se nevypočítává počet kroků iterace a výpočet se ukončí když platí a výsledek se zapíše ve tvaru

Příklad 2.7

Úlohu minimalizace z příkladu 2.1 vyřešte metodou kvadratické interpolace

Řešení:

K výpočtu použijeme vzorec (2.40), resp. (2.42).

Volíme body:

x_a = a = 0	f_a = 2
x_b = 0,45
x_c = 0,9	f_c = 1,82900

Nemůžeme volit např. body:

x_a = a = 0	f_a = 2
x_b = 0,5
x_c = b = 1	f_c = 2

protože f_c - f_a = 0.

Po dosazení do (2.40) dostaneme:

Volíme další body, např.:

x_a₁ = 0,42	f_a₁ = 1,65409
x_b₁ = x₁ = 0,52
x_c₁ = 0,62	f_c₁ = 1,61833

Ze vzorce (2.42) dostaneme:

x₂ = 0,57731

Přibližné řešení:

Přesné řešení:

b) Rovnoměrná komparativní metoda

Rovnoměrná komparativní metoda (metoda rovnoměrného hledání) patří mezi nepostupné (pasivní) komparativní metody hledání minima libovolné spojité unimodální účelové funkce f(x). U této metody počáteční interval neurčitosti rozdělíme body

(2.43)

a vyhledáme (obr. 2.9)

(2.44)

Obr. 2.9: Princip rovnoměrné komparativní metody

Optimální bod x^* je lokalizován v intervalu neurčitosti a proto lze psát

(2.45)

U komparativních metod určení hodnoty účelové funkce f(x) výpočtem nebo experimentálním měřením se nazývá experiment. Efektivnost těchto metod vyjadřuje poměr délky počátečního intervalu neurčitosti k délce posledního N-tého intervalu neurčitosti při stejném počtu experimentů M , tj.

(2.46)

Počet experimentů M u rovnoměrné komparativní metody při požadované přesnosti ε lze určit z nerovnosti

(2.47)

ze které po úpravě dostaneme

(2.48)

Shodně se vztahy (2.46) a (2.47) efektivnost rovnoměrné komparativní metody je

(2.49)

c) Metoda zlatého řezu

Metoda zlatého řezu patří mezi postupné (adaptivní) komparativní metody hledání minima libovolné spojité unimodální účelové funkce f(x). Postupné komparativní metody spočívají, podobně jako Bolzanova metoda, v utvoření takové posloupnosti intervalů neurčitosti , která vyhovuje vztahům

(2.50)

(2.51)

Každý následující interval neurčitosti je podintervalem předcházejícího intervalu neurčitosti, a proto posloupnosti a konvergují:

(2.52)

(2.53)

Počet kroků N je dán požadovanou přesností ε, pro kterou platí vztahy:

(2.54)

(2.55)

kde

(2.56)

Metoda zlatého řezu spočívá v rozdělení každého intervalu neurčitosti tak, aby poměr větší části k menší byl roven poměru celého děleného intervalu k větší části (obr. 2.10), tj.

(2.57)

(2.58)

Obr. 2.10: Rozdělení intervalu v metodě zlatého řezu

Po dosazení (2.57) do (2.58) a úpravě dostaneme kvadratickou rovnici

(2.59)

jejíž kladný kořen je hledaný poměr

(2.60)

Platí pro něj vztahy:

(2.61)

(2.62)

(2.63)

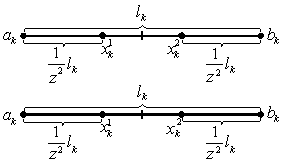
Při metodě zlatého řezu ve všech krocích (kromě prvního) interval neurčitosti obsahuje spolu s krajními body jeden vnitřní bod. Proto je třeba určit hodnotu účelové funkce f(x) pouze v jednom novém bodě umístěném symetricky k již známému bodu (obr. 2.11 a obr. 2.12).

Obr. 2.11: Rozdělení intervalu metodou zlatého řezu v k-tém kroku

Obr. 2.12: Princip metody zlatého řezu

Metodu zlatého řezu lze popsat algoritmem:

(2.64)

Po N -tém kroku optimální bod x^* je lokalizován v intervalu neurčitosti o délce

(2.65)

tj.

(2.66)

Potřebný počet kroků N pro určení optimálního bodu x^* s přesností ε zjistíme ze vzorce

(2.67)

který získáme úpravou vztahů (2.54) a (2.65). Počet experimentů M je stejný jako počet kroků N, tj.

(2.68)

Efektivnost metody zlatého řezu je dána vztahem [viz (2.46) a (2.65)]

(2.69)

U metody zlatého řezu se výsledek zapíše ve tvaru

Příklad 2.8

Úlohu minimalizace z příkladu 2.1 vyřešte metodou zlatého řezu s přesností ε = 0,01

Řešení:

Počet kroků vypočteme ze vzorce (2.67)

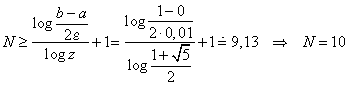
Shodně s algoritmem (2.64) pro lze psát:

1. krok:	a₁ = a = 0
	b₁ = b = 1
2. krok:
	b₂ = b₁ = 1
3. krok:

4. krok:

5. krok:

6. krok:

7. krok:

8. krok:

9. krok:

10. krok:		x₁₀ = 0,57703	l₁₀ = 0,01316

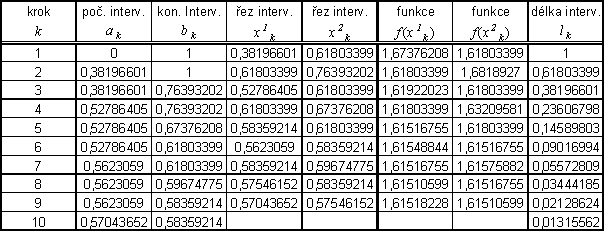
Přibližné řešení:

Zápis výsledku s ohledem na zadanou přesnost ε:

Přesné řešení:

Výsledek řešení ze souboru v Excelu (StatOpt-MetZlatRezu.xls):

d) Fibonacciova metoda

Fibonacciova (Kieferova) metoda rovněž patří mezi postupné komparativní metody, a proto pro ni platí vztahy (2.50) – (2.56). Fibonacciova metoda využívá při zkracování intervalů neurčitosti přímé úměrnosti jejich délek číslům Fibonacciovy posloupnosti (obr. 2.13), tj.

(2.70)

kde čísla Fibonacciovy posloupnosti jsou dány vztahy

(2.71)

resp.

(2.72)

Obr. 2.13: Dělení intervalu u Fibonacciovy metody

Pro veliké k lze v rovnici (2.72) výraz zanedbat a dostaneme přibližný vzorec pro výpočet čísel Fibonacciovy posloupnosti

(2.73)

V tabulce 2.1 je uvedeno prvních 16 čísel Fibonacciovy posloupnosti a také jejich aproximace podle vztahu (2.73).

Tab. 2.1: Prvních 16 čísel Fibonacciovy posloupnosti

Fibonacciova metoda minimalizace může být popsána následujícím algoritmem:

(2.74)

Malé kladné číslo γ na N-tém kroku dovoluje určit polohu optimálního bodu x^* vzhledem k bodu x_N-1 . Hodnotu čísla γ volíme nejméně o řád menší než je požadovaná přesnost ε. Po N-tém kroku optimální bod x^* leží v intervalu a proto lze psát

(2.75)

(2.76)

Pro dosažení přesnosti ε při lokalizaci optimálního bodu x^* ze vztahů (2.54) a (2.76) dostaneme

(2.77)

tj. musíme najít takové číslo Fibonacciovy posloupnosti, které vyhovuje nerovnosti (2.77). Jeho index N udává počet potřebných kroků, a zároveň počet experimentů M , tzn.

(2.78)

Využijeme-li v nerovnosti (2.77) aproximace (2.73), pak dostaneme přibližný vztah

(2.79)

Pro efektivnost Fibonacciovy metody platí [viz vztah (2.76) a (2.78)]

(2.80)

resp. přibližně

(2.81)

U Fibonacciovy metody číslo N musíme znát před zahájením výpočtu.

Příklad 2.9

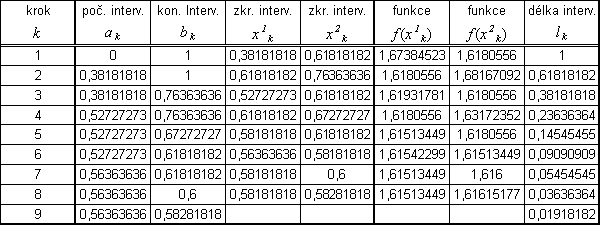
Úlohu minimalizace z příkladu 2.1 řešte Fibonacciovou metodou s přesností ε = 0,01

Řešení:

Počet kroků N zjistíme ze vztahu (2.77), resp. (2.79):

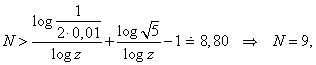
Shodně s algoritmem Fibonacciovy metody lze psát:

1. krok:	a₁ = a = 0
	b₁ = b = 1
2. krok:
	b₂ = b₁ = 1
3. krok:

4. krok:

5. krok:

6. krok:

7. krok:

8. krok:

9. krok:	a₉ = x₈ = 0,56364	x₉ = 0,57323
	b₉ = b₈ = 0,58282

Přibližné řešení:

Zápis výsledku s ohledem na zadanou přesnost ε:

Přesné řešení:

Výsledek řešení ze souboru v Excelu (StatOpt-FibonacMet.xls):