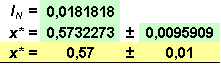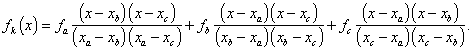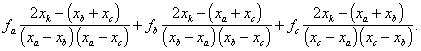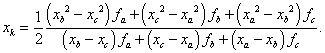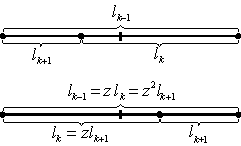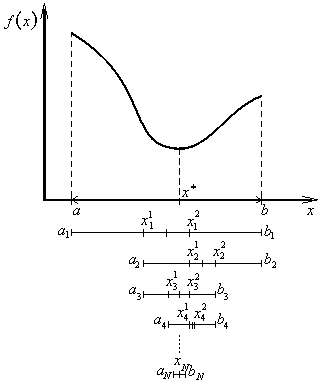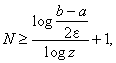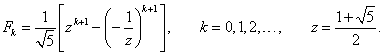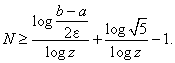2 Statická optimalizace funkcí jedné proměnné
2.2 Numerické metody jednorozměrné optimalizace
2.2.2 Přímé metody
a) Metoda kvadratické interpolace
Metoda kvadratické interpolace spočívá v aproximaci hladké unimodální účelové funkce f(x) v okolí minima kvadratickou parabolou (mnohočlenem 2. stupně). Předpokládejme, že známe hodnoty účelové funkce f(x) ve třech bodech xa < xb < xc . Označíme je fa, fb a fc. Použijeme Lagrangeův interpolační mnohočlen, který pro tento případ má tvar
|
(2.35) |
Aproximační kvadratická parabola fk(x) má ostré globální minimum ve stacionárním bodě xk, který je jediným reálným kořenem rovnice
|
(2.36) |
tj.
|
(2.37) |
Odtud dostaneme
|
(2.38) |
Pro ekvidistantní body (body stejně vzdálené od sebe) xa, xb a xc, tj. pro
|
(2.39) |
vztah (2.38) se podstatně zjednoduší
|
(2.40) |
Při řešení úloh jednorozměrné minimalizace metodou kvadratické interpolace se nejčastěji postupuje dvojím způsobem:
a)Vypočtený bod xk je dosazen ve vzorci (2.38) na místo jednoho ze tří bodů xa, xb nebo xc, a počítá se další aproximace xk+1.
b)Body xa, xb a xc jsou voleny tak, aby byly splněny podmínky (2.39) a
|
(2.41) |
Vypočtený bod xk ze vztahu (2.40) se dosadí za bod xb a další body xc a xa, jsou vybrány takovým způsobem, aby vyhovovaly podmínkám (2.39), (2.41) a počítá se další aproximace xk+1, tj.
|
(2.42) |
Rozdíl 
se na každém kroku vhodně zmenšuje.
Problém konvergence metody kvadratické interpolace je velmi složitý a závisí především na vhodné volbě bodů xa, xb a xc.
U této metody se nevypočítává počet kroků iterace a výpočet se ukončí když platí 
a výsledek se zapíše ve tvaru 
Příklad 2.7
Úlohu minimalizace z příkladu 2.1 vyřešte metodou kvadratické interpolace
Řešení:
K výpočtu použijeme vzorec (2.40), resp. (2.42).
Volíme body:
| xa = a = 0 | fa = 2 |
| xb = 0,45 |  |
| xc = 0,9 | fc = 1,82900 |
Nemůžeme volit např. body:
| xa = a = 0 | fa = 2 |
| xb = 0,5 |  |
| xc = b = 1 | fc = 2 |
protože fc - fa = 0.
Po dosazení do (2.40) dostaneme:
Volíme další body, např.:
| xa1 = 0,42 | fa1 = 1,65409 |
| xb1 = x1 = 0,52 |  |
| xc1 = 0,62 | fc1 = 1,61833 |
Ze vzorce (2.42) dostaneme:
x2 = 0,57731
Přibližné řešení:
Přesné řešení:
b) Rovnoměrná komparativní metoda
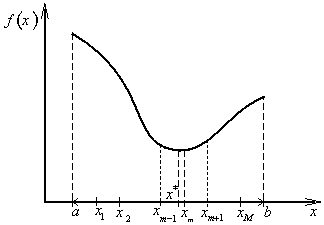
Rovnoměrná komparativní metoda (metoda rovnoměrného hledání) patří mezi nepostupné (pasivní) komparativní metody hledání minima libovolné spojité unimodální účelové funkce f(x). U této metody počáteční interval neurčitosti 
rozdělíme body
|
(2.43) |
a vyhledáme (obr. 2.9)
|
(2.44) |
|
Optimální bod x* je lokalizován v intervalu neurčitosti 
a proto lze psát
|
(2.45) |
U komparativních metod určení hodnoty účelové funkce f(x) výpočtem nebo experimentálním měřením se nazývá experiment. Efektivnost těchto metod vyjadřuje poměr délky počátečního intervalu neurčitosti k délce posledního N-tého intervalu neurčitosti při stejném počtu experimentů M , tj.
|
(2.46) |
Počet experimentů M u rovnoměrné komparativní metody při požadované přesnosti ε lze určit z nerovnosti
|
(2.47) |
ze které po úpravě dostaneme
|
(2.48) |
Shodně se vztahy (2.46) a (2.47) efektivnost rovnoměrné komparativní metody je
|
(2.49) |
c) Metoda zlatého řezu
Metoda zlatého řezu patří mezi postupné (adaptivní) komparativní metody hledání minima libovolné spojité unimodální účelové funkce f(x). Postupné komparativní metody spočívají, podobně jako Bolzanova metoda, v utvoření takové posloupnosti intervalů neurčitosti 
, která vyhovuje vztahům
|
(2.50) |
|
(2.51) |
Každý následující interval neurčitosti je podintervalem předcházejícího intervalu neurčitosti, a proto posloupnosti 
a 
konvergují:
|
(2.52) |
|
(2.53) |
Počet kroků N je dán požadovanou přesností ε, pro kterou platí vztahy:
|
(2.54) |
|
(2.55) |
kde
|
(2.56) |
Metoda zlatého řezu spočívá v rozdělení každého intervalu neurčitosti tak, aby poměr větší části k menší byl roven poměru celého děleného intervalu k větší části (obr. 2.10), tj.
|
(2.57) |
|
(2.58) |
|
Po dosazení (2.57) do (2.58) a úpravě dostaneme kvadratickou rovnici
|
(2.59) |
jejíž kladný kořen je hledaný poměr
|
(2.60) |
Platí pro něj vztahy:
|
(2.61) |
|
(2.62) |
|
(2.63) |
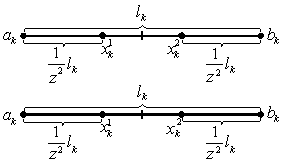
Při metodě zlatého řezu ve všech krocích (kromě prvního) interval neurčitosti obsahuje spolu s krajními body jeden vnitřní bod. Proto je třeba určit hodnotu účelové funkce f(x) pouze v jednom novém bodě umístěném symetricky k již známému bodu (obr. 2.11 a obr. 2.12).
|
|
Metodu zlatého řezu lze popsat algoritmem:
|
(2.64) |
Po N -tém kroku optimální bod x* je lokalizován v intervalu neurčitosti 
o délce
|
(2.65) |
tj.
|
(2.66) |
Potřebný počet kroků N pro určení optimálního bodu x* s přesností ε zjistíme ze vzorce
|
(2.67) |
který získáme úpravou vztahů (2.54) a (2.65). Počet experimentů M je stejný jako počet kroků N, tj.
|
(2.68) |
Efektivnost metody zlatého řezu je dána vztahem [viz (2.46) a (2.65)]
|
(2.69) |
U metody zlatého řezu se výsledek zapíše ve tvaru
|
Příklad 2.8
Úlohu minimalizace z příkladu 2.1 vyřešte metodou zlatého řezu s přesností ε = 0,01
Řešení:
Počet kroků vypočteme ze vzorce (2.67)
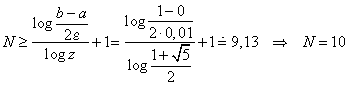
Shodně s algoritmem (2.64) pro 
lze psát:
1. krok: |
a1 = a = 0 |
|
|
|
b1 = b = 1 |
|
|||
2. krok: |
|
|
|
|
b2 = b1 = 1 |
|
|||
3. krok: |
|
|
|
|
|
|
|||
4. krok: |
|
|
|
|
|
|
|||
5. krok: |
|
|
|
|
|
|
|||
6. krok: |
|
|
|
|
|
|
|||
7. krok: |
|
|
|
|
|
|
|||
8. krok: |
|
|
|
|
|
|
|||
9. krok: |
|
|
|
|
|
|
|||
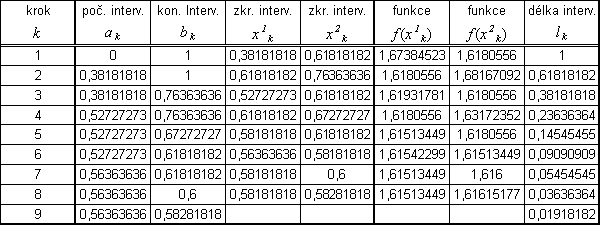
10. krok: |
|
x10 = 0,57701 |
l10 = 0,01316 |
|
|
||||
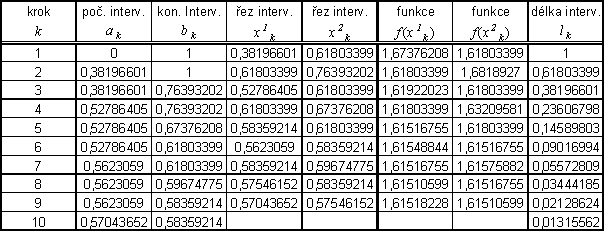
Přibližné řešení:
Zápis výsledku s ohledem na zadanou přesnost ε:
Přesné řešení:
Výsledek řešení ze souboru v Excelu (StatOpt-MetZlatRezu.xls):
d) Fibonacciova metoda
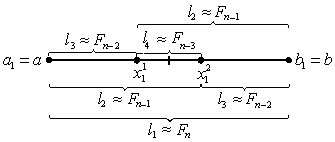
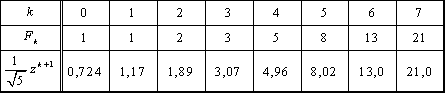
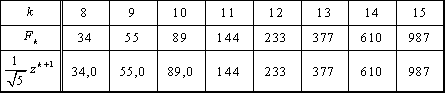
Fibonacciova (Kieferova) metoda rovněž patří mezi postupné komparativní metody, a proto pro ni platí vztahy (2.50) – (2.56). Fibonacciova metoda využívá při zkracování intervalů neurčitosti přímé úměrnosti jejich délek číslům Fibonacciovy posloupnosti (obr. 2.13), tj.
|
(2.70) |
kde čísla Fibonacciovy posloupnosti 
jsou dány vztahy
|
(2.71) |
resp.
|
(2.72) |
|
Pro veliké k lze v rovnici (2.72) výraz 
zanedbat a dostaneme přibližný vzorec pro výpočet čísel Fibonacciovy posloupnosti
|
(2.73) |
V tabulce 2.1 je uvedeno prvních 16 čísel Fibonacciovy posloupnosti a také jejich aproximace podle vztahu (2.73).
|
Tab. 2.1: Prvních 16 čísel Fibonacciovy posloupnosti
|
Fibonacciova metoda minimalizace může být popsána následujícím algoritmem:
|
(2.74) |
Malé kladné číslo γ na N-tém kroku dovoluje určit polohu optimálního bodu x* vzhledem k bodu xN-1 . Hodnotu čísla γ volíme nejméně o řád menší než je požadovaná přesnost ε. Po N-tém kroku optimální bod x* leží v intervalu 
a proto lze psát
|
(2.75) |
|
(2.76) |
Pro dosažení přesnosti ε při lokalizaci optimálního bodu x* ze vztahů (2.54) a (2.76) dostaneme
|
(2.77) |
tj. musíme najít takové číslo Fibonacciovy posloupnosti, které vyhovuje nerovnosti (2.77). Jeho index N udává počet potřebných kroků, a zároveň počet experimentů M , tzn.
|
(2.78) |
Využijeme-li v nerovnosti (2.77) aproximace (2.73), pak dostaneme přibližný vztah
|
(2.79) |
Pro efektivnost Fibonacciovy metody platí [viz vztah (2.76) a (2.78)]
|
(2.80) |
resp. přibližně
|
(2.81) |
U Fibonacciovy metody číslo N musíme znát před zahájením výpočtu.
Příklad 2.9
Úlohu minimalizace z příkladu 2.1 řešte Fibonacciovou metodou s přesností ε = 0,01
Řešení:
Počet kroků N zjistíme ze vztahu (2.77), resp. (2.79):
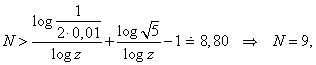
Shodně s algoritmem Fibonacciovy metody lze psát:
1. krok: |
a1 = a = 0 |
|
|
b1 = b = 1 |
|
||
2. krok: |
|
|
|
b2 = b1 = 1 |
|
||
3. krok: |
|
|
|
|
|
||
4. krok: |
|
|
|
|
|
||
5. krok: |
|
|
|
|
|
||
6. krok: |
|
|
|
|
|
||
7. krok: |
 |
 |
|
|
|
||
8. krok: |
|
|
|
|
|
||
9. krok: |
a9 = x8 = 0,56364 |
x9 = 0,57323 |
|
b9 = b8 = 0,58282 |
Přibližné řešení:
Zápis výsledku s ohledem na zadanou přesnost ε:
Přesné řešení:
Výsledek řešení ze souboru v Excelu (StatOpt-FibonacMet.xls):
