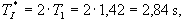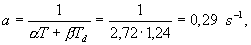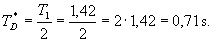Obecný tvar obrazového přenosu pro všechny tři snímače teploty je:
|
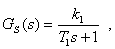 |
(1) |
|
kde pro
Pro tyto hodnoty 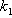 a
a  má aproximovaný průběh nejnižší hodnotu přiléhavosti
má aproximovaný průběh nejnižší hodnotu přiléhavosti 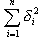
 Pro soustavu s tímto přenosem byly zvoleny, s ohledem na kvalitu regulace pouze dva typy regulátorů, a to I regulátor a PI regulátor
Pro soustavu s tímto přenosem byly zvoleny, s ohledem na kvalitu regulace pouze dva typy regulátorů, a to I regulátor a PI regulátor
Metoda standardních tvarů
Postup:
- I - regulátor
Přenos regulované soustavy (1), přenos regulátoru
|  . . | (2) | |
Přenos otevřeného regulačního obvodu (otevřené smyčky)
| 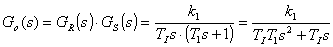 . . | (3) | |
Určení přenosu řízení
| 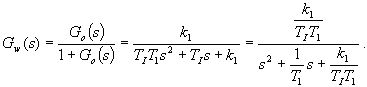 . . |
Stupeň astatismu q = 1, protože lze vytknout s ve jmenovateli  , a u
, a u 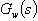 je v čitateli a jmenovateli shodný jeden člen.
je v čitateli a jmenovateli shodný jeden člen.
Určení charakteristického mnohočlenu přenosu řízení
| 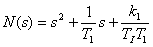 . . | (4) | |
a) Whiteleyho standardní tvary
 Pro daný stupeň astatismu q otevřeného regulačního obvodu a řád soustavy určíme z tab. 1. tvar standardního mnohočlenu. Porovnáním tohoto mnohočlenu s mnohočlenem (4) (především jejich koeficientů) určíme optimální hodnoty stavitelných parametrů regulátoru.
Pro daný stupeň astatismu q otevřeného regulačního obvodu a řád soustavy určíme z tab. 1. tvar standardního mnohočlenu. Porovnáním tohoto mnohočlenu s mnohočlenem (4) (především jejich koeficientů) určíme optimální hodnoty stavitelných parametrů regulátoru.
| Tab. 1.Standardní tvary charakteristického mnohočlenu |
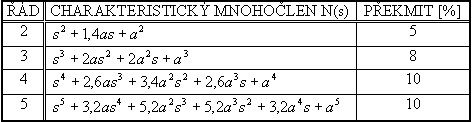 |
Dosazením rovnice (5) do rovnice (6) dostaneme optimální hodnoty integrační časové konstanty 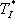 pro I regulátor
pro I regulátor
| 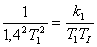 , , |
po úpravě
| 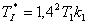 . . |
Dosazením konkrétních hodnot za 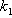 a
a  jednotlivých termistorů, dostaneme tyto hodnoty
jednotlivých termistorů, dostaneme tyto hodnoty
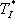
- pro termistor T2 je
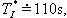
- pro termistor T3 je
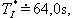
- pro termistor T4 je
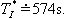
b) Standardní tvary podle kritéria ITAE
 Pro daný stupeň astatismu q = 1 je tvar charakteristického mnohočlenu 2. řádu, u této metody stejný, jako u metody Whiteleyho standardních tvarů. Získáme tedy stejné výsledky jako v bodě a.
Pro daný stupeň astatismu q = 1 je tvar charakteristického mnohočlenu 2. řádu, u této metody stejný, jako u metody Whiteleyho standardních tvarů. Získáme tedy stejné výsledky jako v bodě a.
- PI - regulátor
Přenos regulované soustavy (1), přenos regulátoru
| 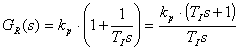 . . | (7) | |
Přenos otevřeného regulačního obvodu (otevřené smyčky)
|  . . | (8) | |
 V rovnici (8) byla provedena kompenzace časových konstant, pro zjednodušení výpočtu. Kompenzace se provádí vždy, když jde zjednodušit výpočet a znamená, že neznáme hodnotě časové konstanty regulátoru je přiřazená nejvyšší hodnota ze všech časových konstant regulované soustavy.
V rovnici (8) byla provedena kompenzace časových konstant, pro zjednodušení výpočtu. Kompenzace se provádí vždy, když jde zjednodušit výpočet a znamená, že neznáme hodnotě časové konstanty regulátoru je přiřazená nejvyšší hodnota ze všech časových konstant regulované soustavy.
Přenos řízení
|  . . |
 Řád charakteristického mnohočlenu N(s) není odpovídající pro použiti této metody. Tuto metodu lze použít, pro charakteristické mnohočleny 2. a vyššího řádu. Proto se tedy omezíme jen na splnění podmínky stability. V našem případě Stodolové podmínky, která se pro soustavu s přenosem 1. řádu stává nutnou a postačující.
Řád charakteristického mnohočlenu N(s) není odpovídající pro použiti této metody. Tuto metodu lze použít, pro charakteristické mnohočleny 2. a vyššího řádu. Proto se tedy omezíme jen na splnění podmínky stability. V našem případě Stodolové podmínky, která se pro soustavu s přenosem 1. řádu stává nutnou a postačující.
Je-li  >0,
>0, 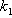 >0, pak musí být i
>0, pak musí být i 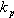 >0.
>0.
Velikost 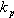 volíme s ohledem na kvalitu regulačního pochodu.
(rychlost přechodového děje × maximální velikost překmitu)
volíme s ohledem na kvalitu regulačního pochodu.
(rychlost přechodového děje × maximální velikost překmitu)
Grafická prezentace dosažených výsledků regulace teploty:
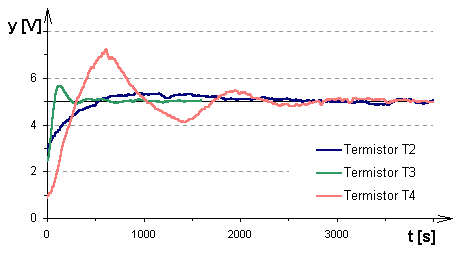
Obr. 1. Přechodová charakteristika uzavřeného regulačního obvodu s termistory T2, T3, T4 a I regulátorem
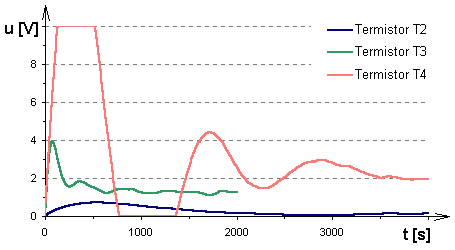
Obr. 2. Průběh akční veličiny regulačního obvodu s termistory T2, T3, T4 a I regulátorem
Číselná prezentace dosažených výsledků regulace teploty:
| Tab. 2. Zhodnocení výsledků regulace pro metodu standardních tvarů |
 |
| Pozn.: | Lepší kvality přechodového děje (snížení maximálního překmitu) u termistoru T4 nebylo dosaženo, ani několikanásobným zvýšením integrační časové konstanty 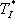 . . |
Zpět
Metoda optimálního modulu
Postup:
- I - regulátor
Přenos regulované soustavy (1), přenos regulátoru (2), přenos otevřeného regulačního obvodu (3).
Přenos řízení použijeme ve tvaru
Určení koeficientů 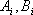
Dosazením do rovnice  vypočteme neznámy parametr
vypočteme neznámy parametr 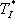 ; tzn.
Po dosazení a úpravě dostaneme
; tzn.
Po dosazení a úpravě dostaneme
| 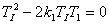 , , |
| 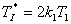 , , |
Dosazením konkrétních hodnot za 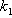 a
a  dostaneme tyto hodnoty nastavení časové konstanty
dostaneme tyto hodnoty nastavení časové konstanty 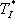 integračního regulátoru:
integračního regulátoru:
- pro termistor T2 je
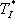
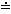 112s,
112s,
- pro termistor T3 je
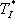
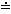 65,4s,
65,4s,
- pro termistor T4 je
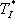
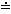 586s.
586s.
 Protože vypočtené hodnoty
Protože vypočtené hodnoty 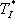 , pro daný regulátor a typ soustavy vyšly přibližně stejné jako u metody standardních tvarů, nebudou zde uvedeny grafické průběhy přechodových charakteristik a ani průběhy akčních veličin (tyto průběhy budou podobné, průběhům na obr. 1. a obr. 2).
, pro daný regulátor a typ soustavy vyšly přibližně stejné jako u metody standardních tvarů, nebudou zde uvedeny grafické průběhy přechodových charakteristik a ani průběhy akčních veličin (tyto průběhy budou podobné, průběhům na obr. 1. a obr. 2).
- PI - regulátor
Přenos regulované soustavy (1), přenos regulátoru (7), přenos otevřeného regulačního obvodu (8).
Přenos řízení použijeme ve tvaru
Určení koeficientů 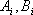 :
:
Dosazením koeficientů 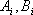 do vztahu
do vztahu  nelze vypočítat neznámy parametr
nelze vypočítat neznámy parametr 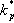 , protože
, protože
 Tato metoda není vhodná pro daný typ soustavy a PI regulátor. Seřízení regulátoru se omezí pouze na splnění podmínek stability.
Tato metoda není vhodná pro daný typ soustavy a PI regulátor. Seřízení regulátoru se omezí pouze na splnění podmínek stability.
 Aby byly splněny podmínky stability musí být parametr
Aby byly splněny podmínky stability musí být parametr  . Jeho velikost volíme s ohledem na kvalitu regulačního pochodu. Dostaneme se tedy do situace, kdy známe parametr
. Jeho velikost volíme s ohledem na kvalitu regulačního pochodu. Dostaneme se tedy do situace, kdy známe parametr 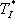 , a volíme odpovídající
, a volíme odpovídající 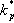 . Protože u metody inverze dynamiky řešíme stejný problém, budou i výsledky pro PI regulátor přibližně stejné, jako u této metody.
. Protože u metody inverze dynamiky řešíme stejný problém, budou i výsledky pro PI regulátor přibližně stejné, jako u této metody.
Zpět
Metoda simetrického optima
 Tato metoda se používá jen u soustav se stupněm astatismu
Tato metoda se používá jen u soustav se stupněm astatismu 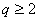 , což regulovaná soustava s termistorem nesplňuje.
, což regulovaná soustava s termistorem nesplňuje.
Zpět
Metoda inverze dynamiky
Postup:
Zjistíme, zda náhradní přenosy termistorů 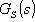 (1) jsou již v základním tvaru, a zda vyhovují podmínce pro použití této metody (tvarem přenosu
(1) jsou již v základním tvaru, a zda vyhovují podmínce pro použití této metody (tvarem přenosu 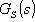 ).
).
Podle tabulky, pro výpočet stavitelných parametrů regulátoru, přiřadíme k soustavě s přenosem 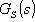 odpovídající typ regulátoru a určíme optimální hodnoty stavitelných parametrů regulátoru, pro konkrétní
odpovídající typ regulátoru a určíme optimální hodnoty stavitelných parametrů regulátoru, pro konkrétní 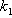 ,
,  .
.
Analogový PI regulátor 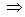 vzorkovací perioda
vzorkovací perioda  ,
,
Vypočteme optimální hodnoty integračních časových konstant dle vztahu
 | pro termistor T2 je 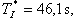 | (9) | |
 | pro termistor T3 je 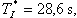 | (10) | |
 | pro termistor T4 je 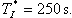 | (11) | |
- Výpočet proporcionálního zesílení regulátoru
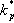
Při výpočtu zesílení regulátoru 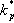 bereme v potaz velikost dopravního zpoždění. Pro
bereme v potaz velikost dopravního zpoždění. Pro 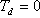 je
je 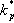 vypočteno ze vztahu
vypočteno ze vztahu
kde 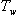 je časová konstanta, jejíž volba musí být provedena s ohledem na omezení akční veličiny, resp. maximální stavitelnou hodnotu zesílení regulátoru
je časová konstanta, jejíž volba musí být provedena s ohledem na omezení akční veličiny, resp. maximální stavitelnou hodnotu zesílení regulátoru  .
.
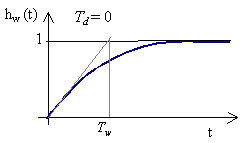
Obr. 3. Přechodová charakteristika uzavřeného regulačního obvodu bez dopravního zpoždění
Hodnota časové konstanty 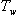 byla zvolena
byla zvolena 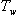 =10s, pro všechny tři snímače teploty, s ohledem na kvalitu regulačního pochodu.
=10s, pro všechny tři snímače teploty, s ohledem na kvalitu regulačního pochodu.
Grafická prezentace dosažených výsledků regulace teploty:
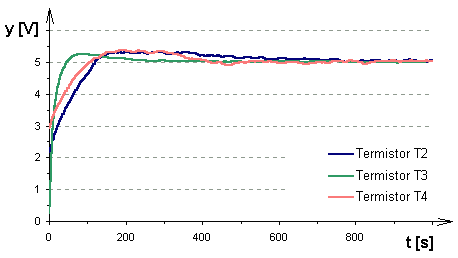
Obr. 4. Přechodová charakteristika uzavřeného regulačního obvodu s termistory T2, T3, T4 a PI regulátorem
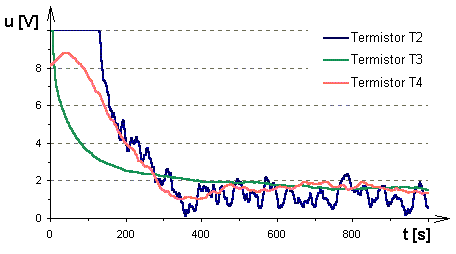
Obr. 5. Průběh akční veličiny regulačního obvodu s termistory T2, T3, T4 a PI regulátorem
Číselná prezentace dosažených výsledků regulace teploty:
| Tab. 3. Zhodnocení výsledků regulace pro metodu inverze dynamiky |
 |
Zpět
Vrtulkový průtokoměr
 Identifikací byl pro vrtulkový průtokoměr stanoven náhradní přenos ve tvaru
Identifikací byl pro vrtulkový průtokoměr stanoven náhradní přenos ve tvaru
|
 |
(1) |
|
kde 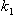 =0,91,
=0,91, 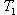 =1,42 s,
=1,42 s, 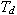 =1,24 s.
=1,24 s.
 Pro soustavu s tímto přenosem budou voleny s ohledem na kvalitu regulace pouze dva typy regulátoru, a to PI regulátor a PID regulátor.
Pro soustavu s tímto přenosem budou voleny s ohledem na kvalitu regulace pouze dva typy regulátoru, a to PI regulátor a PID regulátor.
Zieglerova - Nicholsova metoda kritického zesílení regulátoru
Postup:
Určení kritického zesílení regulátoru 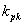 prostědnictvím simulačního programu SIPRO. Blokové schéma zapojení této simulační úlohy je na obr. 1.
prostědnictvím simulačního programu SIPRO. Blokové schéma zapojení této simulační úlohy je na obr. 1.
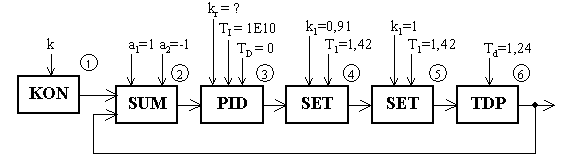
Obr. 1. Blokové schéma
| Pozn.: | Blok PID je vhodnější nahradit blokem ZES. Touto úpravou úplně eliminuje vliv integrační složky  (nastavení maximální možné hodnoty (nastavení maximální možné hodnoty  v programu SIPRO nezaručuje odstranění vlivu této časové konstanty). Blok PID byl volen proto, abychom se přiblížili reálným podmínkám. v programu SIPRO nezaručuje odstranění vlivu této časové konstanty). Blok PID byl volen proto, abychom se přiblížili reálným podmínkám. |
Postupným zvyšováním hodnoty kr (označení proporcionálního zesílení 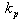 v programu SIPRO) bylo dosaženo hodnoty kr=3,47, při které obvod začal kmitat s konstantní amplitudou A, a s konstantní periodou kmitů
v programu SIPRO) bylo dosaženo hodnoty kr=3,47, při které obvod začal kmitat s konstantní amplitudou A, a s konstantní periodou kmitů 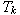 =6,05s (obr. 2).
=6,05s (obr. 2).
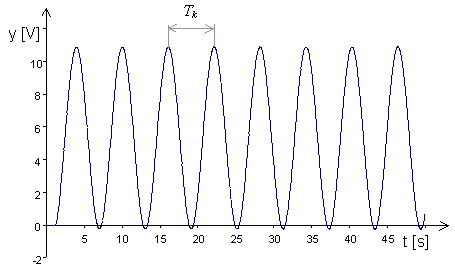
Obr. 2. Určení kritické periody kmitů 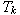
Po dosazení hodnot 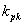 (hodnota kr při které obvod začal kmitat) a
(hodnota kr při které obvod začal kmitat) a 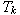 do empirických vztahů (pro danou metodu), dostaneme optimální hodnoty stavitelných parametrů PI a PID regulátoru.
do empirických vztahů (pro danou metodu), dostaneme optimální hodnoty stavitelných parametrů PI a PID regulátoru.
- PI - regulátor
PID - regulátor
Zpět
Zieglerova - Nicholsova metoda čtvrtinového tlumení
Postup:
Nastavení zesílení regulátoru  tak, aby poměr třetí amplitudy
tak, aby poměr třetí amplitudy 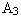 a první amplitudy
a první amplitudy 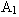 výstupní veličiny soustavy byl v poměru ¼. Pak
výstupní veličiny soustavy byl v poměru ¼. Pak 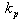
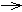
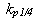 .
.
Zapojení této simulační úlohy je shodné s blokovým schématem na obr. 1.
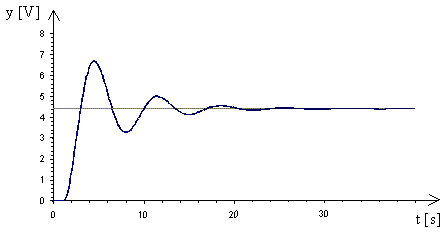
Obr. 3. Určení 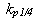 a
a  z průběhu přechodové charakteristiky vrtulkového průtokoměru
z průběhu přechodové charakteristiky vrtulkového průtokoměru
- Odečtení hodnot
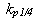 a
a  z průběhu výstupní veličiny soustavy.
z průběhu výstupní veličiny soustavy.
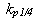 |
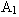 [V] [V] |
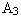 [V] [V] |
 [s] [s] |
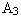 / /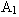 |
| 1,86 |
2,27 |
0,57 |
7,00 |
1/3,98 |
Dosazení zjištěných hodnot 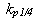 a
a  do empirických vztahů (pro danou metodu), pro výpočet jednotlivých stavitelných parametrů PI a PID regulátoru.
do empirických vztahů (pro danou metodu), pro výpočet jednotlivých stavitelných parametrů PI a PID regulátoru.
- PI - regulátor
Pro lepší kvalitu přechodového děje bylo 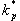 zvýšeno na hodnotu
zvýšeno na hodnotu 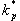 = 2 .
= 2 .
PID - regulátor
Zpět
Zieglerova - Nicholsova metoda přechodové charakteristiky
Postup:
Z grafu přechodové charakteristiky vrtulkového průtokoměru a výpočtem, ze znalosti rovnice tečny procházející inflexním bodem, byly zjištěny tyto parametry regulované soustavy:
- dopravní zpoždění
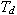 =,1s,
=,1s,
- doba průtahu
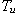 =,0,54s,
=,0,54s,
- doba náběhu
 = 4,20s,
= 4,20s,
- zesílení soustavy
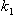 = 0,92.
= 0,92.
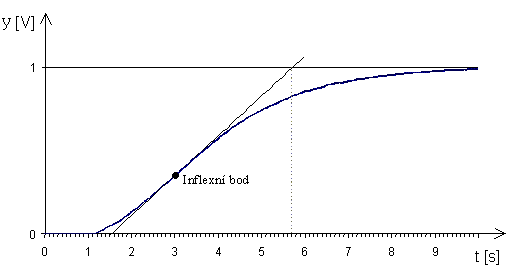
Obr. 4. Normovaná přechodová charakteristika vrtulkového průtokoměru
Dosazením těchto hodnot do empirických vztahů (pro danou metodu), dostaneme optimální hodnoty stavitelných parametrů pro jednotlivé typy regulátorů.
- PI - regulátor
PID - regulátor
Zpět
Metoda optimálního modulu
Postup:
- Dopravní zpoždění regulované soustavy
 nahradíme Padého rozvojem I řádu
nahradíme Padého rozvojem I řádu
|
 . . |
Pro snadnější výpočet zavedeme pomocnou proměnnou např. 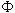
|
 . . |
Dostaneme tedy přenos soustavy ve tvaru
|
 . . |
- PI - regulátor
Přenos regulátoru
|
 . . |
Přenos otevřeného regulačního obvodu
|
 . . |
Pozn.: | Ve jmenovateli jde vytknout s 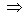 stupeň astatismu soustavy q = 1, lze tedy tuto metodu použít. stupeň astatismu soustavy q = 1, lze tedy tuto metodu použít. |
Přenos řízení
po roznásobení
|
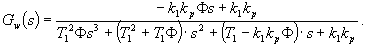 . . | (2) | |
 Vyjádření součinitelů
Vyjádření součinitelů 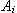 a
a 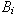 z přenosu
z přenosu 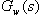 (2):
(2):
Pro výpočet optimálních hodnot stavitelných parametrů regulátoru postačí určení jen těchto čtyř součinitelů (zejména 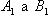 ).
).
Dosazením součinitelů 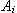 a
a 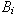 do vztahu
do vztahu  optimální hodnoty stavitelných parametrů regulátoru:
optimální hodnoty stavitelných parametrů regulátoru:
po úpravě
Optimální hodnota 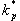 tedy je
tedy je
Hodnoty stavitelných parametrů PI regulátoru po dosazení konkrétních hodnot za 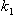 ,
, 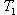 a
a 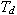 tedy jsou:
tedy jsou:
Proporcionální zesílení regulátoru bylo v zájmu lepší kvality regulačního pochodu sníženo na hodnotu 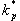 = 0,15.
= 0,15.
Optimální hodnota integrační časové konstanty
- PID - regulátor
Přenos regulátoru
Přenos otevřeného regulačního obvodu
Pozn.: | Ve jmenovateli jde vytknout s 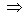 stupeň astatismu soustavy q = 1, lze tedy tuto metodu použít. stupeň astatismu soustavy q = 1, lze tedy tuto metodu použít. |
Přenos řízení
Vyjádření součinitelů 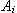 a
a 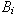 z přenosu
z přenosu 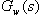 (3):
(3):
Pro výpočet optimálních hodnot stavitelných parametrů regulátoru postačí určení jen těchto čtyř součinitelů (zejména 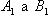 ).
).
Dosazením součinitelů 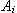 a
a 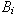 do vztahu
do vztahu  optimální hodnoty stavitelných parametrů regulátoru:
optimální hodnoty stavitelných parametrů regulátoru:
po úpravě
Optimální hodnota 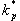 tedy je
tedy je
| |
 . . |
Hodnoty stavitelných parametrů PID regulátoru po dosazení za 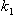 ,
, 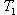 a
a 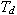 jsou:
jsou:
Zpět
Metoda standardních tvarů
Postup:
 Pro proporcionální soustavu se setrvačnosti 2. řádu s dopravním zpožděním použijeme aproximaci
Pro proporcionální soustavu se setrvačnosti 2. řádu s dopravním zpožděním použijeme aproximaci
abychom dostali 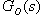 v požadovaném (standardním) tvaru pro použití této metody. Při použití této aproximace však dostaneme velmi nepřesný výsledek, který neumožňuje použití této metody.
v požadovaném (standardním) tvaru pro použití této metody. Při použití této aproximace však dostaneme velmi nepřesný výsledek, který neumožňuje použití této metody.
 Závěr: Nepoužívat aproximaci dopravního zpoždění ve tvaru
Závěr: Nepoužívat aproximaci dopravního zpoždění ve tvaru
Metoda inverze dynamiky
Regulovanou soustavě s přenosem (1), byl přiřazen vhodný PID analogový regulátor. Požadavek na seřízení regulátoru byl takový, aby relativní překmit κ při skokové změně polohy žádané veličiny byl nulový.
Postup:
 Určení optimálních hodnot stavitelných parametrů analogového regulátoru ze vztahů:
Určení optimálních hodnot stavitelných parametrů analogového regulátoru ze vztahů:
zpět
Prezentace dosažených výsledků regulace průtoku vzduchu PI regulátorem: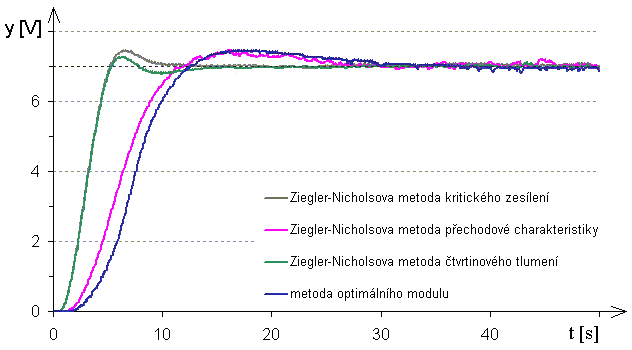
Obr. 5. Přechodové charakteristiky uzavřeného regulačního obvodu, pro danou metodu syntézy a PI regulátor
Prezentace dosažených výsledků regulace průtoku vzduchu PID regulátorem:
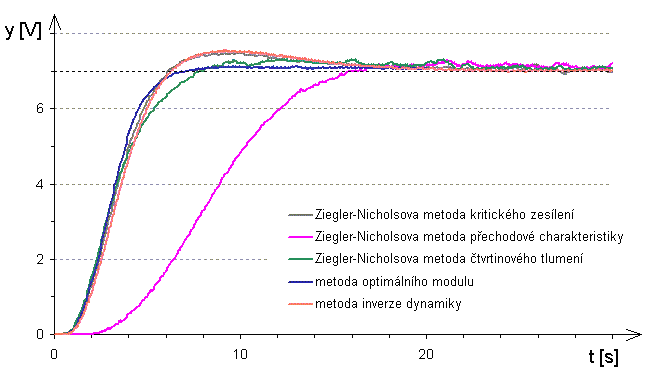
Obr. 6. Přechodové charakteristiky uzavřeného regulačního obvodu, pro danou metodu syntézy a PID regulátor
| Tab.4. Zhodnocení výsledků regulace průtoku vzduchu |
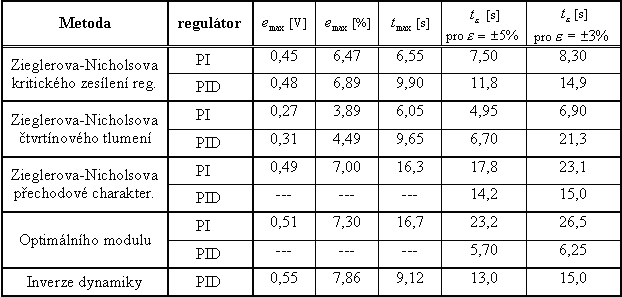
|
Zpět
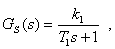
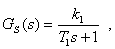
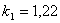 ,
, 
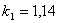 ,
,
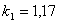 ,
, 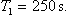
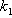 a
a  má aproximovaný průběh nejnižší hodnotu přiléhavosti
má aproximovaný průběh nejnižší hodnotu přiléhavosti 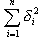
 Pro soustavu s tímto přenosem byly zvoleny, s ohledem na kvalitu regulace pouze dva typy regulátorů, a to I regulátor a PI regulátor
Pro soustavu s tímto přenosem byly zvoleny, s ohledem na kvalitu regulace pouze dva typy regulátorů, a to I regulátor a PI regulátor
 .
.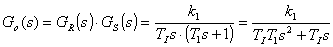 .
.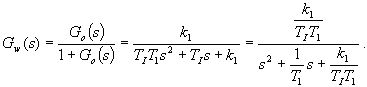 .
. , a u
, a u 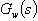 je v čitateli a jmenovateli shodný jeden člen.
je v čitateli a jmenovateli shodný jeden člen.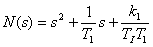 .
. Pro daný stupeň astatismu q otevřeného regulačního obvodu a řád soustavy určíme z tab. 1. tvar standardního mnohočlenu. Porovnáním tohoto mnohočlenu s mnohočlenem (4) (především jejich koeficientů) určíme optimální hodnoty stavitelných parametrů regulátoru.
Pro daný stupeň astatismu q otevřeného regulačního obvodu a řád soustavy určíme z tab. 1. tvar standardního mnohočlenu. Porovnáním tohoto mnohočlenu s mnohočlenem (4) (především jejich koeficientů) určíme optimální hodnoty stavitelných parametrů regulátoru.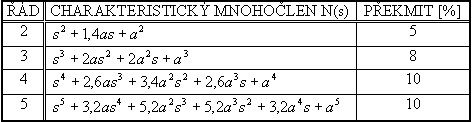
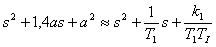
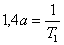
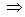
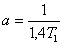
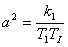
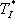 pro I regulátor
pro I regulátor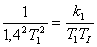 ,
,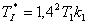 .
.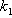 a
a  jednotlivých termistorů, dostaneme tyto hodnoty
jednotlivých termistorů, dostaneme tyto hodnoty
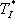
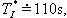
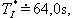
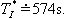
 Pro daný stupeň astatismu q = 1 je tvar charakteristického mnohočlenu 2. řádu, u této metody stejný, jako u metody Whiteleyho standardních tvarů. Získáme tedy stejné výsledky jako v bodě a.
Pro daný stupeň astatismu q = 1 je tvar charakteristického mnohočlenu 2. řádu, u této metody stejný, jako u metody Whiteleyho standardních tvarů. Získáme tedy stejné výsledky jako v bodě a.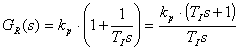 .
. .
. V rovnici (8) byla provedena kompenzace časových konstant, pro zjednodušení výpočtu. Kompenzace se provádí vždy, když jde zjednodušit výpočet a znamená, že neznáme hodnotě časové konstanty regulátoru je přiřazená nejvyšší hodnota ze všech časových konstant regulované soustavy.
V rovnici (8) byla provedena kompenzace časových konstant, pro zjednodušení výpočtu. Kompenzace se provádí vždy, když jde zjednodušit výpočet a znamená, že neznáme hodnotě časové konstanty regulátoru je přiřazená nejvyšší hodnota ze všech časových konstant regulované soustavy. .
. Řád charakteristického mnohočlenu N(s) není odpovídající pro použiti této metody. Tuto metodu lze použít, pro charakteristické mnohočleny 2. a vyššího řádu. Proto se tedy omezíme jen na splnění podmínky stability. V našem případě Stodolové podmínky, která se pro soustavu s přenosem 1. řádu stává nutnou a postačující.
Řád charakteristického mnohočlenu N(s) není odpovídající pro použiti této metody. Tuto metodu lze použít, pro charakteristické mnohočleny 2. a vyššího řádu. Proto se tedy omezíme jen na splnění podmínky stability. V našem případě Stodolové podmínky, která se pro soustavu s přenosem 1. řádu stává nutnou a postačující.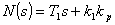
 >0,
>0, 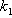 >0, pak musí být i
>0, pak musí být i 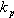 >0.
>0.
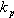 volíme s ohledem na kvalitu regulačního pochodu.
(rychlost přechodového děje × maximální velikost překmitu)
volíme s ohledem na kvalitu regulačního pochodu.
(rychlost přechodového děje × maximální velikost překmitu)



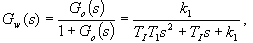
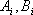

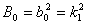
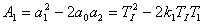
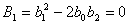
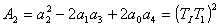
 vypočteme neznámy parametr
vypočteme neznámy parametr 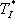 ; tzn.
; tzn.

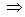
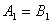
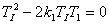 ,
,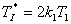 ,
,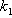 a
a  dostaneme tyto hodnoty nastavení časové konstanty
dostaneme tyto hodnoty nastavení časové konstanty 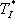 integračního regulátoru:
integračního regulátoru: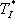
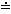 112s,
112s,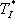
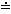 65,4s,
65,4s,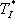
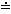 586s.
586s. Protože vypočtené hodnoty
Protože vypočtené hodnoty 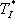 , pro daný regulátor a typ soustavy vyšly přibližně stejné jako u metody standardních tvarů, nebudou zde uvedeny grafické průběhy přechodových charakteristik a ani průběhy akčních veličin (tyto průběhy budou podobné, průběhům na obr. 1. a obr. 2).
, pro daný regulátor a typ soustavy vyšly přibližně stejné jako u metody standardních tvarů, nebudou zde uvedeny grafické průběhy přechodových charakteristik a ani průběhy akčních veličin (tyto průběhy budou podobné, průběhům na obr. 1. a obr. 2).
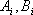 :
:
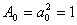
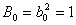
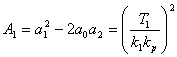
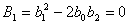
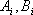 do vztahu
do vztahu  nelze vypočítat neznámy parametr
nelze vypočítat neznámy parametr 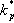 , protože
, protože
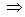
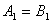
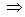
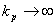
 Tato metoda není vhodná pro daný typ soustavy a PI regulátor. Seřízení regulátoru se omezí pouze na splnění podmínek stability.
Tato metoda není vhodná pro daný typ soustavy a PI regulátor. Seřízení regulátoru se omezí pouze na splnění podmínek stability. Aby byly splněny podmínky stability musí být parametr
Aby byly splněny podmínky stability musí být parametr  . Jeho velikost volíme s ohledem na kvalitu regulačního pochodu. Dostaneme se tedy do situace, kdy známe parametr
. Jeho velikost volíme s ohledem na kvalitu regulačního pochodu. Dostaneme se tedy do situace, kdy známe parametr 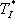 , a volíme odpovídající
, a volíme odpovídající 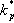 . Protože u metody inverze dynamiky řešíme stejný problém, budou i výsledky pro PI regulátor přibližně stejné, jako u této metody.
. Protože u metody inverze dynamiky řešíme stejný problém, budou i výsledky pro PI regulátor přibližně stejné, jako u této metody. Tato metoda se používá jen u soustav se stupněm astatismu
Tato metoda se používá jen u soustav se stupněm astatismu 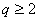 , což regulovaná soustava s termistorem nesplňuje.
, což regulovaná soustava s termistorem nesplňuje. 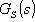 (1) jsou již v základním tvaru, a zda vyhovují podmínce pro použití této metody (tvarem přenosu
(1) jsou již v základním tvaru, a zda vyhovují podmínce pro použití této metody (tvarem přenosu 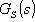 ).
).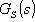 odpovídající typ regulátoru a určíme optimální hodnoty stavitelných parametrů regulátoru, pro konkrétní
odpovídající typ regulátoru a určíme optimální hodnoty stavitelných parametrů regulátoru, pro konkrétní 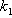 ,
,  .
.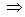 vzorkovací perioda
vzorkovací perioda  ,
, 

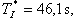

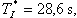

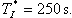
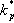
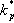 bereme v potaz velikost dopravního zpoždění. Pro
bereme v potaz velikost dopravního zpoždění. Pro 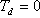 je
je 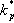 vypočteno ze vztahu
vypočteno ze vztahu 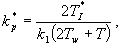
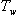 je časová konstanta, jejíž volba musí být provedena s ohledem na omezení akční veličiny, resp. maximální stavitelnou hodnotu zesílení regulátoru
je časová konstanta, jejíž volba musí být provedena s ohledem na omezení akční veličiny, resp. maximální stavitelnou hodnotu zesílení regulátoru  .
.
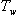 byla zvolena
byla zvolena 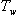 =10s, pro všechny tři snímače teploty, s ohledem na kvalitu regulačního pochodu.
=10s, pro všechny tři snímače teploty, s ohledem na kvalitu regulačního pochodu.
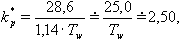
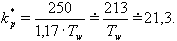



 Identifikací byl pro vrtulkový průtokoměr stanoven náhradní přenos ve tvaru
Identifikací byl pro vrtulkový průtokoměr stanoven náhradní přenos ve tvaru

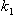 =0,91,
=0,91, 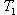 =1,42 s,
=1,42 s, 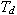 =1,24 s.
=1,24 s.
 Pro soustavu s tímto přenosem budou voleny s ohledem na kvalitu regulace pouze dva typy regulátoru, a to PI regulátor a PID regulátor.
Pro soustavu s tímto přenosem budou voleny s ohledem na kvalitu regulace pouze dva typy regulátoru, a to PI regulátor a PID regulátor. prostědnictvím simulačního programu SIPRO. Blokové schéma zapojení této simulační úlohy je na obr. 1.
prostědnictvím simulačního programu SIPRO. Blokové schéma zapojení této simulační úlohy je na obr. 1.
 (nastavení maximální možné hodnoty
(nastavení maximální možné hodnoty  v programu SIPRO nezaručuje odstranění vlivu této časové konstanty). Blok PID byl volen proto, abychom se přiblížili reálným podmínkám.
v programu SIPRO nezaručuje odstranění vlivu této časové konstanty). Blok PID byl volen proto, abychom se přiblížili reálným podmínkám. v programu SIPRO) bylo dosaženo hodnoty kr=3,47, při které obvod začal kmitat s konstantní amplitudou A, a s konstantní periodou kmitů
v programu SIPRO) bylo dosaženo hodnoty kr=3,47, při které obvod začal kmitat s konstantní amplitudou A, a s konstantní periodou kmitů 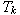 =6,05s (obr. 2).
=6,05s (obr. 2).
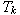
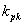 (hodnota kr při které obvod začal kmitat) a
(hodnota kr při které obvod začal kmitat) a 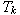 do empirických vztahů (pro danou metodu), dostaneme optimální hodnoty stavitelných parametrů PI a PID regulátoru.
do empirických vztahů (pro danou metodu), dostaneme optimální hodnoty stavitelných parametrů PI a PID regulátoru.

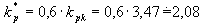

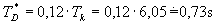
 tak, aby poměr třetí amplitudy
tak, aby poměr třetí amplitudy 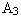 a první amplitudy
a první amplitudy 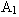 výstupní veličiny soustavy byl v poměru ¼. Pak
výstupní veličiny soustavy byl v poměru ¼. Pak 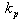
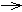
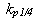 .
.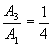

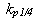 a
a  z průběhu přechodové charakteristiky vrtulkového průtokoměru
z průběhu přechodové charakteristiky vrtulkového průtokoměru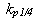 a
a  z průběhu výstupní veličiny soustavy.
z průběhu výstupní veličiny soustavy.
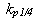
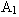 [V]
[V]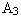 [V]
[V] [s]
[s]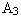 /
/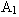
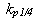 a
a  do empirických vztahů (pro danou metodu), pro výpočet jednotlivých stavitelných parametrů PI a PID regulátoru.
do empirických vztahů (pro danou metodu), pro výpočet jednotlivých stavitelných parametrů PI a PID regulátoru.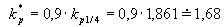

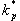 zvýšeno na hodnotu
zvýšeno na hodnotu 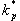 = 2 .
= 2 .

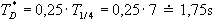
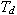 =,1s,
=,1s,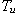 =,0,54s,
=,0,54s, = 4,20s,
= 4,20s,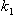 = 0,92.
= 0,92.
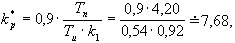
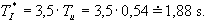
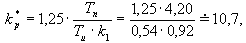
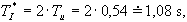
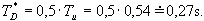
 nahradíme Padého rozvojem I řádu
nahradíme Padého rozvojem I řádu .
.
 .
. .
. .
. .
. stupeň astatismu soustavy q = 1, lze tedy tuto metodu použít.
stupeň astatismu soustavy q = 1, lze tedy tuto metodu použít.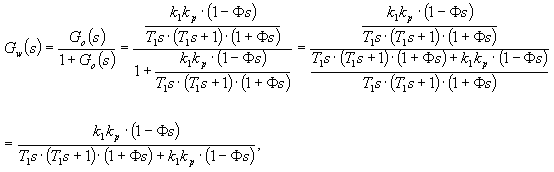
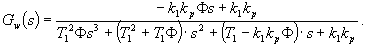 .
. Vyjádření součinitelů
Vyjádření součinitelů 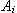 a
a 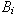 z přenosu
z přenosu 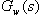 (2):
(2):



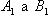 ).
).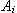 a
a 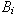 do vztahu
do vztahu  optimální hodnoty stavitelných parametrů regulátoru:
optimální hodnoty stavitelných parametrů regulátoru: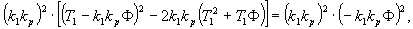

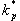 tedy je
tedy je

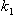 ,
, 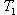 a
a 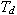 tedy jsou:
tedy jsou: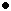
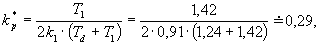
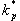 = 0,15.
= 0,15.
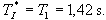

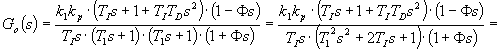

 .
.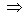 stupeň astatismu soustavy q = 1, lze tedy tuto metodu použít.
stupeň astatismu soustavy q = 1, lze tedy tuto metodu použít.

 .
.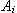 a
a 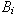 z přenosu
z přenosu 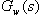 (3):
(3):


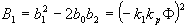
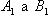 ).
).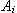 a
a 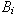 do vztahu
do vztahu  optimální hodnoty stavitelných parametrů regulátoru:
optimální hodnoty stavitelných parametrů regulátoru: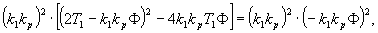

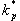 tedy je
tedy je
 .
.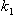 ,
, 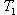 a
a 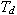 jsou:
jsou: 

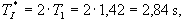
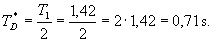
 Pro proporcionální soustavu se setrvačnosti 2. řádu s dopravním zpožděním použijeme aproximaci
Pro proporcionální soustavu se setrvačnosti 2. řádu s dopravním zpožděním použijeme aproximaci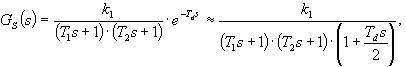
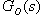 v požadovaném (standardním) tvaru pro použití této metody. Při použití této aproximace však dostaneme velmi nepřesný výsledek, který neumožňuje použití této metody.
v požadovaném (standardním) tvaru pro použití této metody. Při použití této aproximace však dostaneme velmi nepřesný výsledek, který neumožňuje použití této metody. Závěr: Nepoužívat aproximaci dopravního zpoždění ve tvaru
Závěr: Nepoužívat aproximaci dopravního zpoždění ve tvaru
 Určení optimálních hodnot stavitelných parametrů analogového regulátoru ze vztahů:
Určení optimálních hodnot stavitelných parametrů analogového regulátoru ze vztahů: