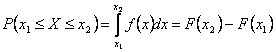Náhodná veličina
Náhodná veličina X je proměnná, jejíž hodnota x je jednoznačně určena výsledkem náhodného pokusu. Charakteristickým rysem náhodné veličiny je, že při opakování náhodného pokusu dochází vlivem náhodných činitelů k měnlivosti hodnot. Nemůžeme před provedením pokusu určit, jaké hodnoty veličina nabude [Škrášek, J., Tichý, Z., 1990], [Vítečková, M.].
Tabulka 2.2: Dělení náhodné veličiny
Nabývá libovolných hodnot z určitého intervalu (např. odečet z měřicího přístroje) |
Nabývá konečný počet hodnot z intervalu (např. kostka, ruleta) |
|
Distribuční funkce |
|
|
|
|
|
|
|
|
|
|
|
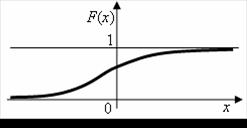
Distribuční funkce je funkce neklesající. |
|
|
|
|
|
Obr. 2.6 Hladká funkce |
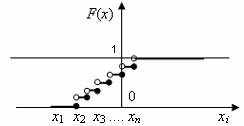
Obr. 2.7 Schodovitá funkce |
|
Hustota pravděpodobnosti |
Frekvenční funkce |
|
|
|
|
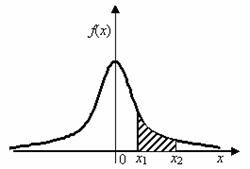
Obr. 2.8 Hustota pravděpodobnosti
|
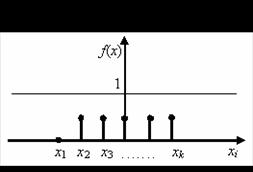
Obr. 2.9 Frekvenční funkce
|
Číselné charakteristiky náhodných veličin
Číselné charakteristiky popisují některé základní rysy náhodných veličin, jako například obecné a centrální momenty [Škrášek, J., Tichý, Z., 1990].
Tabulka 2.3 Charakteristiky náhodných veličin
|
Spojitá náhodná
veličina |
Diskrétní
náhodná veličina |
|
Obecný moment náhodné veličiny s-tého řádu |
|
|
|
|
|
Obecný moment náhodné veličiny prvního řádu (střední hodnota) |
|
|
|
|
|
Centrální moment s-tého řádu |
|
|
|
|
|
Obecný zápis centrálního momentu:
ms[X] = E[(X - E[X])s] |
|
|
Důkaz: (pro diskrétní NV)
|
|
|
|
|
|
|
|
|
Směrodatná odchylka (standardní, střední kvadratická odchylka)
|
|
|
Vlastnosti m a s2 (platí pro spojité i diskrétní náhodné veličiny) C - konstanta X, Y - náhodné veličiny (platí pro spojité i diskrétní) m - střední hodnota s 2 - rozptyl náhodné veličiny |
|
|
|
|
Zde jsou příklady na procvičení probrané látky. Náhodná veličina.