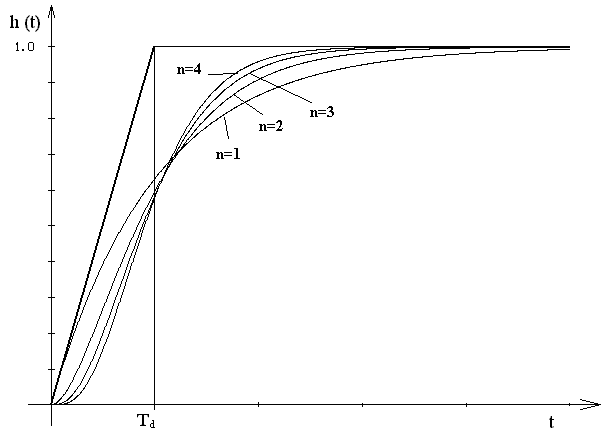
obrázek 18 – Aproximace dopravního zpoždění dle vztahu 18
V regulačních obvodech se často vyskytuje člen dopravního zpoždění, který představuje exponenciální výraz e-Td s. Tento člen dopravního zpoždění je buď vlastností regulované soustavy nebo se vyskytne v případě použití číslicového regulátoru. Tím máme vlastnosti regulované soustavy popsány vztahem, který obsahuje exponenciální funkci a pokud chceme použít metody syntézy regulačních obvodů pro lineární regulační obvody neobsahující dopravní zpoždění, musíme toto dopravní zpoždění aproximovat. Dále jsou uvedeny používané aproximace.

obrázek 18 – Aproximace dopravního zpoždění dle vztahu 18
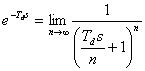 . . |
(17) |
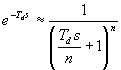 . . |
(18) |
V praxi se používá n = 1, n = 2. Čím větší je n, tím je aproximace přesnější. Tato aproximace se vyznačuje jednoduchostí, avšak málo se používá, neboť člen s minimální fází (člen s dopravním zpožděním) se nahrazuje členem s minimální fází.
Aproximace Taylorovým rozvojem:
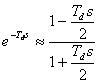 . . |
(19) |
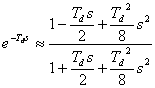 . . |
(20) |
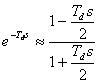 . . |
(21) |
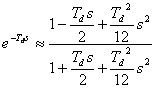 . . |
(21a) |
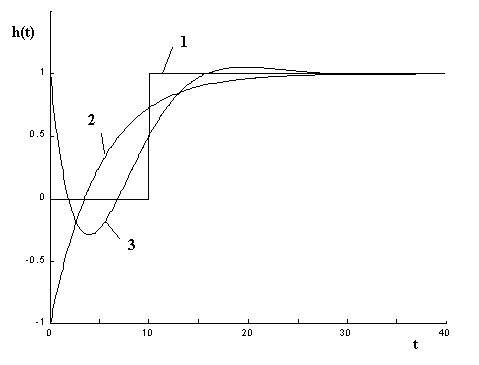
1 – dopravní zpoždění e-Td s, 2 – aproximace Padého rozvojem a Taylorovým rozvojem I. řádu, 3 – aproximace Taylorovým rozvojem II. řádu
obrázek 19 – Aproximace dopravního zpoždění Padého a Taylorovým rozvojem