Syntézou regulačního obvodu rozumíme stanovení struktury a parametrů regulačního obvodu, tak aby byly splněny požadavky, kladené na regulační pochod (dosažení cíle řízení).
Syntézou regulačního obvodu rozumíme stanovení struktury a parametrů regulačního obvodu, tak aby byly splněny požadavky, kladené na regulační pochod (dosažení cíle řízení). Syntézou regulačního obvodu rozumíme stanovení struktury a parametrů regulačního obvodu, tak aby byly splněny požadavky, kladené na regulační pochod (dosažení cíle řízení).
Syntézou regulačního obvodu rozumíme stanovení struktury a parametrů regulačního obvodu, tak aby byly splněny požadavky, kladené na regulační pochod (dosažení cíle řízení).
| stabilní regulační obvod, |
| minimální doba regulace | 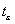 | obr. 1, |
| požadovaný relativní překmit | 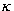 | obr. 1, |
| minimalizace vlivu poruchových veličin, |
| přesné sledování žádané hodnoty regulovanou veličinou, |
| nulová trvalá regulační odchylka, |
| ROBUSTNOST regulačního obvodu na změnu parametrů soustavy. |
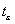 - - |
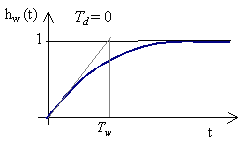
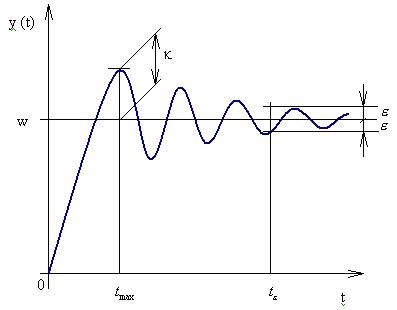
Doba regulace. Doba, za kterou se průběh regulačního pochodu dostane trvale do pásma ± 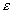 od žádané hodnoty od žádané hodnoty |
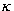 - - |
Maximální překmit. Zpravidla první amplituda křivky regulačního pochodu |
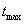 - - |
Doba, kdy regulovaná veličina dosáhla maximální hodnoty |
 - - |
Přesnost regulace - pásmo regulace (většinou ± 3% nebo ± 5%) |
 Volba struktury (typu) regulátoru je určená především vlastnostmi soustavy, kterou chceme regulovat. Přehled typu regulátoru k dané soustavě je uveden v tabulce 1.
Volba struktury (typu) regulátoru je určená především vlastnostmi soustavy, kterou chceme regulovat. Přehled typu regulátoru k dané soustavě je uveden v tabulce 1.
| Typ regulátoru | Hodí se k regulaci soustav |
| I | proporcionálních se setrvačností 1. řádu, s malou časovou konstantou, bez dopravního zpoždění, při malých a pomalých změnách zatížení, |
| P | proporcionálních i integračních se setrvačností 1. řádu, se střední časovou konstantou, popř. s malým dopravním zpožděním, při malých změnách zatížení; (zanechává trvalou regulační odchylku), |
| PI | proporcionálních i integračních se setrvačností vyššího řádu s libovolnými časovými konstantami, s velkým dopravním zpožděním, při velkých a pomalých změnách zatížení, |
| PD | proporcionálních i integračních se setrvačností vyššího řádu se středními časovými konstantami, s velkým dopravním zpožděním při malých změnách zatížení; (zanechává trvalou regulační odchylku), |
| PID | proporcionálních i integračních se setrvačností vyššího řádu s libovolnými časovými konstantami i s delším dopravním zpožděním, při velkých a rychlých změnách zatížení, |
| Dvoupolohový | proporcionálních se setrvačností 1. řádu, s velkou časovou konstantou, bez dopravního zpoždění, při malých změnách zatížení. |
Zieglerova - Nicholsova metoda kritického zesílení
Zieglerova - Nicholsova metoda čtvrtinového tlumení
Zieglerova - Nicholsova metoda přechodové charakteristiky
Seřízení regulátoru metodou standardních tvarů
 Metoda podle J.G. Zieglera a N.B. Nicholse je metoda experimentální a umožňuje seřízení regulátoru přímo za provozních podmínek.
Metoda podle J.G. Zieglera a N.B. Nicholse je metoda experimentální a umožňuje seřízení regulátoru přímo za provozních podmínek.
 Princip metody spočívá v přivedení regulační obvodu do tzv. kritického stavu, tj. na kmitavou mez stability, přičemž regulátor pracuje pouze s proporcionální složkou (tohoto stavu regulátoru je dosaženo dosazením do rovnice 1). Integrační a derivační složka regulátoru je vyřazena nastavením integrační časové konstanty na co možná nejvyšší hodnotu
Princip metody spočívá v přivedení regulační obvodu do tzv. kritického stavu, tj. na kmitavou mez stability, přičemž regulátor pracuje pouze s proporcionální složkou (tohoto stavu regulátoru je dosaženo dosazením do rovnice 1). Integrační a derivační složka regulátoru je vyřazena nastavením integrační časové konstanty na co možná nejvyšší hodnotu 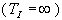 a derivační časové konstanty na nulovou hodnotu
a derivační časové konstanty na nulovou hodnotu 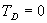 .
.
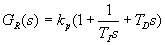 |
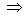 |
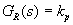 |
(1) |
Experimentální seřízení regulátoru aplikací metody
Postup: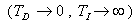 .
. Postupným opatrným zvyšováním zesílení regulátoru  , přivedeme obvod na mez stability (do kritického stavu). V tomto okamžiku začne obvod kmitat s konstantní amplitudou
, přivedeme obvod na mez stability (do kritického stavu). V tomto okamžiku začne obvod kmitat s konstantní amplitudou 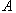 , a s konstantní periodou kmitů
, a s konstantní periodou kmitů 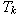 .
.
Hodnota zesílení regulátoru 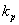 , při které regulační obvod dosáhne meze stability, je označena jako kritické zesílení
, při které regulační obvod dosáhne meze stability, je označena jako kritické zesílení 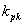 . Periodu kmitů, s kterou obvod na mezi stability kmitá, se pak nazývá kritickou periodou
. Periodu kmitů, s kterou obvod na mezi stability kmitá, se pak nazývá kritickou periodou 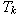 (obr. 2).
(obr. 2).
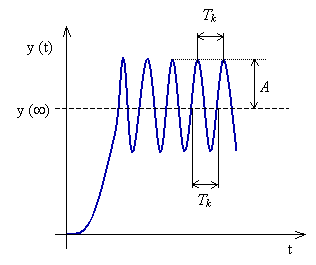
Po dosazení zjištěných hodnot kpk a Tk do empirických vztahů pro daný typ regulátoru v tab. 2, vypočteme optimální hodnoty stavitelných parametrů ( ,
, 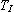 a
a 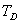 ) příslušného regulátoru.
) příslušného regulátoru.
| Tab. 2. Optimální hodnoty stavitelných parametrů regulátoru |
| Typ regulátoru | 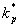
|
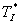
|
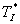
|
| P | 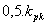
|
----- | ----- |
| PI |
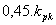
|
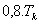
|
----- |
| PD |
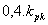
|
----- |
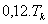
|
| PID | 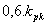
|
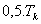
|
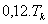
|
 Seřízení ryze integračního regulátoru provedeme postupným zmenšováním integrační časové konstanty
Seřízení ryze integračního regulátoru provedeme postupným zmenšováním integrační časové konstanty 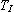 , tak dlouho, až v obvodu vzniknou netlumené harmonické kmity. Tím dosáhneme kmitavé meze stability a integrační časová konstanta pro daný okamžik se stává kritickou
, tak dlouho, až v obvodu vzniknou netlumené harmonické kmity. Tím dosáhneme kmitavé meze stability a integrační časová konstanta pro daný okamžik se stává kritickou 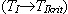 .
.
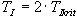 |
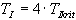 |
| Pozn: | Zesílení regulátoru zvětšujeme opatrně, protože náhlé a velké zesílení by mohlo vést k destrukci seřizované soustavy ( |
 Tato modifikace Zieglerovy-Nicholsovy metody jako jediná nemá analytické řešení a jedná se o čistě experimentální metodu.
Používá se v případě, kdy regulační obvod nelze přivést na kmitavou mez stability, nebo tam, kde by mohlo na kmitavé mezi stability dojít k poškození samotné regulované soustavy.
Tato modifikace Zieglerovy-Nicholsovy metody jako jediná nemá analytické řešení a jedná se o čistě experimentální metodu.
Používá se v případě, kdy regulační obvod nelze přivést na kmitavou mez stability, nebo tam, kde by mohlo na kmitavé mezi stability dojít k poškození samotné regulované soustavy.
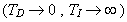
Zvyšování zesílení regulátoru  tak dlouho, až poměr třetí amplitudy
tak dlouho, až poměr třetí amplitudy 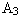 a první amplitudy
a první amplitudy 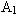 bude ¼, tzn.
bude ¼, tzn.
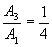 |
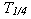 . Zesílení regulátoru
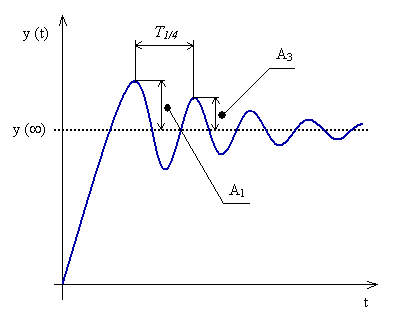
. Zesílení regulátoru  , při kterém k tomu došlo, nazveme čtvrtinové zesílení regulátoru
, při kterém k tomu došlo, nazveme čtvrtinové zesílení regulátoru 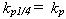 .
.
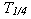
| Tab. 3. Optimální hodnoty stavitelných parametrů regulátoru |
| Typ regulátoru | 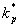
|
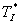
|
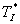
|
| P | 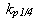
|
----- | ----- |
| PI |
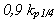
|
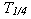
|
----- |
| PID | 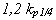
|
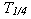
|
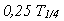
|
 U této metody syntézy soustavy vycházíme ze znalosti průběhu přechodové charakteristiky. Používáme ji pro soustavy s aperiodickým průběhem odezvy (bez překmitu).
U této metody syntézy soustavy vycházíme ze znalosti průběhu přechodové charakteristiky. Používáme ji pro soustavy s aperiodickým průběhem odezvy (bez překmitu).
Bod, kde tečna protne časovou osu, určí dobu průtahu 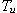 (její konec) a dobu náběhu
(její konec) a dobu náběhu 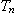 (její začátek), viz. obr. 4. Doba náběhu je určena průsečíkem tečny s časovou osou a s pořadnicí ustáleného stavu.
(její začátek), viz. obr. 4. Doba náběhu je určena průsečíkem tečny s časovou osou a s pořadnicí ustáleného stavu.
| Pozn: | Není-li od počátku přechodového děje patrná odezva systému, označíme tuto dobu jako dopravní zpoždění |

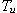 a doby náběhu
a doby náběhu 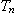
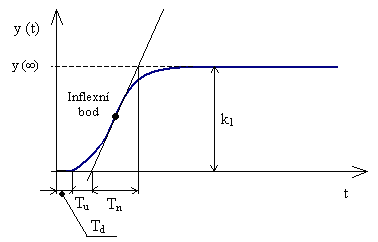
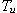 a doby náběhu
a doby náběhu 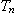 u soustav s dopravním zpožděním
u soustav s dopravním zpožděním 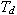
Odečtené hodnoty doby průtahu 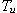 , doby náběhu
, doby náběhu 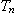 a zesílení soustavy
a zesílení soustavy 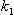 dosadíme do tab.4 a určíme optimální hodnoty stavitelných parametrů pro daný typ regulátoru.
dosadíme do tab.4 a určíme optimální hodnoty stavitelných parametrů pro daný typ regulátoru.
| Tab. 4. Optimální hodnoty stavitelných parametrů regulátoru |
| Typ regulátoru | 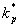
|
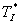
|
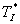
|
| P | 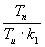
|
----- | ----- |
| PI |
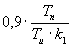
|
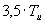
|
----- |
| PD |
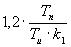
|
----- |
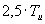
|
| PID | 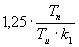
|
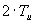
|
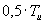
|
 Tato metoda vychází z určitých vzorových typů přenosů uzavřeného regulačního obvodu
Tato metoda vychází z určitých vzorových typů přenosů uzavřeného regulačního obvodu 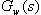 , o kterých víme, že dávají vyhovující kvalitu regulačního pochodu. Podle těchto přenosovů upravujeme seřízením parametrů regulátorů hodnoty koeficientů přenosu pro danou regulovanou soustavu tak, aby se koeficienty této konkrétní funkce a funkce vzorové navzájem rovnaly.
, o kterých víme, že dávají vyhovující kvalitu regulačního pochodu. Podle těchto přenosovů upravujeme seřízením parametrů regulátorů hodnoty koeficientů přenosu pro danou regulovanou soustavu tak, aby se koeficienty této konkrétní funkce a funkce vzorové navzájem rovnaly.
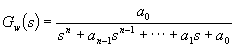
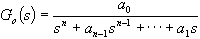
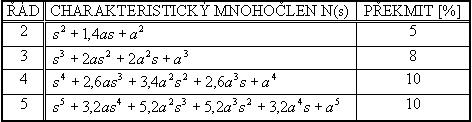
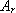 =1
=1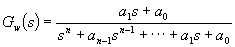
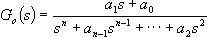
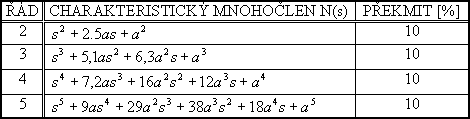
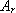 =1,1
=1,1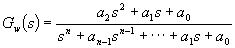
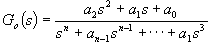
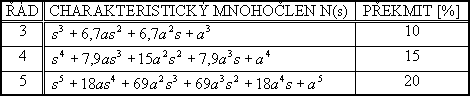
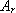 =1,4
=1,4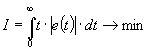 |
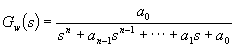
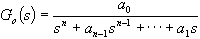
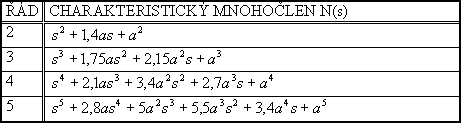
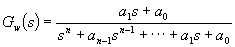
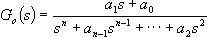
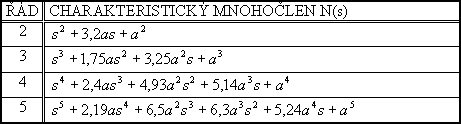
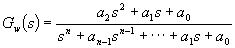
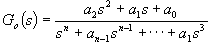
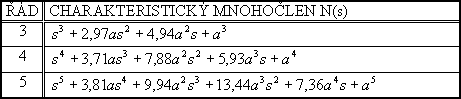
K dané regulované soustavě navrhneme vhodný typ regulátoru, např. dle tabulky 1.
Určíme obrazový přenos otevřeného regulačního obvodu 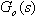 (2) a stupeň astatismu tohoto přenosu, a je-li to možné, provedeme při výpočtu
(2) a stupeň astatismu tohoto přenosu, a je-li to možné, provedeme při výpočtu 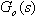 kompenzaci časových konstant. Dalším krokem bude výpočet přenosu řízení dané soustavy
kompenzaci časových konstant. Dalším krokem bude výpočet přenosu řízení dané soustavy 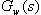 (3). Nebude-li shodný se standardním tvarem pro dané q, budeme muset od této metody seřízení regulátoru upustit.
(3). Nebude-li shodný se standardním tvarem pro dané q, budeme muset od této metody seřízení regulátoru upustit.
Je-li splněn bod 2, pak charakteristický mnohočlen uzavřeného regulačního obvodu položíme roven standardnímu mnohočlenu z tab. 5-10 (dle stupně astatismu q a použité metody).
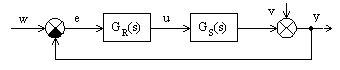
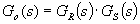 | (2) | ||
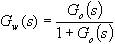 | (3) |
 Kritérium vychází ze skutečnosti, že maximum na křivce
Kritérium vychází ze skutečnosti, že maximum na křivce 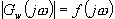 signalizuje rezonanční jev, tj. náchylnost uzavřeného regulačního obvodu k málo tlumeným kmitům.
signalizuje rezonanční jev, tj. náchylnost uzavřeného regulačního obvodu k málo tlumeným kmitům.
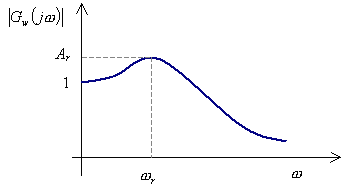
 Z obr. 7 je patrné rezonanční zvětšení modulu -
Z obr. 7 je patrné rezonanční zvětšení modulu - 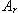 . Mezi rezonančním zvětšením modulu a maximálním překmitem regulačního pochodu je souvislost. Čím větší je rezonanční zvětšení, tím větší je i maximální překmit. Kritérium je odvozeno z podmínky minima kvadratické plochy.
. Mezi rezonančním zvětšením modulu a maximálním překmitem regulačního pochodu je souvislost. Čím větší je rezonanční zvětšení, tím větší je i maximální překmit. Kritérium je odvozeno z podmínky minima kvadratické plochy.
 Má-li být splněn cíl řízení
Má-li být splněn cíl řízení 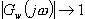 , pak musí být také splněno
, pak musí být také splněno 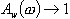 . Pak optimální přechodový děj nastane tehdy, bude-li se amplituda
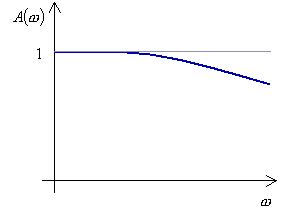
. Pak optimální přechodový děj nastane tehdy, bude-li se amplituda 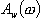 co možná v největším rozsahu frekvenci blížit jedné a bude monotónně klesat bez rezonance obr. 8.
co možná v největším rozsahu frekvenci blížit jedné a bude monotónně klesat bez rezonance obr. 8.
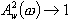 .
.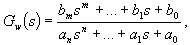 |
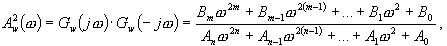 |
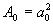 | 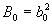 | |
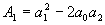 | 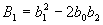 | |
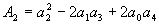 | 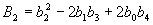 | |
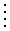 | 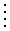 | |
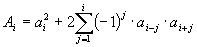 | 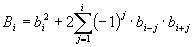 | |
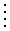 | 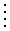 | |
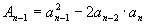 | 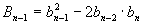 | |
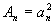 | 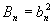 |
 Teoretickým cílem řízení je, aby se
Teoretickým cílem řízení je, aby se 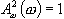 , tedy
, tedy 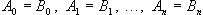 . Tohoto však nemůžeme dosáhnout, protože neexistuje reálný systém, pro který platí n = m (slabá podmínka fyzikální realizovatelnosti). Pro všechny reálné objekty platí n > m (silná podmínka fyzikální realizovatelnosti) a tedy platí, že
. Tohoto však nemůžeme dosáhnout, protože neexistuje reálný systém, pro který platí n = m (slabá podmínka fyzikální realizovatelnosti). Pro všechny reálné objekty platí n > m (silná podmínka fyzikální realizovatelnosti) a tedy platí, že
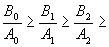 ..... ..... 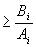 . . |
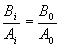 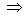 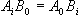 kde i = 1, 2, … kde i = 1, 2, … |
Získáme tak soustavu podmínek, jejichž jejíchž řešením dostaneme hodnoty stavitelných parametrů regulátoru pro optimální seřízení regulátoru.
Při výpočtu přenosu řízení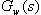 použijeme, je-li to možné, kompenzaci časových konstant.
použijeme, je-li to možné, kompenzaci časových konstant.Kritérium optimálního modulu v sobě nezahrnuje podmínky stability, proto je nutné splnění podmínek stability prověřit, a před samotnou aplikací této metody na reálný objekt i simulačně ověřit. Používá se pro systémy se stupněm astatismu q < 2.
V praxi je výhodné použít již vypočtených hodnot stavitelných parametrů pro vybrané charakteristické soustavy. Používá se pro systémy se stupněm astatismu q
Používá se pro systémy se stupněm astatismu q 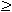 2 a vychází z metody optimálního modulu.
Její odlišnost od metody optimálního modulu spočívá v tom, že jednotlivé koeficienty
2 a vychází z metody optimálního modulu.
Její odlišnost od metody optimálního modulu spočívá v tom, že jednotlivé koeficienty 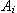 pokládáme rovny nule.
pokládáme rovny nule.
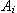 = 0 = 0 |
 Tato metoda se používá pro seřizování standardních typů konvenčních regulátorů pro regulované soustavy, a to především pro soustavy s dopravním zpožděním. Metoda inverze dynamiky zachovává jednoduchost Zieglerovy-Nicholsovy metody, ale je přesnější, univerzálnější a umožňuje jednotný přístup k seřízení analogových i číslicových regulátorů.
Tato metoda se používá pro seřizování standardních typů konvenčních regulátorů pro regulované soustavy, a to především pro soustavy s dopravním zpožděním. Metoda inverze dynamiky zachovává jednoduchost Zieglerovy-Nicholsovy metody, ale je přesnější, univerzálnější a umožňuje jednotný přístup k seřízení analogových i číslicových regulátorů.
 Seřízení regulátoru metodou inverze dynamiky vyžaduje, aby obrazový přenos regulované soustavy byl ve standardním tvaru:
Seřízení regulátoru metodou inverze dynamiky vyžaduje, aby obrazový přenos regulované soustavy byl ve standardním tvaru:
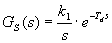 | |
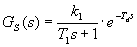 | |
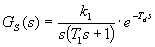 | |
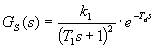 | |
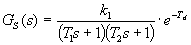 | |
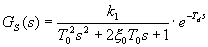 | |
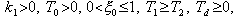 |
 - časová konstanta kmitavé regulované soustavy 2. řádu,
- časová konstanta kmitavé regulované soustavy 2. řádu,  - koeficient poměrného tlumení kmitavé regulované soustavy 2.řádu .
- koeficient poměrného tlumení kmitavé regulované soustavy 2.řádu .
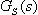 .
.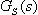 je ve tvaru vhodném pro použití této metody.
je ve tvaru vhodném pro použití této metody.K dané soustavě s přenosem 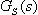 přiřadíme odpovídající typ regulátoru podle tab. 11 a vypočteme jednotlivé stavitelné parametry regulátoru.
přiřadíme odpovídající typ regulátoru podle tab. 11 a vypočteme jednotlivé stavitelné parametry regulátoru.
| Tab. 11. Vztahy pro výpočet stavitelných parametrů regulátoru |

| V tab. 11 je: | T - vzorkovací perioda,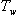 - časová konstanta uzavřeného regulačního obvodu bez dopravního zpoždění, - časová konstanta uzavřeného regulačního obvodu bez dopravního zpoždění,a - experimentálně zpřesněné zesílení otevřeného regulačního obvodu s dopravním zpožděním a číslicovým regulátorem pro požadovaný překmit. |
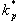 u soustav s dopravním zpožděním
u soustav s dopravním zpožděním 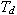 , a jeho hodnota je závislá na zvoleném relativním překmitu
, a jeho hodnota je závislá na zvoleném relativním překmitu  uzavřeného regulačního obvodu.
uzavřeného regulačního obvodu. | (4) |
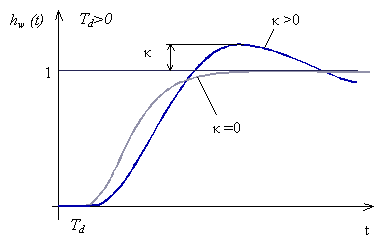
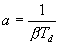 | (5) |
 .
.
 |
0 | 0,05 | 0,10 | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | 0,40 | 0,45 | 0,50 |
| α | 1,282 | 0,984 | 0,884 | 0,832 | 0,763 | 0,697 | 0,669 | 0,640 | 0,618 | 0,599 | 0,577 |
| β | 2,718 | 1,944 | 1,720 | 1,561 | 1,437 | 1,337 | 1,248 | 1,172 | 1,104 | 1,045 | 0,992 |
 U soustav bez dopravního zpoždění
U soustav bez dopravního zpoždění 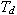 = 0, vyjde aperiodický průběh odezvy uzavřeného regulačního obvodu, tedy bez relativního překmitu
= 0, vyjde aperiodický průběh odezvy uzavřeného regulačního obvodu, tedy bez relativního překmitu  . Dynamika přechodového děje je pak závislá na hodnotě zvolené časové konstanty
. Dynamika přechodového děje je pak závislá na hodnotě zvolené časové konstanty 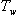 (obr.10).
(obr.10).
 Volba časové konstanty
Volba časové konstanty 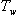 musí být provedena s ohledem na omezení akční veličiny, tedy s ohledem na maximální nastavitelnou hodnotu zesílení regulátoru
musí být provedena s ohledem na omezení akční veličiny, tedy s ohledem na maximální nastavitelnou hodnotu zesílení regulátoru 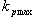 .
.