U regulačního obvodu s regulovanou soustavou - nadrž s odčerpáváním provedeme jeho analýzu s dvoupolohovým regulátorem a analogovým regulátorem typu P, viz obr. 3.1
Matematický model
V souladu s výsledky dříve řešenéhoho příkladu matematický model regulované soustavy nádrže s odčerpáváním v oblasti komplexní proměnné má tvar
[viz vztah (22) a obr. 3.1]
![]()
a) Dvoupolohový regulátor
Budeme předpokládat nejjednodušší dvoupolohový regulátor, který je realizován solenoidovým ventilem. Jeho činnost lze popsat vztahy (obr. 3.2)
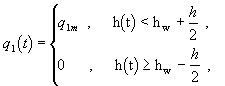
| kde hw | je | požadovaná výška hladiny [m], |
| h | - | šířka hystereze dvoupolohového regulátoru [m], |
| q1m | - | maximální přítok [m3s-1]. |
![]()
![]()
b) Analogový regulátor typu P
Analogový regulátor proporcionálního typu je nejjednodušší spojitý regulátor, který
v našem případě můžeme v oblasti komplexní proměnné popsat rovnicemi (obr. 3.3)
![]()
![]()
kde E(s) je obraz regulační odchylky,
kR - zesílení regulátoru [m2s-1].
Pro regulační obvod na obr. 3.3 platí
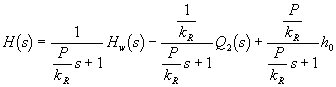
![]()
resp.
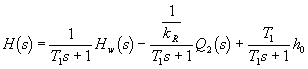
![]()
kde T1 je časová konstanta [s].
Jako poruchovou veličinu budeme uvažovat odčerpávané množství q2(t).
Ze vztahu (3.6a) je zřejmé, že počáteční výška h0 má vliv pouze na přechodný proces, protože platí (obr.3.4).
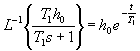
Z tohoto důvodu se vliv počteční výšky h0 (počátení podmínky) často při analýze
a syntéze regulačních obvodů neuvažuje.
Protože úkolem regulace je udržovat výšku hladiny h(t) na požadované konstantní výšce hw , pro ustálený stav platí
![]()
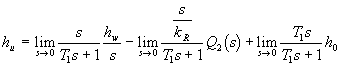
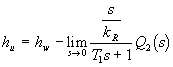
Ze vztahu (3.9) vyplývá, že při použití proporcionálního regulátoru (regulátoru typu P) v regulačním obvodě zůstane trvalá regulační odchylka, jejiž velikost závisí na odčerpávaném množství q2(t), tj.
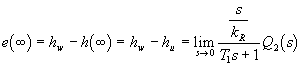
Pro skokovou změnu polohy
![]()
dostaneme
![]()
Trvalá regulační odchylka (3.12) bude tím menší, čím větší bude zesílení regulátoru kR.
Zesílení regulátotoru kR má vliv na dynamiku celého regulačního obvodu, viz vztah (3.6b).
Simulační model
Pro simulaci využijeme část schématu z příkladu nádrže s odčerpáváním (obr. 3.7).
a) Dvoupolohový regulátor {soubor NAD_O_RD.SIP}
Simulační schéma na obr. 3.7 doplníme o zapojení s dvoupolohovým regulátorem
na obr.3.5.
Pro simulaci byly zvoleny tyto hodnoty:
t12 = 80 s; q2u = 0,002 m3s-1;
P = 0,5 m; h0 = 0,2 m; hmax = 0,3 m;
q1m = 0,003 m3s-1
; h = 0,02 m; hw = 0,27 m.
Na základě výsledků simulace, viz obr. 3.6 lze učinit tyto závěry:
b) Analogový regulátor typu P{soubor NAD_O_RP.SIP}
Simulační schéma na obr. 3.7 doplníme o zapojení s analogovým regulátorem
na obr.3.8.
Pro simulaci byly zvoleny tyto hodnoty:
t1 = 30 s; t2 = 80 s; q2u = 0,002 m3s-1;
P = 0,5 m; h0 = 0,2 m; hmax= 0,3 m;
q1m = 0,003 m3s-1; hw = 0,27 m; kR = 0,1m s-1.
Na základě obr. 3.9 můžeme zhodnotit analogovou regulaci:
Na základě linearizovaného modelu nádrže s volným odtokem z příkladu 2.3 navrhneme analogový regulátor typu P, který zajistí požadovanou výšku
hladiny hw [m] s relativní trvalou regulační odchylkou k = 0,05 (5![]() ). Výsledek srovnáme na základě číslicové simulace s původním nelineárním modelem.
). Výsledek srovnáme na základě číslicové simulace s původním nelineárním modelem.
Matematický model
Linearizovaný model nádrže s volným odtokem jako regulovaná soustava má tvar [viz příklad 2.3, vztahy (2.15),(2.22) a (2.26)]
![]()
![]()
![]()
![]()
Je zřejmé, že tento linearizovaný model platí pro pracovní bod (3.13d) a pro malé odchylky od něho. Regulační obvod s analogovým regulátorem typu P je na obr. 3.11.
Přenos analogového regulátoru typu P je velmi jednoduchý
![]()
kde kR je zesílení regulátoru [m2s-1].
Na základě blokového schématu regulačního obvodu můžeme snadno určit přenos řízení
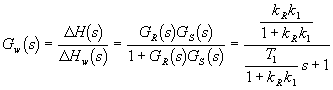
a obraz regulační odchylky
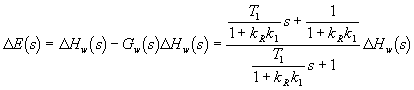
Na základě věty o koncové hodnotě můžeme ze vztahu (3.17) určit trvalou regulační odchylku pro ![]() hw(t) =
hw(t) =
![]() hw = konst.
hw = konst.
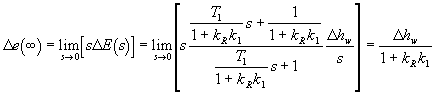
Vidíme, že trvalá regulační odchylka ![]() e(
e(![]() ) bude tím menší, čím větší bude
zesílení regulátoru kR. Ke stejnému závěru jsme mohli dojít na základě přenosu řízení (3.15), protože v jeho čitateli vystupuje
výraz
) bude tím menší, čím větší bude
zesílení regulátoru kR. Ke stejnému závěru jsme mohli dojít na základě přenosu řízení (3.15), protože v jeho čitateli vystupuje
výraz
![]()
který je vždy menší než 1, tzn.
![]()
Určíme nyní zesílení regulátoru kR, které zajistí relativní trvalou regulační odchylku
k = 0,05 (5![]() ). Na základě vztahu (3.17) lze psát
). Na základě vztahu (3.17) lze psát
![]()
![]()
resp. s využitím vztahu (3.13c) dostaneme
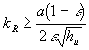
Protože reálná regulovaná soustava je nelineární, musíme použít ostrou nerovnost a pro k = 0,05 obdržíme
![]()
Simulační model
Blokové schéma regulačních obvodů s nelineární a linearizovanou soustavou
je na obr. 3.12, ze kterého je zřejmé, že s výhodou můžeme použít většinu
bloků ze simulačního schématu na obr 2.15. Výsledné simulační schéma je
na obr. 3.13 , {soubor NAD_P_R.SIP}.
Simulační výsledky na obr. 3.14 ukazují na oprávněnost použití při návrhu
regulačního obvodu linearizace ve zvoleném pracovním bodě, určeném výškou hladiny hu. Na základě vztahu (3.22) je zřejmé, že pro
![]() h > 0 pro zjištění K = 0,05 (
h > 0 pro zjištění K = 0,05 (![]() ) musíme zesílení regulátoru u regulačního obvodu s nelineární regulovanou soustavou zvýšit.
) musíme zesílení regulátoru u regulačního obvodu s nelineární regulovanou soustavou zvýšit.
Zaměníme-li regulátory typu P za regulátory typu I v obou regulačních obvodech, trvalé regulační odchylky budou nulové.
Pro simulaci byly zvoleny tyto hodnoty:
t1 = 10 s; ![]() hw =
hw = ![]() 0,1 m;
P = 0,5 m; hu = 0,2 m; kR = 0,2 m s-1; a = 0,0044
0,1 m;
P = 0,5 m; hu = 0,2 m; kR = 0,2 m s-1; a = 0,0044 ![]() .
.
Manipulátor je tvořen otočným sloupem 3, který je otáčen elektromotorem 1 přes čelní ozubené soukolí (viz obr. 3.15).Sloup unáší výsuvné rameno 4, které je vysouváno a zasouváno elektromotorem 2 přes ozubený hřeben a pastorek. Výsuvné rameno je možno považovat za tenkou homogenní tyč. Všechny součásti manipulátoru považujeme za dokonale tuhé.
Provedeme analytickou identifikaci manipulátoru a pro získaný matematický model navrhneme vhodný regulátor pro regulaci vysunutí ramena r(t) za předpokladu, že sloup se neotáčí, tzn. ![]() (t)=konst. Je použit stejnosměrný motor s konstantním buzením řízený:
(t)=konst. Je použit stejnosměrný motor s konstantním buzením řízený:
a) proudem kotvy i(t).
b) napětím kotvy u(t).
Indukčnost kotvy neuvažujeme.
Matematický model
a) Stejnosměrný motor řízený proudem kotvy
Matematický model stejnosměrného motoru s konstantním buzením řízený proudem kotvy má tvar [viz kapitola 2.5, vztahy (2.40), (2.42)]
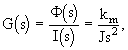
kde ![]() (s) je obraz úhlu natočení motoru [rad], I(s) - obraz proudu kotvy A, J - celkový moment setrvačnosti [kg.m2], km - konstanta motoru [N.m.A-1], s - komplexní proměnná v Laplaceově transformaci.
(s) je obraz úhlu natočení motoru [rad], I(s) - obraz proudu kotvy A, J - celkový moment setrvačnosti [kg.m2], km - konstanta motoru [N.m.A-1], s - komplexní proměnná v Laplaceově transformaci.
b) Stejnosměrný motor řízený napětím kotvy
Matematický model stejnosměrného motoru s konstantním buzením řízený napětím má tvar [viz kapitola 2.5, vztahy (2.46), (2.48), (2.50), (2.51)]
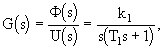
kde ![]() (s) je obraz úhlu natočení motoru [rad], U(s) - obraz napětí kotvy [V], T1 - časová konstanta [s], k1 - koeficient přenosu motoru [rad.s-1.V-1].
(s) je obraz úhlu natočení motoru [rad], U(s) - obraz napětí kotvy [V], T1 - časová konstanta [s], k1 - koeficient přenosu motoru [rad.s-1.V-1].
c) Identifikace pohybu manipulátoru
Budeme řídit vysunutí ramene manipulátoru r(t) za předpokladu, že sloup se neotáčí, tzn. ![]() (t)=konst. Celkový moment setrvačnosti J je vlastně redukovaný moment na hřídel motoru, který vysunuje a zasunuje rameno. Redukovaný moment setrvačnosti určíme na základě rovnosti kinetických energií, která je dána vztahem
(t)=konst. Celkový moment setrvačnosti J je vlastně redukovaný moment na hřídel motoru, který vysunuje a zasunuje rameno. Redukovaný moment setrvačnosti určíme na základě rovnosti kinetických energií, která je dána vztahem
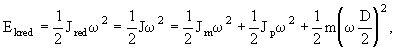
kde ![]() je úhlová rychlost [rad.s-1], Jm
- moment setrvačnosti motoru [kg.m2], Jp
- moment setrvačnosti pastorku [kg.m2], m - hmotnost výsuvného
ramena [kg], D - průměr roztečné kružnice ramena [m].
je úhlová rychlost [rad.s-1], Jm
- moment setrvačnosti motoru [kg.m2], Jp
- moment setrvačnosti pastorku [kg.m2], m - hmotnost výsuvného
ramena [kg], D - průměr roztečné kružnice ramena [m].
Z toho plyne
![]()
Vysouvání a zasouvání ramena manipulátoru je prováděno elektromotorem přes ozubený hřeben a pastorek, proto vztah mezi natočením hřídele motoru a vysunutím ramena manipulátoru má tvar
![]()
Po použití Laplaceovy transformace dostaneme vztah
![]()
kde R(s) je obraz vysunutí ramena, ![]() (s) - obraz úhlu natočení výstupního hřídele motoru.
(s) - obraz úhlu natočení výstupního hřídele motoru.
Regulace posuvu ramena manipulátoru
a) Stejnosměrný motor s konstantním buzením řízený proudem kotvy
Přenos regulované soustavy (motor + manipulátor, viz obr. 3.16)
![]()
Stupeń astatismu regulované soustavy je q = 2, tzn. jedná se o integrační soustavu druhého řádu bez setrvačnosti. Volíme proporcionální-derivační regulátor (PD regulátor), který v našem případě můžeme v oblasti komplexní proměnné popsat rovnicemi
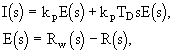
kde E(s) je obraz regulační odchylky, Rw(s) - obraz požadovaného vysunutí ramena, R(s) - obraz skutečnoho vysunutí ramena, kp - zesílení regulátoru [A.rad-1], TD - derivační časová konstanta [s].
Hodnoty parametrů regulátoru kp a TD jsme určili na základě metody symetrického optima.
b) Stejnosměrný motor s konstantním buzením řízený napětím kotvy
Přenos regulované soustavy (motor + manipulátor, viz obr. 3.18)
![]()
Stupeń astatismu regulované soustavy je q = 1, tzn. jedná se o integrační soustavu se setrvačností prvního řádu. Volíme proporcionální regulátor (P regulátor), který v našem případě můžeme v oblasti komplexní proměnné popsat rovnicemi
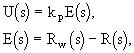
kde E(s) je obraz regulační odchylky, Rw(s) - obraz požadovaného vysunutí ramena, R(s) - obraz skutečnoho vysunutí ramena, kp - zesílení regulátoru [V.rad-1].
Hodnotu parametru regulátoru kp jsme určili pomocí metody optimálního modulu.
Simulační ověření
a)Motor řízený proudem kotvy {soubor RAPROUD.SIP}
Blokové schéma regulačního obvodu je na obr. 3.18 a jemu odpovídající simulační model je na obr. 3.20.
Popis modelu:
| blok1 | - | realizuje žádanou veličinu ve tvaru skokové změny z hodnoty 0 na hodnotu Rw, která nastane v čase t = 0, |
| blok2 | - | sumátor, na jeho výstupu je rozdíl mezi žádaným a skutečným vysunutím ramena manipulátoru, |
| bloky 3,4,5 | - | regulátor s omezením na minimální a maximální hodnotu proudu, |
| bloky 6,7,8 | - | regulovaná soustava, kde
|
| bloky 9,10 | - | přičtení počáteční hodnoty vysunutí ramena manipulátoru. |
Výsledky číslicové simulace jsou na obr. 3.21. Cílem řízení bylo dosažení
požadovaného vysunutí ramena manipulátoru. Vidíme, že po počátečních překmitech se rameno dostalo do požadované hodnoty 0,7m v čase t=19,55s.
Maximální překmit k je 39![]() tzn., že rameno se vysunulo do polohy 0,9792m.
tzn., že rameno se vysunulo do polohy 0,9792m.
Pro simulaci byly zvoleny tyto hodnoty:
m=96kg, l=1m, D=0,07m, JP=0,0006kg.m2, Jm=0,00046kg.m2,
r0=0,3m, km=0,473N.m.A-1, Imax=13,6A, k=2,1142, T=0,2585s, kp=500, TD=0,175s.
b)Motor řízený napětím kotvy{soubor RANAPETI.SIP}
Blokové schéma regulačního obvodu je na obr. 3.19 a jemu odpovídající
simulační model je na obr. 3.22.
Popis modelu:
| blok1 | - | realizuje žádanou veličinu ve tvaru skokové změny z hodnoty 0 na hodnotu Rw, která nastane v čase t = 0, |
| blok 2 | - | sumátor, na jeho výstupu je rozdíl mezi žádaným a skutečným vysunutí ramena manipulátoru, |
| bloky 3,4 | - | regulátor s omezením na maximální hodnotu napětí, |
| bloky 5, 6, 7 | - | regulovaná soustava, |
| bloky 8, 9 | - | přičtení počáteční hodnoty vysunutí ramena manipulátoru. |
Výsledky číslicové simulace jsou na obr. 3.23. Cílem řízení bylo dosažení
požadovaného vysunutí ramena manipulátoru. Vidíme, že po počátečním překmitu se rameno dostalo do požadované hodnoty 0,7m v čase t=4,6s.
Maximální překmit vysunutí ramena k je 5,5![]() tzn., že rameno se vysune na hodnotu 0,739m.
tzn., že rameno se vysune na hodnotu 0,739m.
Pro simulaci byly zvoleny tyto hodnoty:
m=96kg, l=1m, D=0,07m, JP=0,0006kg.m2, Jm=0,00046kg.m2,
r0=0,3m, km=0,473N.m.A-1, km=0,473N.m.A-1,
Umax=149V, k=2,1142, T=0,372s, kp=24,4.
Manipulátor je tvořen otočným sloupem 3, který je otáčen elektromotorem 1 přes čelní ozubené soukolí (viz obr. 3.24).Sloup unáší výsuvné rameno 4, které je vysouváno a zasouváno elektromotorem 2 přes ozubený hřeben a pastorek. Výsuvné rameno je možno považovat za tenkou homogenní tyč. Všechny součásti manipulátoru považujeme za dokonale tuhé.
Provedeme analytickou identifikaci manipulátoru a pro získaný matematický model navrhneme vhodný regulátor pro regulaci natočení sloupu
![]() (t) za ředpokladu, že rameno je ve střední poloze a nepohybuje se, tzn. r(t)=0.5l=konst. Je použit stejnosměrný motor s konstantním buzením řízený:
(t) za ředpokladu, že rameno je ve střední poloze a nepohybuje se, tzn. r(t)=0.5l=konst. Je použit stejnosměrný motor s konstantním buzením řízený:
a) proudem kotvy i(t)
b) napětím kotvy u(t)
Indukčnost kotvy neuvažujeme.
Matematický model
a) Stejnosměrný motor řízený proudem kotvy
Matematický model stejnosměrného motoru s konstantním buzením řízený proudem kotvy má tvar [viz kapitola 2.5, vztahy (2.40),(2.42)]
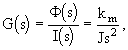
kde ![]() (s) je obraz úhlu natočení motoru [rad], I(s) - obraz proudu kotvy A, J - celkový moment setrvačnosti [kg.m2], km - konstanta motoru [N.m.A-1], s - komplexní proměnná v Laplaceově ransformaci.
(s) je obraz úhlu natočení motoru [rad], I(s) - obraz proudu kotvy A, J - celkový moment setrvačnosti [kg.m2], km - konstanta motoru [N.m.A-1], s - komplexní proměnná v Laplaceově ransformaci.
b) Stejnosměrný motor řízený napětí kotvy
Matematický model stejnosměrného motoru s onstantním buzením řízený napětím má tvar [viz kapitola 2.5, vztahy (2.48), (2.50), (2.51)]
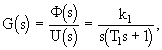
kde ![]() (s) je obraz úhlu natočení motoru [rad], U(s) - obraz napětí kotvy V, T1 - časová konstanta [s], k1 - koeficient přenosu motoru [rad.s-1.V1.]
(s) je obraz úhlu natočení motoru [rad], U(s) - obraz napětí kotvy V, T1 - časová konstanta [s], k1 - koeficient přenosu motoru [rad.s-1.V1.]
c) Identifikace pohybu manipulátoru
Budeme řídit natočení sloupu manipulátoru ![]() t za předpokladu, že rameno je ve střední poloze a neotáčí se, tzn. r(t)=0,5l=konst. Celkový moment setrvačnosti J je vlastně redukovaný moment na hřídel motoru, který otáčí sloupem. Redukovaný moment setrvačnosti
určíme na základě rovnosti kinetických energií, která je dána vztahem
t za předpokladu, že rameno je ve střední poloze a neotáčí se, tzn. r(t)=0,5l=konst. Celkový moment setrvačnosti J je vlastně redukovaný moment na hřídel motoru, který otáčí sloupem. Redukovaný moment setrvačnosti
určíme na základě rovnosti kinetických energií, která je dána vztahem
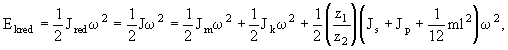
kde ![]() je úhlová rychlost [rad.s-1], Jm - moment setrvačnosti motoru [kg.m2], Jp - moment setrvačnosti pastorku [kg.m2], Jk - moment setrvačnosti ozubeného kola [kg.m2], m - hmotnost výsuvného ramena [kg], z1,z2 - počet zubů.
je úhlová rychlost [rad.s-1], Jm - moment setrvačnosti motoru [kg.m2], Jp - moment setrvačnosti pastorku [kg.m2], Jk - moment setrvačnosti ozubeného kola [kg.m2], m - hmotnost výsuvného ramena [kg], z1,z2 - počet zubů.
Z toho plyne
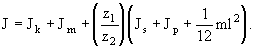
Sloup se otáčí přes čelní ozubené soukolí, proto vztah mezi úhlem natočení výstupního hřídele motoru a úhlem natočení sloupu je popsán
![]()
Po použití Laplaceovy transformace dostaneme vztah
![]()
kde A(s) je obraz úhlu natočení sloupu,![]() (s) - obraz úhlu natočení výstupního hřídele motoru.
(s) - obraz úhlu natočení výstupního hřídele motoru.
Regulace posuvu ramena manipulátoru
a) Stejnosměrný motor s konstantním buzením řízený proudem kotvy
Přenos regulované soustavy (motor + manipulátor, viz obr. 3.25)
![]()
Stupeń astatismu regulované soustavy je q = 2, tzn. jedná se o integrační soustavu druhého řádu bez setrvačnosti. Volíme proporcionálně-derivační regulátor (PD regulátor), který v našem případě můžeme v oblasti komplexní proměnné popsat rovnicemi
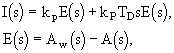
kde E(s) je obraz regulační odchylky, Aw(s)- obraz požadovaného vysunutí ramena, A(s) - obraz skutečnoho vysunutí ramena, kP - zesílení regulátoru [A.rad-1, TD - derivační časová konstanta [s].
Hodnoty stavitených parametrů kp a TD jsme určili na základě metody symetrického optima.
b) Stejnosměrný motor s konstantním buzením řízený napětím kotvy
Přenos regulované soustavy (motor + manipulátor, viz obr. 3.27)
![]()
Stupeń astatismu regulované soustavy je q = 1, tzn. jedná se o intagrační soustavu se setrvačností prvního řádu. Volíme proporcionální regulátor (P regulátor), který v našem případě můžeme v oblasti komplexní proměnné popsat rovnicemi
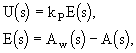
kde E(s) je obraz regulační odchylky, Aw(s) - obraz požadovaného vysunutí ramena, A(s) - obraz skutečnoho vysunutí ramena, kP - zesílení regulátoru [V.rad-1].
Hodnotu stavitelného parametru kp jsme určili pomocí metody optimalního modulu.
Simulační ověření
a) Motor řízený proudem kotvy {soubor SLPROUD.SIP}
Blokové schéma regulačního obvodu je na obr. 3.26 a jemu odpovídající simulační model je na
obr. 3.29.
Popis modelu:
| blok1 | - | realizuje žádanou veličinu ve tvaru skokové změny z hodnoty 0 na hodnotu Aw ,která nastane v čase t = 0, |
| blok 2 | - | sumátor, na jeho výstupu je rozdíl mezi žádaným a skutečným otočením sloupu manipulátoru, |
| bloky 3,4 | - | regulátor s omezením na maximální hodnotu proudu, |
| bloky 5, 6, 7 | - | regulovaná soustava, kde
|
| bloky 8, 9 | - | přičtení počáteční hodnoty natočení sloupu manipulátoru. |
Simulační výsledky na obr. 3.30. Cílem řízení bylo dosažení požadovaného
natočení sloupu manipulátoru. Vidíme, že po počátečních překmitech
se sloup dostal do požadované hodnoty 1,047rad v čase t=12,6s. Maximální překmit je k = 24,5![]() ,což odpovídá natočení sloupu o úhel 1,3032rad..
,což odpovídá natočení sloupu o úhel 1,3032rad..
Pro simulaci byly zvoleny tyto hodnoty:
m=96kg, l=1m, z1=20, z2=120, JS=0,232kg.m2,
JP=0,0006kg.m2, JK=0,00025kg.m2,
Jm=0,00046kg.m2, 0=0,628rad,
km=0,473N.m.A-1, Imax=13,6A,
k=2,413, kp=500, TD=0,1s.
b) Motor řízený napětím kotvy {soubor SLNAPETI.SIP}
Blokové schéma regulačního obvodu je na obr. 3.28 a jemu odpovídající simulační model je na
obr. 3.31.
Popis modelu:
| blok1 | - | realizuje žádanou veličinuve tvaru skokové změny z hodnoty 0 na hodnotu Aw, která nastane v čase t = 0, |
| blok 2 | - | sumátor, na jeho výstupu je rozdíl mezi žádaným a skutečným otočením sloupu manipulátoru, |
| bloky 3,4,5 | - | egulátor s omezením naminimální a maximální hodnotu napětí, |
| bloky 6,7,8 | - | regulovaná soustava, |
| bloky 9,10 | - | přičtení počáteční hodnoty natočení sloupu manipulátoru. |
Simulační výsledky na obr. 3.32. Cílem řízení bylo dosažení požadovaného
natočení sloupu manipulátoru. Vidíme, že po počátečním překmitu se sloup dostal do požadované hodnoty 1,047rad v čase
t=11,2s. Maximální překmit vysunutí ramena je 1,66![]() tzn., že sloup se natočí na odnotu 1,0644rad.
tzn., že sloup se natočí na odnotu 1,0644rad.
Pro simulaci byly zvoleny tyto hodnoty:
m=96kg, l=1m, z1=20, z2=120, JS=0,232kg.m2,
JP=0,0006kg.m2, JK=0,00025kg.m2,
Jm=0,00046kg.m2, 0=0,628m, km=0,473N.m.A-1,
Umax=149V, k1=2,1142, T1=0,372s,
kp=3,814.
Na obr. 3.33 je zásobník, do kterého se přivádí množství
![]() sypké hmoty dopravníkem. Na dopravník se
přivádí množství
sypké hmoty dopravníkem. Na dopravník se
přivádí množství ![]() . Přeprava sypké hmoty se děje konstantní rychlostí
. Přeprava sypké hmoty se děje konstantní rychlostí ![]() na dráze L = 100 m.
na dráze L = 100 m.
Ze zásobníku se odvádí množství ![]() a uvnitř zásobníku je zásoba m(t)[kg]. Navrhněte vhodný číslicový i analogový regulátor pro regulaci množství zásoby m(t) v zásobníku a seřiďte ho metodou inverze dynamiky.
a uvnitř zásobníku je zásoba m(t)[kg]. Navrhněte vhodný číslicový i analogový regulátor pro regulaci množství zásoby m(t) v zásobníku a seřiďte ho metodou inverze dynamiky.
Jako poruchu uvažujte odváděné množství ![]() .
.
Matematický model dopravníku
Předpokládejme ustálený průtok M = M1. Změní-li se přiváděné množství M v bodě 0 o ![]() , pak množství M1 v bodě 1 se změní až za dobu danou dopravním zpožděním TD o
, pak množství M1 v bodě 1 se změní až za dobu danou dopravním zpožděním TD o ![]() .
.
Platí tedy
![]()
Dopravní zpoždění je dáno vztahem
![]()
Provedeme Laplaceovu transformaci vztahu (3.43) a obdržíme
![]()
Matematický model zásobníku
Předpokládáme ustálený stav: M1= M2 = konst. a konstantní zásobu m. Zvětší-li se přiváděné množství M1 bude M1>M2, a zásoba m trvale poroste. Zásobník by se přeplnil. Jestliže naopak bude M1<M2, zásobník se bude vyprazdńovat do doby, než se úplně vyprázdní. Rychlost nárůstku nebo úbytku zásoby bude úměrná rozdílu M1- M2. Změna zásoby se řídí zákonem o zachování hmotnostního průtoku tj. rovnicí kontinuity.
Dále budeme uvažovat pouze změny od ustáleného stavu:![]()
Pro časovou změnu zásoby m platí
![]()
Po provedení Laplaceovy transformace vztahu (3.46) dostaneme:
![]()
Po dosazení vztahu (3.45) do (3.47) dostaneme
![]()
Volba regulátoru a jeho seřízení
a) analogový regulátor
Pro zadanou regulovanou soustavu volíme proporcionální
regulátor (P).
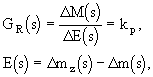
kde kp je zesílení regulátoru [m2.s-1] , mz(s) - obraz požadované zásoby [kg], E(s) - obraz regulační odchylky [kg]. Regulační obvod s analogovým regulátorem je na obr. 3.35.
Optimální hodnotu zesílení regulátoru jsme určili na základě metody inverze dynamiky.
b)číslicový regulátor
Pro zadanou regulovanou soustavu volíme proporcionální regulátor (P) o přenosu
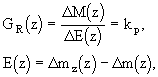
kde kp je zesílení regulátoru [m2.s-1] , mz(z) - obraz požadované zásoby [kg], E(z) - obraz regulační odchylky [kg]. Regulační obvod s analogovým regulátorem je na obr. 3.36.
Simulační model
a) analogový regulátor {soubor ZASOBA.SIP}
Blokové schéma regulačního obvodu je na obr. 3.35 a jemu odpovídající simulační model je na
obr. 3.37.
Pro simulaci byly zvoleny tyto hodnoty:
![]() mz = 20 kg,
mz = 20 kg,
![]() M2 = 0,02 kg.s-1,
M2 = 0,02 kg.s-1,
![]() Mmax = 0,2 kg.s-1, Td = 50s, kp = 0,0074.
Mmax = 0,2 kg.s-1, Td = 50s, kp = 0,0074.
b)číslicový regulátor {soubor ZASOBAD.SIP}
Blokové schéma regulačního obvodu je na obr. 3.36 a jemu odpovídající simulační model je na
obr. 3.39.
Pro simulaci byly zvoleny tyto hodnoty:
![]() mz = 20 kg,
mz = 20 kg, ![]() M2
= 0,02 kg.s-1,
M2
= 0,02 kg.s-1,![]() Mmax
= 0,2 kg.s-1, Td = 50s, kp =0,0067, T = 10s.
Mmax
= 0,2 kg.s-1, Td = 50s, kp =0,0067, T = 10s.
3.6. Literatura k regulačním obvodům
BALATĚ, J., FARANA, R., SMUTNÝ, L. a VÍTEČEK, A. 1993. Die Anwendung des Simulationssystems SIPRO fürSteuerungslösungen energetischer Prozesse. Wissenschaftliche Berichte Hochschule für Technik, Wirtschaft und Sozialwessen Zittau/Görlitz: 1993, Heft 34, S. 76 - 80. (BRD) 1
BOLTON, W. 1992. Control engineering. New York: Longman Scientific & Technical, 1992.
FARANA, R.1996. Univerzální simulační program SIPRO 3.4. Uživatelská příručka. Ostrava: katedra ATŘ VŠB Ostrava, 1996. 33
JULIŠ, K. a BREPTA, R. 1987. Mechanika, II. díl. Dynamika. Praha: SNTL, 1987.
NOSKIEVIČ, J. 1987. Mechanika tekutin. Praha: SNTL, 1987.
NOSKIEVIČ, P. 1992. Simulace systémů. Ostrava: ES VŠB, 1992. 6
NOVÁK, V. a ZÍTEK, P. 1982. Praktické metody simulace dynamických systémů. Praha: SNTL/ALFA, 1982. 7
ONDRÁČEK, E. a JANÍČEK, P. 1990. Výpočtové modely v technické praxi. Praha: SNTL, 1990. 8
SOUKUP, J. 1990. Identifikace soustav. Praha: SNTL, 1990.9
VEJRAŽKA, F. 1991. Signály a soustavy. Praha: ČVUT, 1991.10
VITÁSEK, E. 1987. Numerické metody. Praha: SNTL, 1987. 11
FARANA, R. 1996. Univerzální simulační program SIPRO 3.4. Uživatelská příručka. Ostrava: katedra ATŘ VŠB Ostrava, 1996. 1212
VÍTEČEK, A., FARANA, R., KAČMÁŘ, D., NĚMEC, R. a SMUTNÝ, L. 1991. Počítačová podpora výukového procesu v oblasti automatizace. Simulační program SIPRO-VÝUKA. (Výzkumná zpráva). Ostrava: FS VŠB, 1991.13
VÍTEČEK, A., FARANA, R. a SMUTNÝ, L. 1992. Simulation Program SIPRO and Experience of its Application to the Teaching. In Sborník konference "CAE in ACT". Praha: ČVUT, květen 1992, s.17.-20. 14
VÍTEČEK, A. a WAWRZICZKOVÁ, M. 1988. Teorie automatického řízení. Ostrava: ES VŠB, 1988. 15
ZÍTEK, P. 1990. Simulace dynamických systémů. Praha: SNTL, 1990. 16
ZÍTEK, P. 1993. Základy automatického řízení. Praha: ČVUT, 1993.
![]()