Je třeba analyticky popsat a simulačně ověřit proces hromadění (akumulaci, skladování) materiálu na skládce dle obr. 2.1, kde m(t) je celkové množství materiálu na skládce [kg], q1(t), resp. q2(t) je hmotnostní množství dovážené, resp. odvážené [kg s-1] (hmotnostní toky).
Matematický model
Pro elementární přírůstek množství materiálu na skládce dm(t) za elementární časový přírůstek dt platí bilanční rovnice
ze které po úpravě dostaneme lineární diferenciální rovnici 1. řádu
Je zřejmé, že množství materiálu na skládce nemůže být záporné, tj.
a že na skládce v čase t = 0 bylo určité počáteční množství
Integrací vztahu (2.1) při uvažování počáteční podmínky (2.3) dostaneme ekvivalentní vyjádření procesu hromadění materiálu na skládce
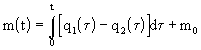
ze kterého vyplývá integrační (akumulační) charakter procesu hromadění materiálu, viz obr. 2.2.
Na základě vztahu (2.4) lze snadno analyzovat vlastnosti procesu hromadění materiálu, jak je ukázáno na obr. 2.3.
Ze vztahů (2.1) a (2.4) i z obr. 2.3 plyne, že ustálený výstup může vystoupit při libovolném množství materiálu na skládce mu -> 0 v tom případě, když
Bude-li navíc
pak vzniká ustálený stav celého procesu hromadění materiálu.
Je tedy zřejmé, že závislost mezi množstvím materiálu na skládce mu - výstupem a dováženým qu1a
odváženým qu2 množstvím - vstupy v ustáleném stavu neexistuje.
Použijeme-li Laplaceovou transformaci na vztah (2.1) při počáteční podmínce (2.3) nebo na vztah (2.4), dostaneme
kde jsou M(s), Q1(s) a Q2(s) obrazy příslušných veličin m(t), q1(t) a q2(t);
s - komplexní proměnná v Laplaceově transformaci.
Vztahu (2.6) odpovídá blokové schéma na obr. 2.4.
Simulační model
Simulační model procesu hromadění materiálu na skládce je na obr. 2.4a a výsledek simulace na obr. 2.4b. {soubor AKUMULAC.SIP}
Pro simulaci byly zvoleny tyto hodnoty:
m0 = 3000 kg; t0 = 1000 s; t1 = 2000 s; t2 = 4000
s; t3 = 5000 s, q1(t) = 01 kg s-1, q2(t) = 01 kg s-1.
Je třeba analyticky identifikovat regulovanou soustavu na obr. 2.5 a výsledky simulačně ověřit,
kde q1(t) je objemový přítok kapaliny [m3s-1], q2(t) - objemový odtok (odčerpávané průtočné
množství) [m3s-1] (objemové toky), h(t) - výška hladiny [m], P - plošný obsah hladiny [m2],
(t) - úhlová rychlost čerpadla [rad s-1], k1 - konstanta [m3rad-1].
Matematický model
Pro elementární přírůstek objemu kapaliny v nádrži Pdh(t) za elementární časový přírůstek dt platí bilanční rovnice
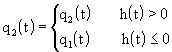
Po úpravě dostaneme diferenciální rovnici 1. řádu
resp.
s počáteční podmínkou (počáteční výškou hladiny)
Diferenciální rovnici (2.7) můžeme napsat v ekvivalentním integrálním tvaru
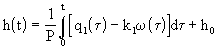
Nádrž s odčerpáváním na obr. 2.5 má vlastnosti integračního prvku, viz obr. 2.6.
Vzhledem k integračnímu charakteru regulované soustavy - nádrže s odčerpáváním neexistuje v ustáleném stavu závislost mezi
výstupem hu a vstupy qu1 a u , resp. qu2, tj.
regulovaná soustava na obr. 2.5 nemá statickou charakteristiku. Pro ustálený výstup platí
pro ustálený stav musí navíc platit
resp.
přičemž ustálená výška hladiny hu může mít jakoukoliv "rozumnou" kladnou hodnotu, protože pro výšku hladiny platí pouze omezení
kde je hmax maximální výška hladiny daná konstrukcí nádrže [m].
Po Laplaceově transformaci diferenciální rovnice (2.7) s počáteční podmínkou (2.8) nebo integrálního vztahu (2.9) získáme
popis vlastností nádrže s odčerpáváním v oblasti komplexní proměnné (obr. 2.7)
kde jsou H(s), Q1(s) a 
(s) obrazy příslušných
proměnných h(t), q1(t) a (t).
Časový průběh výšky hladiny h(t) v závislosti na přítoku q1(t) a odtoku q2(t) pro různé případy jsou na obr. 2.8.
Simulační model
Pro simulační ověření matematického modelu nádrže s odčerpáváním použijeme rovnici (2.9), případně blokové schéma na obr. 2.6. Abychom ukázali současně možnosti simulačního programu SIPRO, budeme uvažovat i omezení (2.12). Průběhy průtočných množství q1(t) a q2(t) namodelujeme podle obr. 2.8a {soubor NAD_O.SIP}
Horní omezení v nerovnosti (2.12) lze jednoduše modelovat pomocí bloku MAX, viz blok č. 10 na obr. 2.8b. Dolní omezení je složitější, protože musíme namodelovat podmínkový vztah
Slouží k tomu bloky č. 13 - 17.
Pro simulaci, jejíž výsledek je na obr. 2.8c byly zvoleny tyto hodnoty:
qu = 0,0002 m3s-1; h0 = 0,2 m; hmax = 0,3 m; P = 0,5 m2; t0 = 1
s; t1 = 30 s; t2 = 40 s ; t3 = 70 s.
Vyřešená regulace teto soustavy je v kapitole Regulace nádrže s odčerpáváním.
Provedeme analytickou identifikaci nádrže s volným odtokem kapaliny na obr. 2.9 a ověření výsledků simulací za předpokladu, že h(t) je výška hladiny [m], P - plošný obsah hladiny [m2], q1(t) je objemový přítok [m3s-1] a q2(t) je objemový odtok [m3s-1] (objemové toky), pro který platí
kde je a - konstantní koeficient průtoku [m5/2s-1].
Matematický model
Pro elementární přírůstek objemu kapaliny v nádrži Pdh(t) za elementární časový přírůstek dt platí bilanční rovnice
resp. po uvažování vztahu (2.14)
Po úpravě dostaneme nelineární diferenciální rovnici 1. řádu
s počáteční podmínkou
Je zřejmé, že nenulovou počáteční podmínku (2.16) mohl způsobit pouze nenulový přítok q1(t) pro t < 0. Pokud přítok q1(t) = 0 pro t < 0, pak rovněž h0 = 0.
V ustáleném stavu vymizí všechny změny v čase, tj.
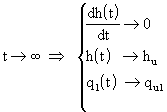
a proto ze vztahu (2.15) při uvažování (2.17) dostaneme
Vztah (2.19) vyjadřuje závislost mezi výškou hladiny hu a přítokem qu1 v ustáleném stavu. Je to statická charakteristika, která je definována pouze v 1. kvadrantu, protože platí fyzikální omezení výšky hladiny (obr. 2.10)
kde je hmax maximální výška hladiny daná konstrukcí nádrže [m].
Blokové schéma nádrže s volným odtokem odpovídající diferenciální rovnici (2.15) je na obr. 2.11.
V regulační technice se často používá linearizace, protože u lineárních modelů můžeme s výhodou použít Laplaceovou transformaci a celé řady jiných metod, které neplatí pro nelineární modely.
Použijeme přírůstkové proměnné vyjadřující přírůstky od zvolených ustálených hodnot, které určují tzv. pracovní bod (stav), viz
obr. 2.10:
Po dosazení (2.20) a (2.21) do nelineární diferenciální rovnice (2.15) dostaneme
Použijeme linearizaci pomocí Taylorova rozvoje
a po jednoduché úpravě obdržíme lineární diferenciální rovnici 1. řádu
kde je T1 - časová konstanta [s],
k1 - koeficient přenosu [m-2s].
Statickou charakteristiku v přírůstkových proměnných získáme z diferenciální rovnice (2.23a) snadno, protože platí
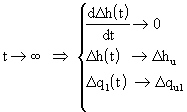
a tedy
Vidíme, že koeficient přenosu k1 vyjadřuje směrnici (sklon) statické charakteristiky v přírůstkových proměnných (souřadnicích), viz obr. 2.10 a 2.12.
Z diferenciální rovnice (2.23a) vyplývá, že nádrž s volným odtokem po linearizaci má vlastnosti proporcionálního prvku se setrvačností
1. řádu. Při práci s linearizovaným modelem (2.23) je třeba pamatovat, že platí pro malé odchylky od zvoleného pracovního bodu, jehož souřadnice jsou dány vztahem (2.19). Proto je třeba vždy uvážit, zda se bude pracovat v přírůstkových proměnných,
pak se použije blokové schéma na obr. 2.13a, nebo v původních proměnných, kdy je
nutno použít blokové schéma z obr. 2.13b.
Použitím Laplaceovy transformace (při nulové počáteční podmínce) na diferenciální rovnici (2.23a) a úpravě dostaneme
kde jsou H(s), 
Q1(s) obrazy příslušných
proměnných h(t), q1(t).
V regulační technice vztah (2.26) zapisujeme pomocí přenosu
Simulační model
U nádrže s volným odtokem využijeme simulačního ověření matematického modelu i pro srovnání přesného nelineárního matematického modelu (2.15) pro h0 = hu (viz také obr. 2.11) a linearizovaného matematického modelu (2.23) (viz také obr. 2.13). V simulačním modelu na obr. 2.15 jsou uvažovány současně oba matematické modely a dále závislost (2.19) vyjadřující vztah mezi výškou hladiny a přítokem v ustáleném stavu. Na základě této závislosti jsou pak uvažovány parametry (2.23b) a (2.23c) linearizovaného modelu (2.23a). Pracovní bod linearizovaného modelu je určen právě zvoleným stavem (obr. 2.10). V našem případě budeme vycházet ze zvolené hodnoty ustálené výšky hladiny hu > 0 {soubor NAD_P.SIP}. Výsledky simulace jsou ukázány na obr. 2.16. Z průběhů vidíme, že rozdíly mezi oběma dvěma modely pro dané podmínky jsou zanedbatelně malé. Můžeme tedy říci, že pro daný pracovní bod linearizace je oprávněná.
Pro simulaci byly zvoleny tyto hodnoty:
t0 = 1 s; t1 = 30 s; t2 = 60 s; t3 = 90 s; P = 0,5 m2;
hu = 0,2 m; a = 0,00044 m5/2s-1.
Vyřešená regulace teto soustavy je v kapitole Regulace nádrže s volným odtokem.
Uvažujeme rekuperátor pro ohřev vzduchu (obr. 2.17) jako regulovanou soustavu. Výstupní veličinou je teplota vzduchu vv [K]. Vzduch prochází trubkou, která je obtékána kouřovými plyny (spalinami). Určíme přenos rekuperátoru a jeho adekvátnost ověříme simulací.
Řešení
Budeme předpokládat, že výměna tepla se uskutečňuje vedením: od kouřových plynů přes stěnu trubky se součinitelem
přestupu tepla a1 [W m-2K-1] a od trubky přes její vnitřní stěnu
se součinitelem přestupu tepla a2 [W m-2K-1]. Dále
předpokládáme, že rozdíl teplot na stěnách trubky je zanedbatelně malý (tj. trubku považujeme za tepelně "tenké" těleso).
Matematický model
Z rovnosti tepelných toků kouřové plyny - trubka dostaneme
kde je
vs - teplota (stěny) trubky rekuperátoru [K],
vp - teplota kouřových plynů [K],
VS - objem trubky rekuperátoru [m3],
S - hustota trubky rekuperátoru [kg m-3],
cS - měrná tepelná kapacita trubky rekuperátoru [J kg-1K-1],
P1 - vnější povrch trubky rekuperátoru obtékaný proudícími kouřovými plyny [m2].
Rovnici (2.28) upravíme a dostaneme
kde je Ts - časová konstanta [s].
Podobně z rovnosti tepelných toků trubka - vzduch obdržíme
kde je
Tv - časová konstanta [s],
Vv - objem ohřívaného vzduchu [m3],
v- hustota ohřívaného vzduchu [kg m-3],
cv- měrná tepelná kapacita ohřívaného vzduchu [J kg-1K-1],
P2- vnitřní povrch trubky rekuperátoru obtékaný vzduchem [m2].
Použitím Laplaceovy transformace na vztahy (2.29a) a (2.30a) za předpokladu nulových počátečních podmínek obdržíme odpovídající přenosy:
dílčí přenos "kouřové plyny - trubka"
dílčí přenos "trubka - vzduch"
Výsledný přenos rekuperátoru jako regulované soustavy je dán součinem dílčích přenosů (2.31) a (2.32).
Vidíme, že rekuperátor se chová jako nekmitavá proporcionální soustava se setrvačností 2. řádu. Pro simulační účely je vhodné pracovat
s přírůstky, např. od teploty okolí 
0, tj.
v(t) = v(t) - 0,
s(t) = s(t) - 0,
p(t) = p(t)
- 0. Protože se jedná o lineární regulovanou soustavu, tvary přenosů se nezmění,
viz obr. 2.18.
Simulační model
Simulační model v tomto případě je velmi jednoduchý, protože simulační program SIPRO obsahuje blok typu SET, který přímo
realizuje přenos (2.31), resp. (2.32) pro obrazy odpovídajících přírůstků teplot.
Výsledky simulace pro skokové změny teploty kouřových plynů p(t)
jsou na obr. 2.20 a potvrzují správnost zjednodušujících předpokladů a matematických modelů (2.31) - (2.33)
Pro simulaci byly zvoleny tyto hodnoty:
t1 = 1 s; t2 = 1500 s;
p = 80 K;
0 = 293 K = 20 C, Ts = 210 s; Tv = 150 s.
Určíme matematický model stejnosměrného motoru (obr. 2.21) řízeného proudem kotvy,
resp. napětím kotvy za předpokladu, že celková indukčnost kotvy je zanedbatelně malá a že buzení je konstantní. Jako výstupní veličiny budeme uvažovat úhlovou rychlost a úhlové natočení hřídele motoru.
Význam označení na obr. 2.21: ua(t) - napětí kotvy [V], ia(t) - proud kotvy [A],
Ra - celkový odpor kotvy [], mh(t) - hnací moment [N m],
mz(t) - zátěžný moment [N m], J - celkový moment setrvačnosti [kg m2],
j - konstantní magnetický tok [Wb], (t) - úhlová
rychlost [rad s-1], j(t) - úhlové natočení [rad].
Matematický model
a) Stejnosměrný motor řízený proudem kotvy
Základní pohybová rovnice pro motor má tvar
U stejnosměrného motoru s konstantním buzením hnací moment mh(t) je přímo úměrný proudu kotvy ia(t), proto lze psát
kde km je momentová konstanta motoru [N m A-1].
Mezi úhlovou rychlostí (t) a úhlovým natočením j(t) platí jednoduchý vztah
Použijeme Laplaceovou transformaci za předpokladu nulových počátečních podmínek na vztahy (2.34) - (2.36) a dostaneme
V souladu se zvyklostmi obrazy jsou označené velkými písmeny. Odpovídající blokové schéma je na obr. 2.22.
Vyjádříme ještě dílčí přenosy motoru pro úhlovou rychlost (t) i úhlové natočení j(t). Můžeme vycházet z obr. 2.22 nebo vztahů (2.37) - (2.39):
Vidíme, že stejnosměrný motor s cizím konstantním buzením řízený proudem kotvy lze považovat za integrační člen 1., resp. 2. řádu v závislosti na výstupní
veličině. Znaménko "-" v přenosech (2.41) a (2.43) vyjadřuje tu skutečnost, že při zvětšení zátěžného
momentu mz(t) dochází k poklesu jak úhlové rychlosti (t), tak i úhlového
natočení j(t).
b) Stejnosměrný motor řízený napětím kotvy
V tomto případě navíc musíme uvažovat rovnici
jejíž Laplaceův obraz má tvar
Pomocí vztahů (2.37) - (2.39) a (2.44) lze sestavit blokové schéma stejnosměrného motoru s konstantním buzením řízeného napětím kotvy, viz obr. 2.23.
Na základě vztahů (2.37) - (2.39) a (2.44),
resp. obr. 2.23 můžeme snadno určit dílčí přenosy pro výstupní úhlovou rychlost
(t) a úhlové natočení j(t):
kde je
T1 - elektromagnetická časová konstanta motoru [s],
k1 - koeficient přenosu motoru [rad s-1V-1],
k2 - momentový koeficient přenosu motoru [rad s-1N-1m-1].
Z dílčích přenosů (2.46) -
(2.49) vyplývá, že pro výstupní úhlovou rychlost (t) stejnosměrný motor řízený
napětím kotvy ua(t) má vlastnosti proporcionálního členu se setrvačností 1. řádu a pro výstupní úhlové
natočení (t) má vlastnosti integračního členu se setrvačností 1. řádu.
Simulační model
a) Stejnosměrný motor řízený proudem kotvy {soubor KOT_PRO.SIP}
Simulační schéma stejnosměrného motoru s konstantním buzením řízeného proudem kotvy je velmi jednoduché (obr. 2.24). Můžeme použít jak dílčích přenosů (2.40) - (2.43), tak i blokového schématu na obr. 2.22. Jako vstupní signály použijeme pravoúhlé impulsy.
Pro simulaci byly zvoleny tyto hodnoty:
t1 = 1 s; t2 = 4 s; t3 = 12 s; t4 = 16 s; ia = 4 A; km = 2 N m A-1;
J = 2 kg m2; mz = 4 N m.
b) Stejnosměrný motor řízený napětím kotvy {soubor KOT_NAP.SIP}
Rovněž v tomto případě simulační schéma je velmi jednoduché. Vyjdeme-li z přenosů (2.46) - (2.49), pak simulační schéma má
tvar jak na obr. 2.26.
Pro napětí kotvy ua(t) použijeme skokovou změnu a pro zátěžný moment mz(t) pravoúhlý impuls. Výsledky simulace jsou na obr. 2.27.
Pro simulaci byly zvoleny tyto hodnoty:
t1 = 1 s; t2 = 10 s; t3 = 13 s; t4 = 16s; ua = 6 V; k1
= 2 rad s-1V-1; k2 = 3 rad s-1 N-1 m-1; T1 = 2 s; km = 2 N m A-1; J = 2 kg m2; mz = 4 N m.
Regulace, která využívá poznatky této kapitoly je v kapitole Regulace vysunutí ramena manipulátoru a Regulace natočení sloupu manipulátoru.
BALATĚ, J., FARANA, R., SMUTNÝ, L. a VÍTEČEK, A. 1993. Die Anwendung des Simulationssystems
SIPRO für Steuerungslösungen energetischer Prozesse. Wissenschaftliche Berichte Hochschule für Technik. Wirtschaft und Sozialwessen Zittau/Görlitz, 1993. Heft 34, S. 76 - 80. (BRD)
NOSKIEVIČ, J. 1987. Mechanika tekutin. Praha: SNTL, 1987.
NOSKIEVIČ, P. 1992. Simulace systémů. Ostrava: ES VŠB, 1992.
NOVÁK, V. a ZÍTEK, P. 1982. Praktické metody simulace dynamických systémů. Praha: SNTL/ALFA, 1982.
ONDRÁČEK, E. a JANÍČEK, P. 1990. Výpočtové modely v technické praxi. Praha: SNTL, 1990.
SOUKUP, J. 1990. Identifikace soustav. Praha: SNTL, 1990.
VEJRAŽKA, F. 1991. Signály a soustavy. Praha: ČVUT, 1991.
FARANA, R. 1996. Univerzální simulační program SIPRO 3.4. Uživatelská příručka. Ostrava: katedra ATŘ VŠB Ostrava, 1996.
VÍTEČEK, A. a WAWRZICZKOVÁ, M. 1988. Teorie automatického řízení. Ostrava: ES VŠB, 1988.
ZÍTEK, P. 1990. Simulace dynamických systémů. Praha: SNTL, 1990. 10
ZÍTEK, P. 1993. Základy automatického řízení. Praha: ČVUT, 1993.
