5. Filtrace u lineárních diskrétních regulačních obvodů

U diskrétního PSD regulátoru probíhá výpočet akčního zásahu přesně dle příslušné diferenční rovnice. Toto má za následek, že nedochází k přirozenému útlumu velkých a prudkých změn hodnot regulační odchylky a tím i akční veličiny, jako je tomu u spojitých regulačních obvodů.

U spojitých PID regulátorů vlivem setrvačnosti dochází k přirozené filtraci šumu a jeho vysokofrekvenčních složek. Setrvačnost je také jakýmsi zpožďovacím faktorem při skokových změnách žádané hodnoty a proto je nebezpečí vzniku prudkých změn akční veličiny menší u spojitých systémů než u diskrétních.

U číslicových regulátorů dochází k velkým změnám akční veličiny prakticky vždy, když se více změní regulační odchylka. Díky šumu, který doprovází signál nesoucí informaci o regulované veličině, dochází k tomu, že přenášený signál je zatížen náhodnou chybou [Švarc, Šeda, Vítečková, 2007].

Abychom zabránili negativním vlivům prudkých změn regulační odchylky, využíváme filtrů, které fyzicky zařadíme před číslicový PSD regulátor a nebo upravíme algoritmus samotného číslicového PSD regulátoru.

5.1 Filtrace vzorkované veličiny

Diferenční rovnice filtru 1. řádu je

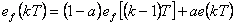(5.1)

kde

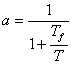(5.2)

je koeficient filtrace.

Pokud je a = 1 vstupní veličina není filtrovaná a pokud a = 0 je vstupní signál odpojen.

Jak již bylo zmíněno, je možné zabránit negativním vlivům prudkých změn regulační odchylky také úpravou algoritmu číslicového PSD regulátoru daného vztahem

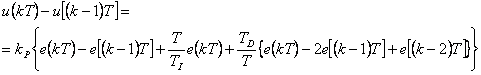(5.3)

Není vhodné, aby v tomto vztahu byla zastoupena pouze regulační odchylka 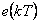. Ve většině případů je žádaná veličina konstantní a při její občasné změně není nutné, aby byla znovu derivovaná a tato změna vnesla do řízení nevhodný účinek [Švarc, Šeda, Vítečková, 2007]. Tím pádem je po úpravě možno získat alternativu vztahu (5. 3).

Pro 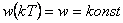platí

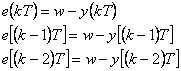	(5.4)
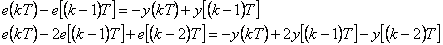	(5.5)

a nyní můžeme získat alternativu vztahu PSD regulátoru

(5.6)

Potlačení vzniku velkých změn akční veličiny v důsledku diskrétní realizace spojité derivace na šumem zatížené regulační odchylce 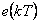se provádí přímo v algoritmu náhrady derivace. Místo ideální spojité derivace 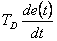se provádí náhrada členem 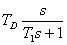, tedy derivačním členem se setrvačností prvního řádu, který funguje jako filtr. Toto řešení je výhodnější než použití filtru před regulátorem, protože filtrace se týká pouze derivační složky a nevnáší setrvačnost do proporcionální a sumační složky [Švarc, Šeda, Vítečková, 2007].