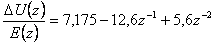4. Konvenční typy lineárních diskrétních regulátorů a jejich modifikace
Základní funkcí regulátoru v regulačním obvodu je vytvářet akční veličinu 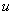 na základě regulační odchylky
na základě regulační odchylky 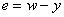 . Akční veličina má za úkol svým působením na regulovanou soustavu v každém časovém okamžiku zajišťovat to, aby byla regulační odchylka co nejmenší bez ohledu na poruchovou veličinu v.
. Akční veličina má za úkol svým působením na regulovanou soustavu v každém časovém okamžiku zajišťovat to, aby byla regulační odchylka co nejmenší bez ohledu na poruchovou veličinu v.
Pro spojité regulátory P, I, PI, PD, PID budou uvedeny jejich číslicové verze, které se označují P (proporcionální), S (sumační), PS (proporcionálně sumační), PD (proporcionálně diferenční), PSD (proporcionálně sumačně diferenční).
4.1 Algoritmy číslicových regulátorů
Od číslicového regulátoru požadujeme stejnou funkci jako od regulátoru spojitého, a proto vycházíme z rovnice spojitého PID regulátoru (4. 1).
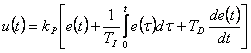 |
(4.1) |
Číslicovou verzi tohoto regulátoru získáme, když integrál nahradíme sumací (4. 2) a derivaci nahradíme zpětnou diferencí (4. 3).
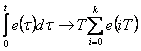 |
(4.2) |
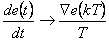 |
(4.3) |
Číslicový (diskrétní) regulátor je tedy dán obecným vztahem (4. 4).
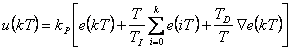 |
(4.4) |
kde 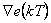 je zpětná diference definovaná vztahem (4. 5).
je zpětná diference definovaná vztahem (4. 5).
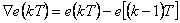 |
(4.5) |
Tomuto algoritmu číslicového regulátoru se říká polohový algoritmus. Hodnota integrálu se získává sumací a hodnota derivace se získává pomocí diference. Proto se tyto regulátory nazývají proporcionálně-sumačně-diferenční, a označují zkratkou PSD. Setkáme se taky s označením číslicové PID regulátory. Polohový algoritmus se příliš často nepoužívá hlavně kvůli sumaci, která znamená komplikaci při výpočtu akční veličiny  [Švarc, 2002].
[Švarc, 2002].
Z-přenos polohového algoritmu PSD regulátoru tedy je
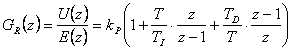 |
(4.6) |
Ostatní přenosy regulátorů a algoritmy jsou uvedeny v tab. 4. 1.
| Regulátor | Diferenční rovnice - absolutní (polohové) vyjádření | Z-přenos |
| P | 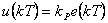 |
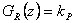 |
| S (číslicový I) | 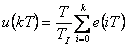 |
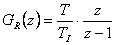 |
| PS (číslicový PI) | 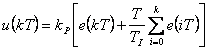 |
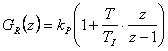 |
| PD | 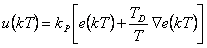 |
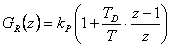 |
| PSD (číslicový PID) | 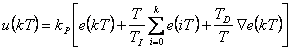 |
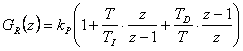 |
Nyní přejdeme k přírůstkovému algoritmu PSD regulátoru. Podle tohoto algoritmu se určuje nikoliv hodnota akční veličiny 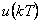 v daném okamžiku, ale pouze její změna, čili přírůstek oproti hodnotě
v daném okamžiku, ale pouze její změna, čili přírůstek oproti hodnotě 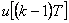 akční veličiny v předchozím kroku. Přírůstkové algoritmy můžeme použít pouze tehdy, když je obsažena sumační činnost (S, PS, PSD), protože jenom u této činnosti vystupuje regulační odchylka
akční veličiny v předchozím kroku. Přírůstkové algoritmy můžeme použít pouze tehdy, když je obsažena sumační činnost (S, PS, PSD), protože jenom u této činnosti vystupuje regulační odchylka 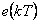 , viz (4. 9).
, viz (4. 9).
Diferenční rovnice PSD pro diskrétní čas 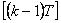 je vyjádřena vztahem (4. 7).
je vyjádřena vztahem (4. 7).
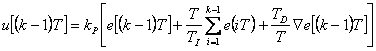 |
(4.7) |
Diferenční rovnice PSD pro diskrétní čas 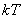 je vyjádřena vztahem (4. 8).
je vyjádřena vztahem (4. 8).
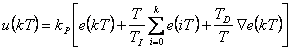 |
(4.8) |
Po odečtení těchto dvou vztahů získáme PSD regulátor pro přírůstkový algoritmus.
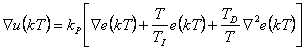 |
(4.9) |
kde
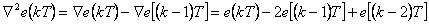 |
(4.10) |
Po dosazení získáme konečný tvar PSD regulátoru (4. 11) a po úpravě (4. 12).
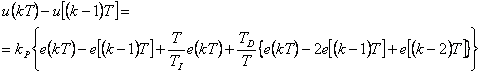 |
(4.11) |
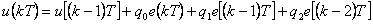 |
(4.12) |
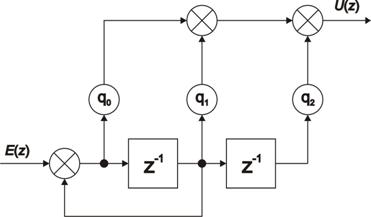
Po úpravě vztahů (4. 12) a (4. 14) určíme přenos PSD regulátoru pro přírůstkový algoritmus při použití Z-transformace.
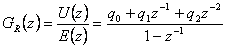 |
(4.13) |
kde
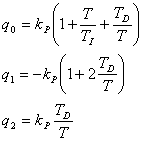 |
(4.14) |
Někdy se pro sumační činnost používá lichoběžníkova sumace.
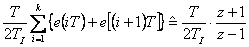 |
(4.15) |
Příklad 4.1
Převeďte spojitý regulátor s přenosem 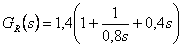 na číslicový PSD regulátor s přírůstkovým algoritmem při vzorkovací periodě T = 0,1 s. Odvoďte jeho diferenční rovnici a Z-přenos.
na číslicový PSD regulátor s přírůstkovým algoritmem při vzorkovací periodě T = 0,1 s. Odvoďte jeho diferenční rovnici a Z-přenos.
Řešení:
- Z přenosu určíme následující konstanty:
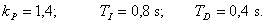
- Nyní můžeme určit
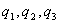 .
. - Diferenční rovnice dle (4. 12) tedy bude
- Z-přenos je dle (4. 14)
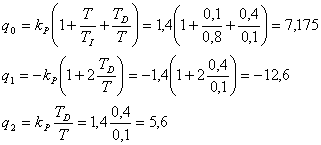
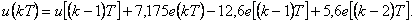
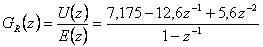
příp.