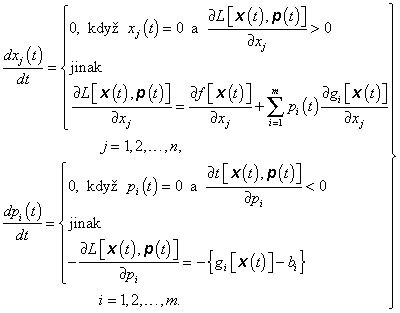3 Statická optimalizace funkcí více proměnných

3.4 Zhodnocení metod vícerozměrné optimalizace

Analytické metody vícerozměrné optimalizace jsou sice nekonstruktivní (tj. ukazují, jakým podmínkám má řešení vyhovovat, ale neukazují, jak toto řešení získat), ale přesto mají veliký význam jak teoretický, tak i praktický. V případě neveliké dimenze n dovolují poměrně snadno vyhledat optimální řešení, viz příklady v kap. 3. Mohou být rovněž přímo využity pro řešení konkrétních optimalizačních úloh na samočinných počítačích. Např. z Kuhnových-Tuckerových podmínek vychází následující gradientní metoda:

Řešením soustavy n + m diferenciálních rovnic (3.111), ve kterých účelová funkce f(x) a omezující funkce {g_i(x)} jsou ryze konvexní, proměnné x(t) a Lagrangeovy multiplikátory p(t) jsou časové funkce a počáteční podmínky jsou nezáporné, tj.  a , získáme řešení úlohy minimalizace

Dualita optimalizačních úloh má velice důležitou ekonomickou interpretaci. V technické praxi se využívají především při řešení úloh lineárního programování. Rovněž veliký prakticky význam má interpretace Lagrangeových multiplikátorů jako citlivostních charakteristik optimální hodnoty účelové funkce ke změnám příslušných omezujících konstant.

Největší předností analytických metod je možnost současného získání kvalitativních i kvantitativních změn optimálního řešení při změnách některých parametrů optimalizační úlohy.

Při veliké dimenzi n je nutno optimalizační úlohy řešit na samočinných počítačích.