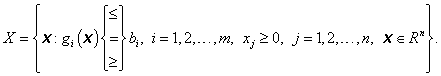1 Úvod do optimalizace

1.3 Klasifikace matematických metod řešení úloh optimalizace

Klasifikace metod řešení úloh statické a dynamické optimalizace je velmi složitým problémem a má vždy charakter určité domluvy. Proto také každá klasifikace má své nedostatky.

Základní rozdělení metod statické a dynamické optimalizace:

a) Analytické metody – využívají výsledků klasických i neklasických metod diferenciálního a variačního počtu.

b) Numerické (algoritmické) metody – využívají každou předcházející informaci v iteračním procesu ke zlepšení řešení, přičemž se pracuje s konkrétními numerickými hodnotami.

c) Grafické metody – jsou založeny na grafickém zobrazení dané optimalizační úlohy a na její grafické analýze.

d) Experimentální metody – experimentuje se přímo s reálnými objekty (veličinami), přičemž výsledky předcházejícího experimentu jsou využívány k plánování následujícího experimentu, což umožňuje dosáhnout zlepšení řešení.

V úlohách statické optimalizace (matematického programování) množina přípustných řešení je nejčastěji tvořena omezujícími (vazebními) funkcemi , omezujícími (vazebními) konstantami   a podmínkami nezápornosti proměnných , tj.

Jsou-li omezující funkce ve vztahu (1.47) a účelová funkce lineární, tj.

přičemž koeficienty a_ij, b_i a c_j, a jsou známé konstanty, pak jde o úlohu lineárního programování. Ve všech zbývajících případech jde o úlohy nelineárního programování.

Pro řešení úloh lineárního programování existuje celá řada metod. Nejznámější a nejuniverzálnější je simplexová metoda.

Pro řešení úloh nelineárního programování neexistuje podobná univerzální metoda. Ke každému nelineárnímu problému je třeba přistupovat zvlášť a při jejich řešení je nutno uvažovat všechny vlastnosti účelové funkce f(x) a množiny přípustných řešení X. Proto úlohy nelineárního programování se dělí z hlediska možných metod řešení.

Speciální, velmi důležitou, třídu úloh nelineárního programování tvoří případy, kdy množina přípustných řešení je celý n-rozměrný euklidovský prostor, tj.

V tomto případě hovoříme o úlohách na volný extrém nebo optimalizačních úlohách bez omezení.

Je-li množina přípustných řešení X tvořena rovnostmi

pak jde o klasickou úlohu na vázaný extrém nebo optimalizační úlohu s omezeními ve tvaru rovností.

Úlohy nelineárního programování s množinou přípustných řešení X v obecném tvaru (1.47) se nazývají úlohy na vázaný extrém nebo optimalizační úlohy s omezeními ve tvaru rovností a nerovností.

Je-li účelová funkce f(x) a množina přípustných řešení X konvexní, pak hovoříme o konvexním programování, v opačném případě – o nekonvexním programování.

Úlohami dynamické optimalizace se v těchto textech zabývat nebudeme. K jejich řešení slouží v podstatě tři metody ve verzi jak spojité, tak i diskrétní: variační počet, princip maxima (minima) a dynamické programování. V poslední době i k úlohám dynamické optimalizace se stále častěji používají metody nelineárního programování.