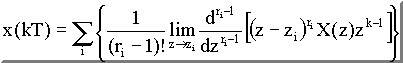
Příklad 4
Předchozí příklad vyřešíme pomocí metody reziduí :
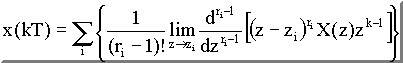
Vz. 33
Řešení :
Po úpravě (Vz. 32) a dosazení počátečních podmínek (Vz. 30) dostaneme :
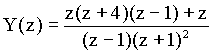
Kde počet různých kořenů je 2 (i = 1, 2); z1 = 1, z2 = -1; násobnost kořenů r1 =1, r2 =2, stupeň mnohočlenu ve jmenovateli obrazu n = r1 + r2 = 3, potom
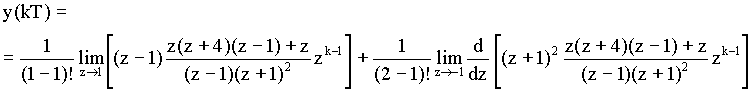
Po úpravě a derivaci dostaneme :
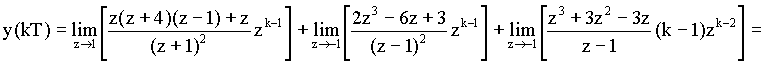
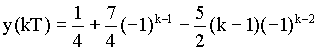
Výsledek jsme získali opět v uzavřeném tvaru. Pro k = 0, 1, 2,…dostaneme :
y(0) = 1
y(T) = 2
y(2T) = -4
y(3T) = 7
y(4T) = -9