Příklad 3

Pomocí transformace Z vyřešíme lineární diferenční rovnici 2. řádu

Vz. 29

při počátečních podmínkách

y(0) = 1; y(T) = 2

Vz. 30

a pro vstupní diskrétní funkci

u(kT) = h (kT).

Vz. 31

Řešení :

Na danou diferenční rovnici použijeme Z-transformaci (vlastnost Vz. 15d)

a po úpravě dostaneme

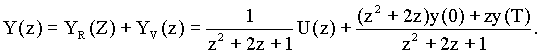
Vz. 32

Protože pro danou diferenční rovnici nebyly použity počáteční podmínky pro pravou stranu (pravá strana neobsahuje posunutou vstupní funkci), proto je volná část řešení současně homogenním řešením, tj. Y_V(z) = Y_H(z).

Po dosazení počátečních podmínek (Vz. 46) a obrazu vstupní diskrétní funkce

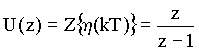      obdržíme

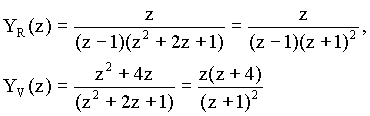
Originál řešení můžeme získat rozvojem obrazu řešení Y(z) v mocninou řadu (nekonečným dělením čitatele jmenovatelem) :

Po úpravě a dosazení počátečních podmínek dostaneme

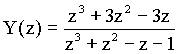
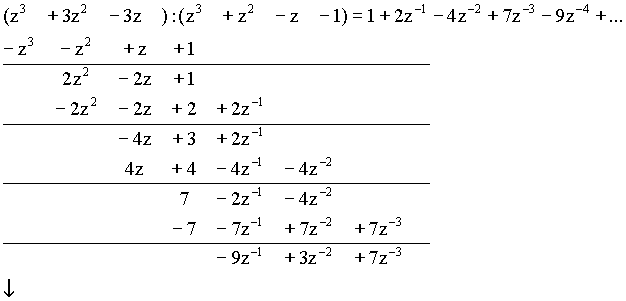
Výsledek jsme získali v otevřeném tvaru. Pro k = 0, 1, 2, … dostaneme :

y(0) = 1

y(T) = 2

y(2T) = -4

y(3T) = 7

y(4T) = -9

Abychom určili celé řešení (tj. v uzavřeném tvaru), musíme obraz řešení rozložit na parciální zlomky :

Obraz Y(z) je výhodné vynásobit    

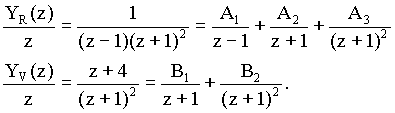
Pro určení konstant A₁, A₂, A₃, B₁ a B₂ použijeme dosazovací metodu :

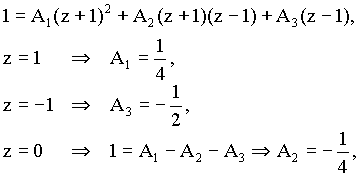
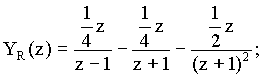
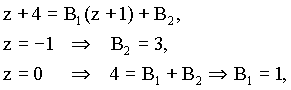
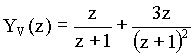
Ze slovníku Z-transformace (Příloha) snadno najdeme originály :

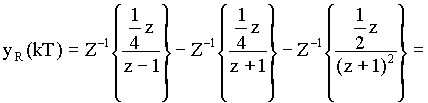
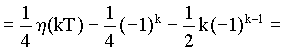
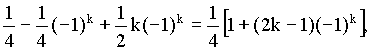
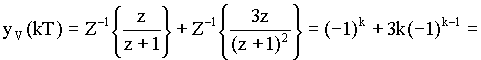
Řešení diferenční rovnice má tedy tvar

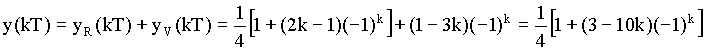
Výsledek jsme získali v uzavřeném tvaru. Pro k = 0, 1, 2,…dostaneme :

y(0) = 1

y(T) = 2

y(2T) = -4

y(3T) = 7

y(4T) = -9