V následující kapitole budou popsány možnosti vykreslení základních charakteristik systému:
Přechodová charakteristika je odezva systému na jednotkový (Haevisideův) skok na vstupu. Je to tedy časový průběh výstupní veličiny systému a značí se h(t). Jednotkový skok je funkce, která do času t=0 má nulovou hodnotu a v čase t=0 skočí její hodnota na jednotku, kterou pak stále udržuje.[Švarc, I. 1992]
Více informací naleznete v publikaci: Prezentační a výukový modul pro oblast analýzy regulačních obvodů.
V programu Matlab můžeme přechodovou charakteristiku vykreslit příkazem step, nebo pomocí příkazu ltiview s parametrem step. Tyto příkazy zadáváme v následujících tvarech:
step(SYS) ltiview(‘step’,SYS) |
Provedeme porovnání přechodových charakteristik u tří proporcionálních systémů, které máme zadány přenosy:
1. proporcionální člen bez setrvačnosti (ideální) - ![]()
2. proporcionální člen se setrvačností 1. řádu - ![]()
3. proporcionální člen se setrvačností 2. řádu - ![]()
Pro zadání všech tří přenosů použijme příkaz tf:
p = tf(0.9, 1) p1 = tf([1], [3 1]) p2 = tf([5 1], [7 3 5]) |
Přechodové charakteristiky vykreslíme pomocí příkazu step.
step(p, p1, p2) |
Pomocí příkazů title,xlabel a ylabel můžeme do grafu zadat titulek a popis osy xa y.
title('Prechodova charakteristika')
ylabel('h(t)')
xlabel('cas[s]')
|
Výsledný graf je na obr. 2.27, popisky jednotlivých charakteristik byly přidány dodatečně pomocí příkazů z panelu nástrojů dialogového okna grafu. Pomocí dalších nabídek tohoto dialogového okna je možné měnit i některé další zobrazené informace např. zobrazení mřížky, popisky os a titulku, barvy vykreslených grafů a další.
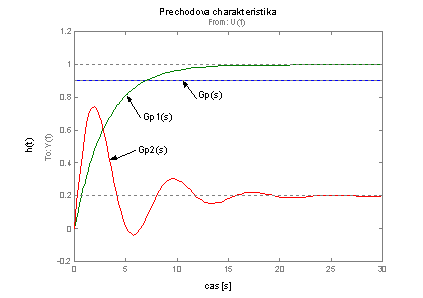
obr. 2.27 Vykreslení přechodových charakteristik proporcionálních systémů
vykr_step_P.m - vykreslení prechodové charakteristiky proporcionálních systémů (m-file)
Pro vykreslení přechodových charakteristik pomocí programu imulink budeme potřebovat bloky Transfer Fnc pro každý přenos, generátor vstupního signálu Step, pro spojení výsledných dat blok Mux a pro zobrazení dat blok Scope. Do bloků Transfer Fnc zadáme hodnoty jednotlivých přenosů a bloky propojíme podle schématu na obr. 2.28.
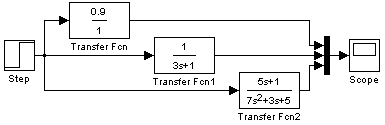
obr. 2.28 Blokově schéma programu Simulink - vykresleni h(t) pro proporcionální člen
sim_step_P.mdl - vykreslení prechodové charakteristiky proporcionálních systémů (Simulink)
Provedeme porovnání přechodových charakteristik u tří integračních systémů, jež máme zadány přenosy:
1. Integrační člen bez setrvačnosti (ideální) - ![]()
2. Integrační člen se setrvačností 1. řádu - ![]()
3. Integrační člen 2. řádu se setrvačností 1.řádu - ![]()
Přenosy zadáme pomocí příkazu tf:
i = tf([1],[1 0]); i1 = tf([1], [1 1 0]); i2 = tf([1], [1 1 0 0]) |
Pro vykreslení charakteristik použijeme příkaz step:
step(i, i1, i2) |
Výsledný graf ke kterému byly přidány popisky os a titulek je na obr. 2.29.
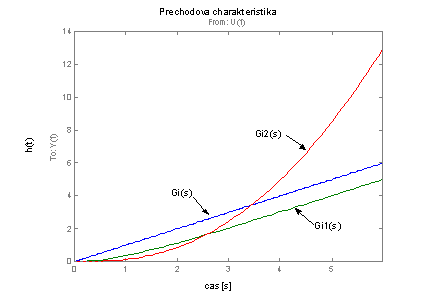
obr. 2.29 Vykreslení přechodových charakteristik integračních systémů
vykr_step_I.m - vykreslení prechodové charakteristiky integračních systémů (m-file)
Pro vykreslení přechodových charakteristik pomocí programu Simulink budeme potřebovat bloky Transfer Fnc, Step, Mux a Scope. Bloky propojíme podle schématu na obr. 2.30 .
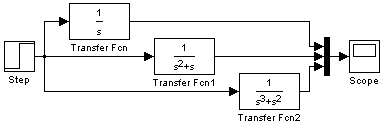
obr. 2.30 Blokově schéma programu Simulink - vykresleni h(t) pro integrační člen
sim_step_I.mdl - vykreslení prechodové charakteristiky integračních systémů (Simulink)
Podobně jako v předchozích případech porovnáme charakteristiky tří systémů tentokrát derivačních, které jsou zadány přenosy:
1. Derivační člen 1. řádu se setrvačností 1. řádu - ![]()
2. Derivační člen 1.řádu se setrvačností 2.řádu - ![]()
3. Derivační člen se setrvačností 2. řádu - ![]()
Stejně jako v předchozích případech použijeme pro zadání přenosu příkaz tf:
d=tf([3 0],[6 3]); d1=tf([3 0],[6 3 1]);d2=tf([3 1 0],[6 3 5 1]) |
a pro vykreslení grafů příkaz step:
step(d, d1, d2) |
Výsledný graf je na obr. 2.31.
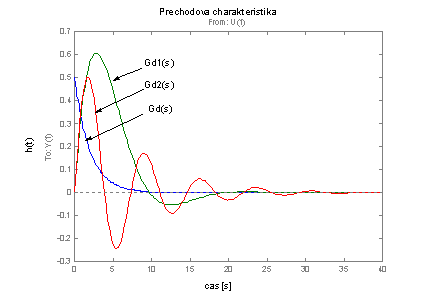
obr. 2.31 Vykreslení přechodových charakteristik derivačních systémů
vykr_step_D.m - vykreslení prechodové charakteristiky derivačních systémů
V programu Simulink provedeme zadání podle schématu na obr. 2.32.
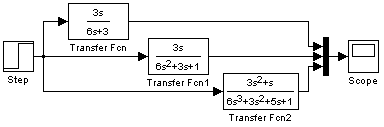
obr. 2.32 Blokové schéma programu Simulink - vykresleni h(t) pro derivační člen
sim_step_D.mdl - vykreslení prechodové charakteristiky derivačních systémů (Simulink)
Impulsní charakteristika g(t) je odezva systému na Diracův impuls na vstupu. Diracův nebo též jednotkový impuls se nedá fyzikálně realizovat. Při jeho realizaci se udává, že musí mít co největší amplitudu a nejkratší dobu trvání. Matematicky dosahuje Diracův impuls nenulové hodnoty pouze v čase t=0.[Švarc, I. 1992]
Více informací naleznete v publikaci: Prezentační a výukový modul pro oblast analýzy regulačních obvodů.
V programu Matlab můžeme impulsní charakteristiku zobrazit pomocí příkazu impulse, nebo pomocí příkazu ltiviews parametrem impulse. Vykreslení provedeme pomocí příkazů:
impulse(SYS) ltiview(‘impulse’,SYS) |
Podobně jako při vykreslení přechodové charakteristiky porovnáme charakteristiky tří proporcionálních systémů. Použijeme stejné přenosy, které zadáme pomocí funkce tf:
![]() ;
; ![]() ;
; ![]() ,
,
pro jejich zadání použijeme opět funkci tf:
p = tf(0.9, 1); p1 = tf([1], [3 1]); p2 = tf([5 1], [7 3 5]) |
Vykreslení pak provedeme pomocí příkazu impulse:
impulse(p,p1,p2) |
Výsledek podobě v grafu je na obr. 2.33.
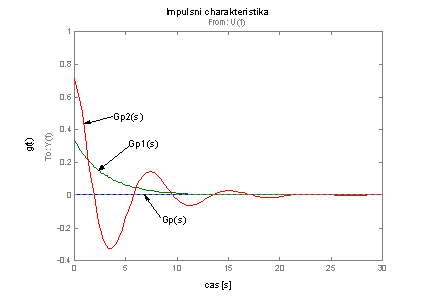
obr. 2.33 Impulsní charakteristiky proporcionálních systémů
vykr_imp_P.m - vykreslení impulsní charakteristiky proporcionálních systémů
Porovnání zadaných přenosů:
![]() ;
; ![]() ;
; ![]() .
.
Přenosy zadáme pomocí příkazu tf:
i = tf([1],[1 0]); i1 = tf([1], [1 1 0]); i2 = tf([1], [1 1 0 0]) |
Vykreslení pak provedeme pomocí příkazu impulse:
impulse(i,i1,i2) |
Výsledek podobě v grafu je na obr. 2.34.
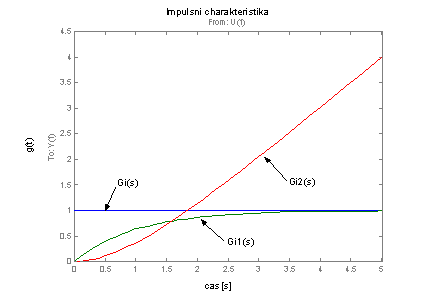
obr. 2.34 Impulsní charakteristiky integračních systémů
vykr_imp_I.m - vykreslení impulsní charakteristiky integračních systémů
![]() ;
; ![]() ;
; ![]() .
.
Stejně jako v předchozích případech použijeme pro zadání přenosu příkaz tf:
d=tf([3 0],[6 3]); d1=tf([3 0],[6 3 1]);d2=tf([3 1 0],[6 3 5 1]) |
Grafy vykreslíme funkcí impulse:
impulse(d, d1,d2) |
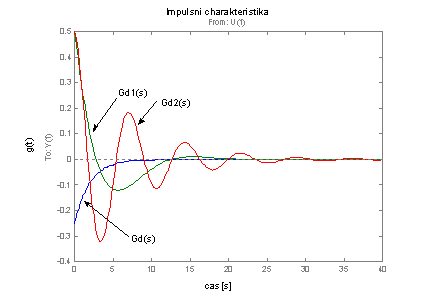
obr. 2.35 Impulsní charakteristiky derivačních systémů
vykr_imp_D.m - vykreslení impulsní charakteristiky derivačních systémů
Kmitočtový přenos je poměr výstupních a vstupních harmonických kmitů systému.
![]()
Základním vstupním signálem, kterého používáme při kmitočtovém vyšetřování vlastností lineárních systémů je sinusový průběh. Vzhledem k lineárnosti uvažovaného systému je výstupní signál také sinusový a mění se jen jeho amplitudová fáze. Je-li vstupní signál
![]()
je výstupní signál
![]() ,
,
kde u0, y0 jsou amplitudy vstupního a výstupního signálu, w úhlová frekvence a j fázové posunutí výstupního signálu vůči vstupnímu.
Kmitočtová charakteristika (obr. 2.36) je grafické znázornění G(jw) v komplexní (Gausově) rovině, přičemž proměnným parametrem je úhlová frekvence w, kterou měním od w=0 do w=¥. Při sestrojování kmitočtové charakteristiky si kmitočtový přenos G(jw) upravíme na složkový tvar komplexního čísla
![]() ,
,
kde vhodným hodnotám w počítáme reálnou a imaginární složku přenosu, které zakreslujeme do komplexní roviny.[Švarc, I. 1992]
Více informací naleznete v publikaci: Prezentační a výukový modul pro oblast analýzy regulačních obvodů.
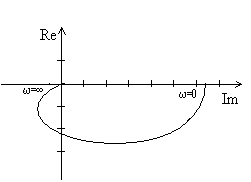
obr. 2.36 Frekvenční charakteristika v komplexní rovině
Pro vykreslení kmitočtové charakteristiky v programu Matlab můžeme použit příkaz nyquist, nebo příkaz ltiview s parametrem nyquist.
nyquist(SYS) ltiview(‘nyquist’,SYS) |
Kmitočtovou charakteristiku také někdy nazýváme amplitudo-fázovou charakteristikou v komplexní rovině. Teoreticky i prakticky se dá rozdělit na dvě charakteristiky – amplitudovou a fázovou. Pro větší přehlednost a jednoduchost tuto dvojici charakteristik vykreslujeme v logaritmických souřadnicích (obr. 2.38).
U obou charakteristik vynášíme hodnotu w na vodorovnou osu v logaritmickém měřítku jako logw. Tím dosáhneme velké rozmezí změn frekvence.
Na svislou osu amplitudové logaritmické charakteristiky vynášíme absolutní hodnotu kmitočtového přenosu, ale v jednotkách decibel. Decibel je v tomto případě definován jako dvacetinásobek dekadického logaritmu |G(jw)|
![]()
Hodnoty A[dB] vynášíme již v lineárním měřítku. Fázi vynášíme na svislou osu opět v lineárním měřítku.[Švarc, I. 1992]
Více informací naleznete v publikaci: Prezentační a výukový modul pro oblast analýzy regulačních obvodů.
Pro vykreslení logaritmické kmitočtové charakteristiky v programu Matlab můžeme použit příkaz bode, nebo příkaz ltiview s parametrem bode:
bode(SYS) ltiview(‘bode’,SYS) |
Opět použijeme přenosy z předchozích kapitol, které zadáme pomocí funkce tf:
![]() ;
; ![]() ;
; ![]()
p = tf(0.9, 1); p1 = tf([1], [3 1]); p2 = tf([5 1], [7 3 5]) |
Vykreslení kmitočtové charaktericky (obr. 2.37) pak provedeme pomocí příkazu nyquist:
nyquist(p, p1, p2) |
Logaritmicko kmitočtovou charakteristiku (obr. 2.38) vykreslíme pomocí funkce bode:
bode(p,p1,p2) |
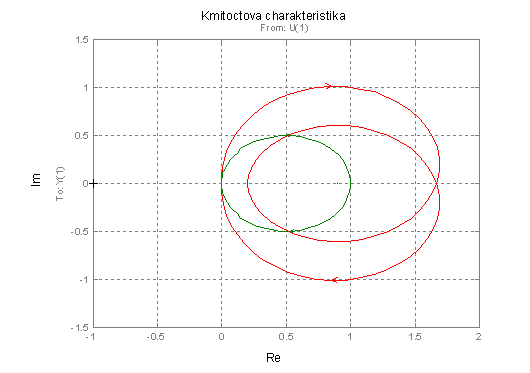
obr. 2.37 Kmitočtová charakteristika proporcionálních systémů
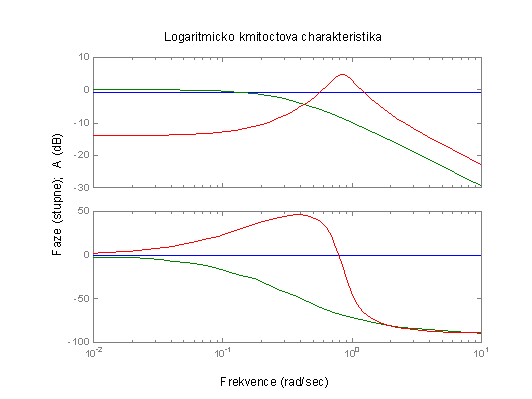
obr. 2.38 Logaritmická kmitočtová charakteristika proporcionálních systémů
vykr_kmit_P.m - vykreslení kmitočtové charakteristiky proporcionálních systémů
vykr_log_P.m - vykreslení logaritmické kmitočtové charakteristiky proporcionálních systémů
![]() ;
; ![]() ;
; ![]() .
.
Přenosy zadáme pomocí příkazu tf:
i = tf([1],[1 0]); i1 = tf([1], [1 1 0]); i2 = tf([1], [1 1 0 0]) |
Vykreslení kmitočtové charaktericky pak provedeme pomocí příkazu nyquist:
nyquist(i, i1, i2) |
Logaritmickou kmitočtovou charakteristiku vykreslíme pomocí funkce bode:
bode(i, i1, i2) |
vykr_kmit_I.m - vykreslení kmitočtové charakteristiky integračních systémů
vykr_log_I.m - vykreslení logaritmické kmitočtové charakteristiky integračních systémů
Pro porovnání máme opět zadány následující systémy:
![]() ;
; ![]() ;
; ![]() .
.
Stejně jako v předchozích případech použijeme pro zadání přenosu příkaz tf:
d=tf([3 0],[6 3]); d1=tf([3 0],[6 3 1]);d2=tf([3 1 0],[6 3 5 1]) |
Vykreslení frekvenční charaktericky pak provedeme pomocí příkazu nyquist:
nyquist(i, i1, i2) |
Logaritmicko frekvenční charakteristiku vykreslíme pomocí funkce bode:
bode(i, i1, i2) |
vykr_kmit_D.m - vykreslení kmitočtové charakteristiky derivačních systémů
vykr_log_D.m - vykreslení logaritmické kmitočtové charakteristiky derivačních systémů systémů