(8.1)
8.1.1 Definice stability a obecné podmínky stability
Stabilita je jedním ze základních požadavků, které klademe na regulační obvod. Regulační obvod je stabilní, jestliže pro vychýlení regulačního obvodu z rovnovážného stavu a odeznění vnějších sil, které tuto odchylku způsobily, se regulační obvod během času znovu vrátí do původního rovnovážného stavu. Jinak řečeno je stabilita vlastnost regulačního obvodu udržet se v okolí rovnovážného stavu nebo se do něj vrátit po odeznění vnějších působících sil. Matematicky lze stabilitu definovat
|
(8.1) |
Z hlediska stability rozlišujeme RO stabilní, na mezi stability a nestabilní (viz obr. 8.1). RO na mezi stability se považují za stabilní. Vždy se vyžaduje, aby regulační obvod byl za všech okolností stabilní. Zatímco parametry a dynamické vlastnosti regulované soustavy jsou dány konstrukcí soustavy, technologickým procesem apod. a nemůžeme je tudíž měnit, můžeme měnit dynamické vlastnosti regulátoru nastavováním volitelných parametrů regulátoru. Tím můžeme dosáhnout stability (a dalších vlastností) regulačního obvodu.
a)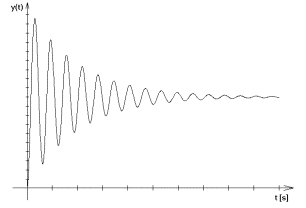
c)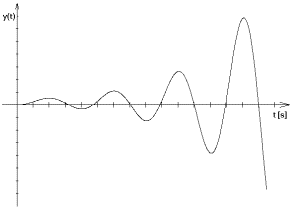
a) stabilní, b) mez stability, c) nestabilní
obr. 8.1. Příklady průběhů regulačního pochodu
Při vyšetřování stability se vychází z tzv. charakteristického mnohočlenu, který je ve jmenovateli všech základní přenosů RO (4.1-4). Má-li charakteristická rovnice (4.8) pouze nenásobené reálné kořeny si, je řešení rovnice (6.26) [při uvažování u(t) = 0]- tedy hledaný přechodný děj - ve tvaru
|
(8.2) |
kde ci jsou konstanty vypočtené z počátečních podmínek.
Jestliže má charakteristická rovnice (4.8) dvojici komplexně sdružených kořenů, sk = a + jb, sk+1 = a - jb, bude řešení rovnice (6.26) mít tvar
|
(8.3) |
Ze vztahů (8.1), (8.2), (8.3) vyplývá nutná a postačující podmínka stability RO, která se týká kořenů charakteristické rovnice (4.8). Regulační obvod je stabilní právě tehdy, když všechny kořeny charakteristické rovnice mají záporné reálné části, tedy leží-li v levé komplexní polorovině, viz obr. 8.2, [Švarc, I 1992, Hanuš,B.,Balda, M. & kolektiv 1989]
|
(8.4) |
obr. 8.2. Oblast stability spojitých RO
Kontrola stability RO spočívá v určení rozložení kořenů charakteristické rovnice v komplexní rovině kořenů. Pokud lze kořeny vyčíslit, použijeme nutnou a postačující podmínku stability. Jinak je nutno použít pravidla, která umožní rozhodnout o stabilitě bez přímého výpočtu kořenů, tyto pravidla se nazývají kritéria stability. V následujících odstavcích jsou uvedeny kritéria, která se často používají.