3.2 LKCH základních zapojení

Sériové zapojení

Celkový přenos lineárních dynamických členů zapojených sériově (obr. 2.4) je dán součinem přenosů jednotlivých členů, viz vztah (2.3). Amplituda a fáze výsledného přenosu se vypočte

,

(3.9)

.

(3.10)

Z výše uvedených vztahů vyplývá, že výsledná LKCH je dána součtem LKCH jednotlivých členů zapojených sériově (obr. 3.1).

obr. 3.1. LKCH sériově zapojených členů

Paralelní zapojení

Celkový přenos lineárních dynamických členů zapojených paralelně (obr. 2.5) je dán součtem, resp. rozdílem přenosů jednotlivých členů, viz vztah (2.6). Také kmitočtový přenos je dán součtem, resp. rozdílem kmitočtových přenosů jednotlivých členů. Pokud v obvodu budou zařazeny jen členy s minimální fází (existuje jednoznačné přiřazení mezi LAKCH a LFKCH), stačí jen sestrojit LAKCH a LFKCH bude sestrojena na základě výsledné LAKCH.

Pro konstrukci LAKCH paralelně zapojených členů se uvažuje přibližný kmitočtový přenos

,

(3.11)

kde A₁(w), A₂(w) jsou moduly dílčích členů. Pak přibližná výsledná LAKCH je rovna vždy LAKCH členu s větší amplitudou.

.

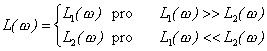(3.12)

obr. 3.2. LKCH paralelního zapojení

Zpětnovazební zapojení

Rovněž u tohoto zapojení (obr. 2.6) lze sestrojit přibližné LAKCH, za předpokladu, že v obvodu jsou jen dynamické členy s minimální fázi. Přibližný kmitočtový přenos je popsán rovnicí

.

(3.13)

Přibližná výsledná LAKCH zpětnovazebního obvodu je rovna

.

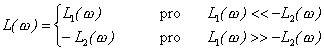(3.14)

Příklad sestrojení LKCH je na obr. 3.3.

obr. 3.3. LKCH zpětnovazebního zapojení

Inverzní člen

Pokud známe LKCH členu o přenosu G₁(s), pak můžeme snadno sestrojit charakteristiku členu s inverzními dynamickými vlastnostmi, tj. s přenosem

.

(3.15)

Kmitočtový přenos má tvar

.

(3.16)

pak amplituda a fáze je dána vztahy

.

(3.17)

.

(3.18)

LKCH členů s inverzními vlastnostmi se liší jen znaménkem, tvar mají stejný, viz. obr. 3.4.

obr. 3.4. LKCH členů s inverzními vlastnostmi

Zpět na začátek