Rozlišujeme sériové, paralelní a zpětnovazební (antiparalelní) zapojení.
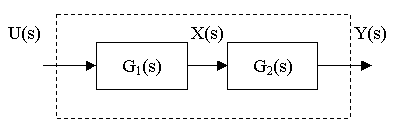
Sériové zapojení - obr. 2.4.
obr. 2.4 Blokové schéma sériového zapojení
Pro jednotlivé členy platí vztahy:
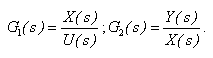 |
(2.1) |
Vztah pro výstupní veličinu odvodíme eliminací proměnné X(s)
|
(2.2) |
Je tedy možno sériově zapojené členy nahradit jedním členem s přenosem
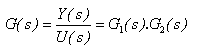 |
(2.3) |
Při sériovém zapojení členů je výsledný přenos dán součinem přenosů jednotlivých členů.
Paralelní zapojení - obr. 2.5.
obr. 2.5. Blokové schéma paralelního zapojení
Pro jednotlivé členy a pro součtový uzel platí vztahy:
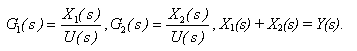 |
(2.4) |
Eliminací X1(s), X2(s) vypočítáme výstupní veličinu Y(s)
|
(2.5) |
Při paralelním zapojení členů je možné je nahradit jedním členem s přenosem
|
(2.6) |
Při paralelním zapojení je výsledný přenos dán součtem (respektive rozdílem) přenosů jednotlivých členů.
Zpětnovazební zapojení (antiparalelní) - obr. 2.6.
obr. 2.6. Blokové schéma zpětnovazebního zapojení
Pro jednotlivé členy a rozdílový uzel platí vztahy:
|
(2.7) |
Eliminací X(s) a Y1(s) obdržíme vztah pro výstupní veličinu Y(s)
|
(2.8) |
|
(2.9) |
Při zpětnovazebním zapojení se zápornou zpětnou vazbou je možno takto zapojené členy nahradit jedním členem s přenosem
|
(2.10) |
Při zpětnovazebním zapojení je výsledný přenos dán zlomkem, kdy v čitateli je tzv. přenos přímé větve a ve jmenovateli 1± součin přenosů přímé větve a zpětné vazby:
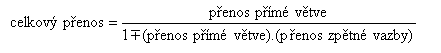
Znalost blokové algebry umožňuje zjednodušovat složitá bloková schémata a stanovit výsledný přenos zapojení. Zjednodušovat je nejlépe tak, že uvnitř blokového schématu hledáme některé z uvedených základních zapojení a postupně nahrazujeme tato zapojení jediným členem.[Švarc, I. 1992]