Příklad 3.8
Máme za úkol pomocí metody PERT určit očekávaný termín
realizace úkolu, jeho směrodatnou odchylku a očekávané celkové časové rezervy.
Naším dalším úkolem bude určit pravděpodobnost dodržení plánovaného termínu TP =
Tabulka 3.7 Zadání k příkladu 3.8
|
činnost |
i |
j |
a |
m |
b |
te |
|
omezení |
|
|
A |
1 |
2 |
2 |
3 |
4 |
3 |
0,11 |
A < B, C |
0 |
|
B |
2 |
3 |
5 |
11 |
11 |
10 |
1 |
B < E, F |
0 |
|
C |
2 |
4 |
2 |
2 |
2 |
2 |
0 |
C < F |
8 |
|
D |
3 |
4 |
0 |
0 |
0 |
0 |
0 |
|
0 |
|
E |
3 |
5 |
3 |
5 |
13 |
6 |
2,78 |
E < G |
2 |
|
F |
4 |
5 |
2 |
9 |
10 |
8 |
1,78 |
F < G |
0 |
|
G |
5 |
6 |
1 |
5 |
15 |
6 |
5,44 |
|
0 |
Řešení:
Doby te v tabulce 3.7 byly dopočteny pomocí vztahu
![]()
a hodnoty ![]() pomocí vzorce:
pomocí vzorce:
![]()
V uzlech jsou rozmístěny hodnoty takto
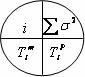
Obr. 3.32 Označení v uzlu u metody PERT
kde i je číslo uzlu
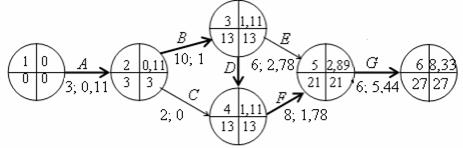
Obr. 3.33 Výsledný síťový graf - příklad 3.8
Z grafu odečteme hodnoty pro realizaci celého úkolu:
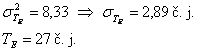
Pravděpodobnost dodržení plánovaného termínu TP = 24 č.j. (viz tab. 2.7):
![]()
Pravděpodobnost dodržení plánovaného termínu TP = 30 č.j. (viz tab. 2.7):
![]()
Očekávané celkové časové rezervy pro jednotlivé činnosti jsou uvedeny v tabulce 3.7. Pravděpodobnost dodržení plánovaného termínu TP(24) = 15 % a TP(30) = 85 %. Výsledný síťový graf je uveden na obr. 3.33.