Jde o metodu založenou na analytickém nebo experimentálním určování kritického zesílení. Po zjištění kritického zesílení provedeme výpočet koeficientů spojitého i diskrétního regulátoru nazákladě tabulky 3.1.
Metodu můžeme přímo v programu Matlab kombinovat s graficko-analytickým postupem, při kterém zjistíme nejdříve kritickou frekvenci a kritické zesílení na základě příkazů bode (logaritmická frekvenční charakteristika) a margin (kritická hodnota zesílení a kritická hodnota frekvence), a potom z těchto hodnot určím koeficienty regulátoru podle tabulky 3.1[Dušek F. 2000].
tab. 3.1 Nastavení koeficientů metodou Zieglera - Nicholse
| Typ regulátoru |
Proporcionální složka kp |
Integrační složka TI |
Derivační složka TD |
|
P |
0,50kkrit |
- |
- |
|
PI |
0,45kkrit |
0,85Tkrit |
- |
|
PD |
0,40kkrit |
- |
0,50Tkrit |
|
PID |
0,60kkrit |
0,50Tkrit |
0,12Tkrit |
|
Kkrit – kritické zesílení; Tkrit – kritická perioda (Tkrit=2*p/wkrit) |
|||
Více informací naleznete v publikaci: Syntéza regulačních obvodů.
Vypočítejte koeficienty spojitého PID regulátoru pro soustavu zadanou přenosem:
![]()
Řešení:
Nejdříve zadáme přenos systému:
sys=tf(9,[1 6 9 0])
Transfer function:
9
-----------------
s^3 + 6 s^2 + 9 s |
Pomocí příkazu margin určíme hodnoty kritického zesílení a kritické frekvence.
[Kr,Fk,wk,wf]=margin(sys) |
Získali jsme následující hodnoty:
Kr = 6 % kritická hodnota zesílení Fk = 56.0798 % kritická fáze wk =3 % kritické frekvence pro kritické zesílení wf = 0.9149 % kritické frekvence pro kritickou fázi |
Tyto hodnoty můžeme zobrazit i graficky pomocí příkazu:
margin(sys) |
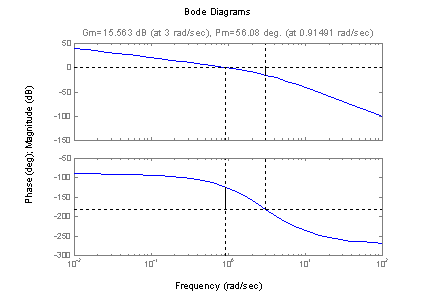
obr. 3.1 Logaritmická frekvenční charakteristika soustavy s vyznačením kritických hodnot
V dalším kroku vypočítáme kritickou periodu Tk.
Tk=2*pi/wk |
Nyní již známe obě potřebné hodnoty (kritické zesílení a perioda) pro výpočet parametrů regulátoru:
K=0.6*Kr % vypocet zesileni PID regulatoru Ti=0.5*Tk % vypocet integracni casove konstanty Td=0.12*Tk % vypocet derivacni casove konstanty |
Z vypočítaných hodnot k, TI, TD sestavíme přenos regulátoru:
reg = tf([K*Ti*Td K*Ti K],[Ti 0]) % prenos PID regulatoru
Transfer function:
0.9475 s^2 + 3.77 s + 3.6
-------------------------
1.047 s |
Posledním krokem je propojení soustavy a regulátoru do uzavřeného regulačního obvodu k tomu můžeme použít příkaz feedback pro zpětnovazební propojení.
Go=sys*reg %prenos otevreneho regulacniho obvodu
Gro=feedback(Go,1) %prenos uzavreneho regulacniho obvodu
Transfer function:
8.527 s^2 + 33.93 s + 32.4
--------------------------------------------------
1.047 s^4 + 6.283 s^3 + 17.95 s^2 + 33.93 s + 32.4 |
Přechodová charakteristika uzavřeného regulačního obvodu je na obr. 3.2.
step(Gro) |
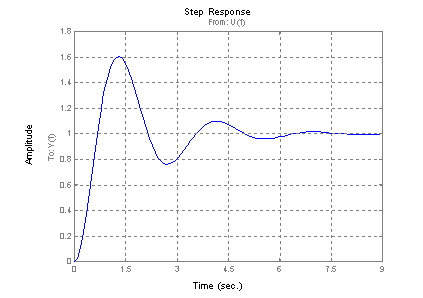
obr. 3.2 Přechodová charakteristika uzavřeného regulačního obvodu
reg_ZN.m - řešení v m-file