Popis systému v oblasti komplexní proměnné s.
Přenos systému definujeme jako poměr Laplaceova obrazu výstupní veličiny k Laplaceovu obrazu vstupní veličiny při nulových počátečních podmínkách. Značíme ho symbolem G(s) a za předpokladu, že L{u(t)}=U(s) a L{y(t)}=Y(s) můžeme jeho definici psát ve tvaru
| (2.12) |
Máme-li systém, popsaný diferenciální rovnicí (2.1), provedeme transformaci této rovnice za použití věty o linearitě a věty o obrazu n-té derivace v Laplaceově transformaci. Jestliže podle definice přenosu položíme všechny počáteční podmínky rovny nule, dostaneme po vytknutí na levé i pravé straně vztah
odtud podle definice (2.12) vyplyne vzorec pro výpočet přenosu z koeficientů známé diferenciální rovnice
| (2.13) |
Tento vzorec má oproti definici v čitateli polynom, vytvořený ze vstupní strany diferenciální rovnice a ve jmenovateli polynom z výstupní strany diferenciální rovnice. [Švarc, I. 1992]
Více informací naleznete v publikaci: Prezentační a výukový modul pro oblast analýzy regulačních obvodů.
Systém Matlab nám diky toolboxu Control System poskytuje několik možností zadání přenosu.
Základní syntaxe příkazu:
SYS = TF(NUM,DEN) - spojitý systém zadáváme čitatele a jmenovatele
sys = tf(NUM, DEN,'OutputDelay',Td) - pokud potřebujeme zadat dopravní zpoždění přidáme parametr OutputDelay a hodnotu zpoždění Td.
s = TF('s') - vytvoření komplexní proměnné s
Máme systém zadaný přenosem:
Pro zadání přenosu použijeme příkaz:
sys = tf([1.2 0.5], [7.1 2 1.5 0.1]) |
Do proměnné sys se uložil přenos v tomto tvaru:
Transfer function:
1.2 s + 0.5
-----------------------------
7.1 s^3 + 2 s^2 + 1.5 s + 0.1
|
Při zadávání přenosu můžeme nejdřív zadat do vlastních proměnných koeficienty čitatele a jmenovatele a teprve potom pomocí těchto proměnných zadat přenos:
cit = [1.2 0.5];
jmen = [7.1 2 1.5 0.1];
sys = tf(cit, jmen)
Transfer function:
1.2s + 0.5
-----------------------------
7.1 s^3 + 2 s^2 + 1.5 s + 0.1 |
Přenos můžeme zadat také tak, že si nejdříve vytvoříme komplexní proměnnou s:
s = tf('s') |
Přenos pak zadáme následujícím způsobem:
sys=(1.2*s+0.5)/(7.1*s^3+2*s^2+1.5*s+0.1)
Transfer function:
1.2 s + 0.5
-----------------------------
7.1 s^3 + 2 s^2 + 1.5 s + 0.1 |
prenos.m - příklad zadání spojitého a diskrétního přenosu pomocí funkce tf (m-file)
Zadání diskrétního systému je obdobné jako u systému spojitého. Navíc zde zadáváme vzorkovací periodu Ts ( vzorkovací perioda je častěji označována T v matlabu jer však použito značení Ts ).
Základní syntaxe příkazu:
SYS = TF(NUM,DEN,Ts) - zadáváme čitatele jmenovatele a vzorkovací periodu
z = TF('z',Ts) - vytvoření diskrétní proměnné z
Máme systém zadaný přenosem:
Pro zadání přenosu použijeme příkaz:
sys = tf([1.2 0.5], [7.1 2 1.5 0.1], 0.1) |
Do proměnné sys se uložil přenos v tomto tvaru:
Transfer function:
1.2 z + 0.5
-----------------------------
7.1 z^3 + 2 z^2 + 1.5 z + 0.1
Sampling time: 0.1 |
prenos.m - příklad zadání spojitého a diskrétního přenosu pomocí funkce tf (m-file)
Funkce tf je v programu Simulink zprostředkována pomocí bloků Transfer Fnc pro spojité systémy a Disckrete Transfer Fnc pro diskrétní systémy viz. obr. 2.11 .
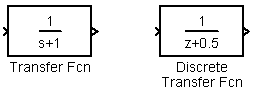
2.11 Bloky tf programu Simulink
Na obrázku obr. 2.12 je příklad zapojení bloku Transfer Fnc pro vykreslení přechodové charakteristiky spojitého systému.

obr. 2.12 Blokové schéma pro vykreslení přechodové charakteristiky pomocí bloku Transfer Fnc
sim_tf.mdl - zapojení bloků Transfer Fnc a Discrete Transfer Fnc v programu Simulink.