Dynamické vlastnostisystému lze popsat různýmizpůsoby, které lze v podstatě rozdělit do dvou skupin a to na vnitřní a vnější popis systému.
Vnější popis systému je vyjádření dynamických vlastností systému závislostí mezijeho vstupem a výstupem. Přivnějším popisu systému považujeme systém za černou skříňku se vstupem a výstupem.
Vnějších popisů lineárního systému je několik. Všechny systém jednoznačně charakterizují a povětšině lze z jednoho druhu popisu odvodit další.
Pod pojmem popis lineárního regulačního systému sinejčastějipředstavíme popis řízeného systému (regulované soustavy). Tomu napovídá ipoužívané označení u(t) pro vstupní veličinu a y(t) pro výstupní veličinu. Ale můžeme tím myslet ipopis prvků systému. Rovněž tak můžeme stejným způsobem popisovat iřídící systém, kde je opačné značení vstupní a výstupní veličiny.
Vnější popis lineárního spojitého systému s jednou vstupní a jednou výstupní veličinou může být:
Jediným vnitřním popisem systému je jeho popis ve stavovém prostoru tzv. stavový popis. Vnitřní popis systému je vyjádření dynamických vlastností systému závislostí mezijeho vstupem, stavem a výstupem.
Vnitřní popis systému je popis jeho stavově přechodné struktury Je nejdokonalejším popisem systému. Vyjadřujeme jej pomocí stavových rovnic.
Více informací naleznete v publikaci: Prezentační a výukový modul pro oblast analýzy regulačních obvodů.
Jede o popis systému v časové oblasti.
Lineární spojitý systém S s jednou vstupní a jednou výstupní veličinou podle obr. 2.1 má obecnou závislost mezivstupem a výstupem popsán rovnicí ve tvaru
| (2.1) |
kde
ai, bi jsou koeficienty levé a pravé strany diferenciální rovnice,
u(t) je vstupní veličina,
y(t) výstupní veličina.
obr. 2.1 Blokové schéma systému
Diferenciální rovnicisystému získáme obvykle tak, že uvedeme fyzikální vztahy systému a eliminujeme všechny proměnné mimo vstupní a výstupní veličinu. Např. v mechanických systémech obvykle vystačíme s dynamickou rovnováhou sil [Švarc, I. 1992].
Matlab umožňuje diferenciální rovnice řešit numericky. Pro zadání diferenciální rovnice do programu Matlab máme dvě možnosti. Rovnicimůžeme zadat pomocí toolboxu Simulink, kde sestavíme její blokové schéma. Druhou možností je naprogramovat sipomocí m-file editoru vlastní funkci, do které zadáme parametry rovnice.
Provedeme analytickou identifikacinádrže s volným odtokem kapaliny obr. 2.2 za předpokladu, že h(t) je výška hladiny [m], P je obsah příčného průřezu hladiny [m2], A je obsah příčného průřezu odtoku [m2], q1 je objemový přítok [m3s-1], q2 je objemový odtok [m3s-1] a j rychlostní součinitel.
Pro q2 platí:
| (2.2) |
Máme zadány následující hodnoty:
P = 2 m2
q1 = 0,1 m3s-1
A = 0,1 m2
j
= 0,9
h(0) = 0,1 m
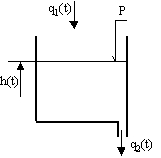
obr.2.2 Nádrž s volným odtokem
Pro elementární přírůstek objemu kapaliny v nádržiPdh(t) za elementární časový přírůstek dt platí rovnice
Pdh(t) = q1(t)dt – q2(t)dt,
Resp. Po uvažování vztahu (2.2)
Pdh(t) = q1(t)dt - ![]()
Po úpravě dostaneme nelineární nehomogenní diferenciální rovnici1. řádu
| (2.3) |
a) Řešení pomocí toolboxu Simulink
Na obr. 2.3 je vidět blokové schéma diferenciální rovnice vytvořené v toolboxu Simulink, přisestavení blokového schéma vycházíme z rovnice (2.3).

obr. 2.3 Řešení diferenciální rovnice nádrže v programu Simulink
Popis jednotlivých bloků a jejich nastavení:
Step – skoková změna pro nás představuje přítok nádrže q1. Zde nastavíme tyto parametry:
Step time – zde uvádíme v jakém čase od začátku simulace dojde k zapnutí skokové změny čas uvádíme v sekundách. Hodnotu nastavíme na nulu.
Initial value – počáteční hodnota. Hodnotu nastavíme na nulu.
Final value – výsledná hodnota skoku kterou nastavíme na hodnotu 0,1.
Gain – zesílení tento blok vynásobí vstupní signál požadovanou hodnotou. V tomto řešení je zesílení použito dvakrát:
Gain – Zde je zadána hodnota 1 / P ve tvaru 1 / 2.
Gain2 – V tomto zesílení je zadán vztah ![]() ve tvaru 0.1*0.9*sqrt(2*9.81).
ve tvaru 0.1*0.9*sqrt(2*9.81).
Integrátor – Integrační člen v tomto členu zadáváme počáteční podmínku 0,1.
Math Function – tento blok umožňuje provedené několika matematických funkci. Pro nás je důležitá funkce odmocnina – sqrt.
Scope – nástroj na zobrazení výsledného signálu v závislosti na čase. Graf otevřeme poklepáním na tento blok.
sim_nadrz.mdl - řešení diferenciální rovnice v programu Simulink
b) Řešení pomocí m-file
Zadání funkce:
function hp = difrov (t, h) % deklarace funkce a načtení hodnot:
% t-doba simulace,
% h-počáteční podmínka
q1 = 0.1; %zadání konstant
A = 0.1; %zadání konstant
fi= 0.9; %zadání konstant
g = 9.81; %zadání konstant
hp = (q1 - A*fi*sqrt(2*g*h))/2; %zadání diferencialní rovnice
|
Název uloženého souboru se musí shodovat s názvem funkce. V tomto případě se soubor bude jmenovat difrov.m. Přivolbě názvu funkce nesmíme zapomenout, že naše funkce nesmí mít stejný název jako vestavěné funkce programu Matlab.
Abychom mohli vytvořenou funkciv podobě m-file v spustit musíme v programu nastavit cestu do adresáře kde je náš soubor uložen. Matlab standardně nabízí složku MATLABR11\work. Nastavení cesty ke složce můžeme změnit pomocí nástroje Path Browser (File - SetPath…), pomocí tohoto nástroje také můžeme cestu k našemu adresáři uložit pro příští spuštění.
Výpočet:
[t,y]=ode45('difrov',[0:0.1:30], 0.1); %volaní funkce difrov a výpočet
|
Funkce ode45 je numerická funkce řešení diferenciálních rovnic. Parametry [t, y] určují jména proměnných, kde bude uložen výsledek. Parametr 'difrov' volá našivytvořenou funkci. Hodnoty [0:0.1:30] určují krok a dobu řešení. Poslední uvedená hodnota 0,1 je počáteční podmínka y0.
plot (t, y); %vykreslení grafu
grid; %zapnutí zobrazení mřížky
title ('Výška hladiny v nádrži'); %titulek grafu
xlabel ('doba simulace'); %popis osy x
ylabel ('výška hladiny'); %popis osy y
|
Výsledek:
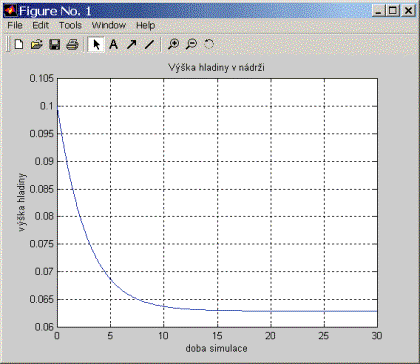
obr.2.4 Vykreslení přechodové charakteristiky modelu nádrže
nadrzdif.m - zadání funkce
nadrz.m - řešení a vykreslení diferenciální rovnice
Provedeme analytickou identifikacielektrického obvodu se dvěma prvky kondenzátorem C a odporem R a vstupním napětím u1. Zapojení obvodu je patrné z obr. 2.5 .
Máme zadány hodnoty:
R = 10 kW
C = 10 mF
u1 = 220V
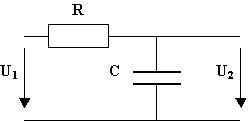
obr. 2.5 Zapojení RC členu
Při řešení elektrických obvodů vycházíme z Ohmova zákona a Kirchhoffových zákonů.
Pro úbytek napětí na odporu R platí vztah
| (2.4) |
pro úbytek napětí na kondenzátoru C platí:
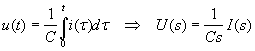 . . |
(2.5) |
Poměr výstupního napětí na vstupním je možné popsat vztahem
|
(2.6) |
kde Z1(s) představuje příčnou větev obvodu (kondenzátor C) a Z2(s) horní větev obvodu (odpor R).
Dosazením vztahů (2.4) a (2.5) do rovnice (2.6) získáme
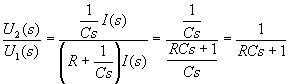 .
.
Výsledkem je rovnice vyjadřující závislost výstupního napětí u2 na vstupním napětí u1 ve tvaru
![]() ,
,
tuto rovnici upravíme na následující tvar
![]() .
.
Pomocí zpětné Laplaceovy transformace rovnicipřevedeme z oblastikomplexní proměnné s do časové oblastia vyjádříme nejvyšší derivaci:
| (2.7) |
a) Řešení pomocí toolboxu Simulink
Na obr. 2.6 je vidět blokové schéma diferenciální rovnice vytvořené v toolboxu Simulink při sestavení blokového schéma vycházíme z rovnice (2.7).
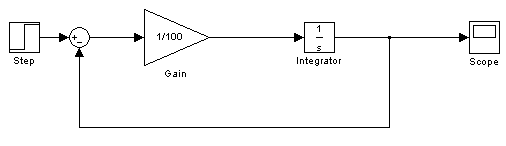
obr.2.6 Řešení diferenciální rovnice RC členu v programu Simulink
Popis jednotlivých bloků a jejich nastavení:
Step – zde nastavíme vstupní napětí u1: Step time = 0, Final value = 220.
Gain – do zesílení nastavíme hodnotu 1/RC.
Integrátor – Integrační člen v tomto členu zadáváme počáteční podmínku 0.
Scope – nástroj na zobrazení výsledného signálu v závislostina čase. Graf otevřeme poklepáním na tento blok.
sim_RCclen.mdl - řešení diferenciální rovnice v programu Simulink
b) Řešení pomocí m-file
Zadání funkce:
function u2 = difrov2 (t, u) % deklarace funkce a načtení hodnot:
% t-doba simulace,
% u-počáteční podmínka u2
u1=220; %zadání konstant
R=10000; %zadání konstant
C=0.01; %zadání konstant
RC=R*C; %zadání konstant
u2= (u1 - u)/RC; %diferencialní rovnice
|
Výpočet:
[t,u]=ode45('difrov2', [0:0.1:800], [0]); % volání funkce difrov2
|
Funkce ode45 je numerická funkce řešení diferenciálních rovnic. Parametry [t, u] určují jména proměnných, kde bude uložen výsledek. Parametr 'difrov2' volá našivytvořenou funkci. Hodnoty [0:0.1:800] určují krok a dobu řešení. Poslední uvedená hodnota 0 je počáteční podmínka.
Vykreslení:
plot (t, u); %vykreslení grafu
grid; %zobrazení mřížky
title ('průběh napětí u2'); %titulek grafu
xlabel ('doba simulace'); %popis osy x
ylabel ('napětí') % popis osy y
|
Výsledek:
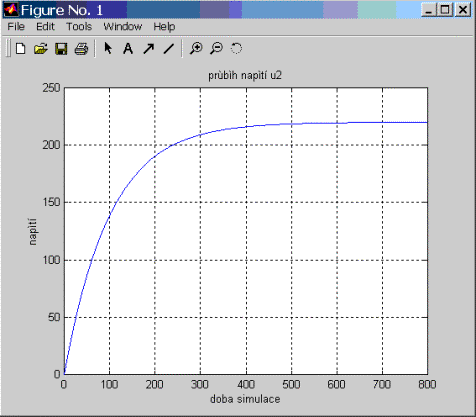
obr.2.7 Vykreslení přechodové charakteristiky modelu RC členu
RCdif.m - zadaní funkce
RC.m - řešení a vykreslení diferenciální rovnice
Provedeme analytickou identifikacisystému s hmotou na pružině a tlumiči (obr. 2.8) za předpokladu, že k – tuhost pružiny [kg.s-2], b – odpor tlumiče [kg.s-1], m – hmotnost [kg] a F – působící vstupní síla [N]. Sledované výstupní veličiny jsou y(t) – průběh rychlostihmoty [m.s-1] a y(t) – průběh výchylky polohy hmoty [m].
Máme zadány hodnoty: F = 50N
m = 2kg
k = 5kg.s-2
b = 0,5kg.s-1
y0 = 5m
y’0 = 0m.s-1
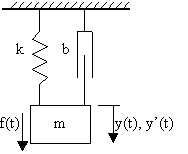
obr. 2.8 Hmota na pružině a tlumiči
Přiřešení vycházíme z pohybové rovnice
pro náš příklad má pohybová rovnice následující tvar
| (2.8) |
Jednotlivé síly spočítáme podle následujících vztahů
Po dosazení do rovnice (2.8) získáme diferenciální rovnici druhého řádu
po úpravě získáme tvar
| (2.9) |
a) Řešení pomocí toolboxu Simulink
Na obr. 2.9 je vidět blokové schéma diferenciální rovnice vytvořené v toolboxu Simulink přisestavení blokového schéma vycházíme z rovnice (2.9).
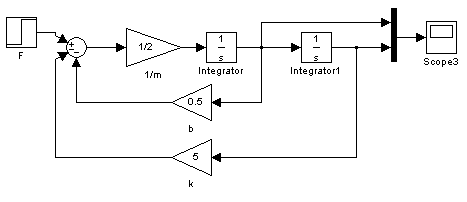
obr.2.9 Řešení diferenciální rovnice hmoty na pružině a tlumiči v programu Simulink
Popis jednotlivých bloků a jejich nastavení:
Step – zde natavíme vstupní sílu F: Step time = 0, Final value = 50.
Gain – hodnoty jednotlivých zesílení jsou patrné z obr. 2.9
Integrátor – Integrátor nastavíme na hodnotu 0, Integrátor1 na hodnotu 5
sim_hmota.mdl - řešení diferencilánírovnice v programu Simulink
b) Řešení pomocí m-file
Protože numericky je možné řešit pouze diferenciální rovnice prvního řádu, musíme nejdříve výchozí diferenciální rovnici druhého řádu (2.9) převést na soustavu diferenciálních rovnic prvního řádu.
Nejdříve zavedeme substituci
y1= y; y2 = y’,
po zavedení substituce získáme soustavu dvou diferenciálních rovnic prvního řádu
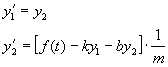 . . |
(2.10) |
Ze soustavy rovnic (2.10) získáme vektorový popis
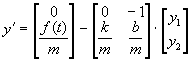 |
(2.11) |
Zadání funkce:
function yp = difrov1 (t, y) % deklarace funkce a načtení hodnot:
% t-doba simulace
% y-počáteční podmínky
f = [0;25]; % zadání konstant - Vektoru f
k = [0 -1;2.5 0.25]; %zadání konstant - Vektoru K (hodnoty k, b)
yp = f-k*y; %zadání diferenciální rovnice podle vztahu
|
Přizadávání konstant a diferenciální rovnice vycházíme ze vztahu (2.11) proto f a k zadáváme jako matice. Výsledná hodnota bude také matice yp, kde první sloupec bude obsahovat hodnoty y’1 a druhý sloupec hodnoty y’2.
Název uloženého souboru se musí shodovat s názvem funkce. V tomto případě se soubor bude jmenovat difrov1.m.
Výpočet
[t,yp]=ode45('difrov1', [0:0.1:50], [5;0]);
|
Funkce ode45 je numerická funkce řešení diferenciálních rovnic. Parametry [t, yp] určují jména proměnných, kde bude uložen výsledek. V proměnné yp bude uložen jako matice. Parametr 'difrov1' volá naši vytvořenou funkci. Hodnoty [0:0.1:30] určují krok a dobu řešení. Poslední hodnota [5;0] je matice počátečních podmínek.
Vykreslení:
plot (t, yp) %vykresleni grafu
grid; %zobrazeni mřížky
title ('průběh výchylky a rychlosti hmoty'); %titulek grafu
xlabel ('doba simulace'); %popis osy x
ylabel ('výchylka, rychlost'); %popis osy y
|
Výsledek:
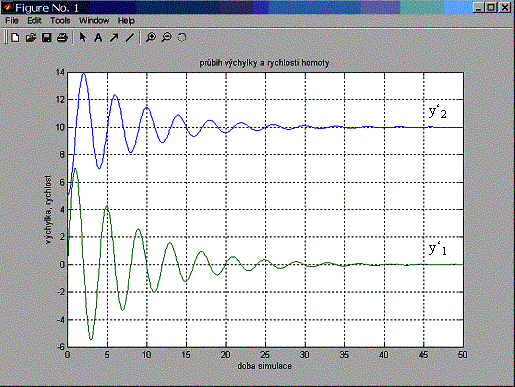
obr.2.10 Vykreslení přechodové charakteristiky modelu hmoty na pružině a tlumiči
hmotadif.m - zadání funkce
hmota.m - řešení a vykreslení diferenciální rovnice