4. Ekologické systémy

Poznatky, získané při studiu předchozích kapitol, popisujících především příklady z technické praxe, můžeme využít v řadě dalších disciplín. Ukažme si to alespoň na jedné oblasti, která se v poslední době značně rozvíjí, a to na simulaci ekologických systémů (ekosystémů).
V této kapitole budou postupně představeny matematické modely různých ekologických systémů a simulace jejich chování na číslicovém počítači [1, 9, 12]. Nejjednodušším modelem, který uvedeme, je simulace chování výšky hladiny ledovcového jezera v závislosti na přítoku vody. Na příkladu věnovaném růstu populace baktérií ukážeme postup při návrhu nejjednoduššího modelu systému a jeho následné zdokonalování. Přitom předpokládáme, že baktérie mají neomezený přísun živin. Systém tedy nebude obsahovat žádnou vstupní veličinu, výstupní veličinou bude počet baktérií v populaci, označíme ji y(t).

4.1. Ledovcové jezero

Vyšetřujeme ledovcové jezero bez přirozeného odtoku. Definovali jsme systém, jehož vstupní veličina u(t) je přítok vody do jezera [m³s^-1] a výstupní veličina y(t) je výška hladiny v jezeře [m]. Provedeme identifikaci závislosti výšky hladiny jezera na přítoku. Při identifikaci provedeme několik zjednodušení. Vždy se budeme snažit postihnout hlavní vlivy na chování systému a potlačit vlivy podružné. Tím značně zjednodušíme postup práce.

Matematický model ledovcového jezera

Při stanovení zákonitosti v chování jezera využijeme platnosti zákona o zachování hmoty. Za krátký časový úsek (označíme ho t) přiteče do jezera množství vody rovné t.u(t) (pro zjednodušení předpokládáme, že přítok vody během okamžiku t je konstantní). Za stejný okamžik se z jezera odpaří čás vody. Množství odpařené vody závisí na rychlosti odpařování k₁[ms^-1] a ploše hladiny S [m²]. Celkově se za okamžik t odpaří množství vody rovné tk₁S. Zbytek vody, který se neodpaří, se v jezeře uloží a způsobí zvýšení hladiny o výšku y (přitom předpokládáme, že plocha hladiny je pro celý přírůstek výšky y konstantní), takže se v jezeře uloží množství vody rovné yS. Celá rovnice zákona o zachování hmoty je pak :

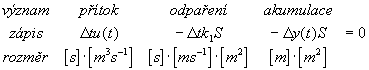
Všimněme si v rovnici (4.1) provedené rozměrové kontroly. Rozměry všech sčítanců v rovnici musí být stejné. Rozměrová kontrola je nejjednodušší způsob, jak si ověřit správnost postupu při sestavování rovnice. Nemusí však ukázat všechny naše chyby. Rovnici (4.1) upravíme dělením t a provedeme limitní přechod --> d. Dostaneme diferenciální rovnici :

která popisuje chování výšky hladiny jezera v závislosti na přítoku vody. V rovnici vystupují parametry k₁ a S, které však nejsou konstantní. Zatímco rychlost odpařování závisí na okolí systému (teplota a vlhkost okolí), plocha hladiny závisí na výšce hladiny a profilu jezerního údolí. Rychlost odpařování můžeme zastoupit její střední hodnotou.

Závislost plochy jezera na výšce hladiny však musíme vyjádřit, např. graficky, viz obr. 4.1. Závislost plochy jezera na výšce hladiny je zde popsatelná nejspíše nějakou kvadratickou funkcí. Pro zjednodušení modelu provedeme linearizaci závislosti plochy hladiny na výšce hladiny. Skutečnou závislost popíšeme pomocí lineární závislosti, jak je ukázáno na obr. 4.1. Přitom musíme zajistit, aby linearizovaný průběh procházel počátkem souřadnicového systému, např. posunutím počátku souřadnicového systému. Linearizace je velmi častý způsob zjednodušování modelů. Závislost plochy hladiny na výšce hladiny je pak:

Z rovnic (4.2) a (4.3) pak můžeme vyjádřit závislost derivace výšky hladiny na čase (to je vlastně rychlost změn výšky hladiny) :

Tím jsme získali matematický popis chování výšky jezera a současně také jeho matematický model. Všimněme si však důležité skutečnosti. Při úpravě rovnice jsme provedli dělení plochou S. To je možné jen tehdy, pokud nemůže být plocha hladiny S nulová, nebo-li při práci s modelem takový případ musíme vyloučit.

Simulační model ledovcového jezera

Ukažme si nyní sestavení simulačního modelu systému výšky hladiny jezera, který byl popsán rovnicí (4.4). Nejprve sestavíme bloky, které vytvoří hodnotu pravé strany rovnice. Tak získáme hodnotu derivace výšky hladiny. Tuto hodnotu budeme integrovat, čímž získáme hodnotu výšky hladiny. Celý simulační model je na obr. 4.2 {soubor JEZERO.SIP}. Jako vstupní veličina je přiveden jednotkový skok polohy (Heavisedeův skok), řešením modelu pro čas t = <0; 200> [den] získáme přechodovou charakteristiku systému, viz obr. 4.3.

Verifikace simulačního modelu ledovcového jezera

Jakmile jsme sestavili simulační model chování jezera, ověříme si správnost modelu srovnáním s experimentálně naměřenými údaji. Vycházíme přitom ze situace, kdy přítok vody (vstupní veličina) do jezera je stálý, takže výška hladiny (výstupní veličina) se ustálila na konstantní hodnotě, protože přítok vody a odpařování je v rovnováze. Současný přítok u(0) = 0,2 m³den^-1 a současnou výšku hladiny y(0) = 2 m označíme jako nulovou, u(0) = 0, y(0) = 0. Nyní přivedeme náhle (skokem) dodatečný přívod vody o jednotku množství za jednotku času (např. o 0,8 m³den^-1). Čas ve kterém se tak stane označíme t = 0. Průběh výšky hladiny (přechodová charakteristika systému) je uvedena na obr. 4.4.

Zvyšování hladiny způsobuje také zvětšení plochy hladiny a tím také zvětšení odpařování vody. Proto po určitém čase dojde k ustálení hladiny na nové hodnotě. Systém vykazuje setrvačnost vůči změnám vstupní veličiny.
Pokud by se jezero nalézalo v údolí se svislými stěnami, pak by se hladina nezvětšovala (tedy ani odpařování) a hladina jezera by neustále stoupala, viz obr. 4.5.

Takový systém nazývámeintegrační. Je zajímavý také tím, že pro něj nelze určit statickou charakteristiku, nebo neexistuje ustálený stav pro jiné, než nulové hodnoty vstupní veličiny.

Nyní můžeme provést srovnání přechodové charakteristiky získané řešením modelu s naměřenou přechodovou charakteristikou a verifikovat (zkontrolovat) správnost modelu, případně ho upravit. Tím je model připraven pro experimentování.

Experimenty s modelem ledovcového jezera

Závěrečnou fází a také cílem celého snažení, je provedení simulace chování systému při požadovaných vstupních veličinách. Do simulačního modelu systému přivedeme vstupní veličiny požadovaných průběhů a vyřešením zjistíme odezvu výstupních veličin.
Na modelu výšky hladiny jezera řešme kolísání výšky hladiny v závislosti na přítoku vody, který je popsán rovnicí :

u(t) = 0,3 - 0,1cos(0,01t)

K experimentu využijeme model systému výšky hladiny jezera z obr. 4.2. V čase t = 0 je systém v ustáleném stavu, nebo podle rovnice (4.4) popisující model systému je derivace výšky hladiny podle času při zadaných počátečních podmínkách nulová, to znamená, že výška hladiny se nemění. Místo bloku č. 6 však připojíme bloky realizující požadovanou hodnotu vstupní veličiny, viz obr. 4.6 {soubor JEZERO1.SIP}.

Na obr. 4.7 vidíme výslednou závislost výšky hladiny na hodnotě vstupní veličiny popsané rovnicí (4.5). Vidíme, že vstupní veličina kolísá mezi hodnotami <0,2; 0,4> [m³den^-1] a způsobuje změnu hladiny v rozsahu <2, 4> [m].

V simulačním experimentu budeme dále pokračovat vyšetřováním vlivu člověka na systém. Např. se u jezera má postavit chata, která bude odebírat část vody pro své potřeby. Naším úkolem je zjistit vliv odběru vody na chování hladiny jezera. Odběr vody člověkem způsobí zmenšení přítoku vody, předpokládejme, že tato situace nastane skokem v čase t = 300 dní {soubor JEZERO2.SIP}.
Na obr. 4.8 vidíme chování hladiny pro dva různé odběry vody. Odběr 0,01 m³den^-1 způsobil téměř nepozorovatelný rozdíl oproti systému bez odběru člověkem (zobrazeno tučnou čarou). Při odběru 0,1 m³den^-1 (100 litrů vody za den) dojde k prudkému přechodu a hladina dále kolísá v hodnotách o celý metr nižších (zobrazeno tenkou čarou). Vliv na systém je tedy podstatný.

Závěr

Po sestavení matematického modelu chování výšky hladiny ledovcového jezera v závislosti na přítoku vody jsme získali možnost simulačně ověřit vliv zásahu člověka na tento systém a získat tak znalosti potřebné k rozhodnutí o povolení nebo zakázání tohoto zásahu. Jak se ukázalo, byl by požadovaný zásah příliš razantní a podstatně by ovlivnil výšku hladiny jezera. Následně pak můžeme zkoumat jaký vliv by měla změna výšky hladiny na rostliny a živočichy v jezeře apod.

4.2. Růst bakteriální populace

Druhým příkladem ( prvním je ledovcové jezero ) je řešení růstu bakteriální populace. Na tomto příkladu si podrobněji ukážeme postupné zpřesňování modelu od nejjednoduššího a nejméně přesného až k modelu velmi dobře popisujícímu chování bakteriální populace.

4.2.1. Exponenciální růst bakteriální populace

Matematický model systému exponenciálního růstu populace

Pro sestavení nejjednoduššího modelu předpokládáme, že rychlost růstu baktérií (derivace) výstupní veličiny podle času) je úměrná počtu baktérií. Předpokládáme přitom, že tato úměrnost je lineární.
Takto získáme diferenciální rovnici popisující růst bakteriální populace:

kde je k₁ - frekvence dělení baktérií [hod^-1],
y(t) - výstupní veličina - počet baktérií.
Jak uvidíme na výsledku simulace růstu populace, počet jedinců v čase poroste exponenciálně, proto se o rovnici (4.6) hovoří jako o rovnici exponenciálního růstu.

Simulační model systému exponenciálního růstu populace

Nyní sestavíme simulační model systému. Předpokládáme, že počáteční počet baktérií je y(0) = 1000 a frekvence dělení baktérií je k₁ = 0,7 hod^-1.
Nejprve definujeme použité konstanty :
YNULA = 1000,
K1 = 0,7 .

Nyní začneme sestavovat vlastní simulační model. Základem bude blok INT realizující numerickou integraci. Na jeho vstup přivedeme hodnotu derivace výstupní veličiny a na jeho výstupu dostaneme výstupní veličinu. Jako parametry přitom zadáváme především počáteční hodnotu výstupní veličiny YNULA. Výstupní hodnotu z integrátoru přivedeme do bloku ZES, který realizuje násobení konstantou, jako konstantu zadáme hodnotu K1 a výstup z bloku ZES přivedeme na vstupy integrátoru. Tím je celý model definován, viz obr. 4.9. {soubor BAKTER1.SIP}.

Nyní zavedeme simulační model do programu SIPRO. K provedení simulace zadáme potřebné časové údaje. Čas simulace začíná vždy pro t = 0 hod, zadáme tedy koncový bod t = 10 hod. Dále zadáme krok řešení numerické integrace, krok řešení = 0,01. Krok ukládání určuje které vypočtené body budou uloženy pro zobrazení grafu. Omezení velikosti paměti počítače způsobuje, že lze takto uložit nejvýše 1600 vypočtených bodů. Zvolíme tedy krok uložení = 0,1. Tím je nastavení ukončeno. Spustíme provedení výpočtu a zobrazíme časový graf řešení, viz obr. 4.10.

4.2.2. Logistický růst

Matematický model systému logistického růstu populace

Rovnice (4.6) nevystihuje skutečnost, že zároveňs buněčným dělením probíhá odumírání starých buněk a proto populace ve skutečnosti přirůstá pomaleji. Po určitém čase dojde k rovnováze mezi přírůstkem a úbytkem baktérií a počet baktérií se ustálí na konstantní hodnotě (ustálený stav). Do matematického modelu proto musíme zahrnout korekci. Předpokládáme přitom, že odumírání baktérií způsobí zmenšení frekvence dělení baktérií. Toto zmenšení bude úměrné počtu jedinců v populaci. Tak dostaneme tzv. logistickou rovnici růstu populace :

kde je k₁ - frekvence dělení baktérií bez odumírání [hod^-1],
k₂ - konstanta úměrnosti odumírání baktérií [hod^-1].

Simulační model systému logistického růstu populace

Simulační model logistického růstu populace je na obr. 4.11 {soubor BAKTER2.SIP}. Na obr. 4.12 vidíme výsledek simulace a zřetelné ustálení počtu baktérií v populaci na hodnotě y() = 1 000 000.

4.2.3. Růst podle Hutchinsonovy rovnice

Matematický model systému růstu populace podle Hutchinsonovy rovnice

Dalším zpřesněním modelu je zahrnutí skutečnosti, že aktuální ovlivnění rychlosti množení baktérií nezávisí na současném počtu baktérií, ale na počtu baktérií v minulé generaci. Zavedením této skutečnosti do matematického modelu získáme tzv. Hutchinsonovu rovnici růstu:

kde je T_d - délka buněčného cyklu [hod].

Simulační model systému růstu populace podle Hutchinsonovy rovnice

Její simulační model je na obr. 4.13{souborBAKTER3.SIP}. Na obr. 4.14 vidíme výsledek simulace a zřetelné ustálení počtu baktérií v populaci na hodnotě y() = 1 000 000.

Závěr

Postupným zvyšováním složitosti modelu jsme dospěli až do situace, kdy získaný matematický model dosahuje dobré shody se skutečností.

4.3. Růst v prostředí s omezenými zdroji

V tomto příkladu navážeme na předchozí příklad, ve kterém jsme rozebírali růst bakteriální populace. Vycházeli jsme přitom z předpokladu, že zdroje růstu nejsou nijak omezeny. Ve skutečnosti tomu tak není. Proto se nyní budeme zabývat vlivem postupného vyčerpávání zdrojů na růst populace.

Matematický model růstu v prostředí s omezenými zdroji

Při sestavování matematického modelu vyjdeme z následujících úvah. Množství dostupných zdrojů se v závislosti na velikosti populace v čase mění. Přitom platí:

kde je z - aktuální množství dostupných zdrojů,
z0 - počáteční množství dostupných zdrojů,
k₃ - spotřeba zdrojů jednoho jedince [hod^-1].

Vzhledem ke skutečnosti, že počet jedinců v populaci nemůže být záporný, musí množství dostupných zdrojů stále klesat, až klesnou pod použitelnou mez (vyčerpají se).
Vliv klesajícího množství dostupných zdrojů se zřejmě bude projevovat také přímo na růstu populace. Tento vliv bude zřejmě nepřímo úměrný množství dostupných zdrojů, připadajících na jednoho jedince:

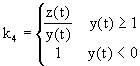
kde je k₄ - množství dostupných zdrojů připadající na bakterii.

Růst populace je pak popsán následující rovnicí:

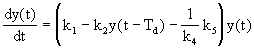
kde je k₅ - konstanta úměrnosti odumírání baktérií způsobeném nedostatkem dostupných zdrojů [hod^-1].

Simulační model růstu v prostředí s omezenými zdroji

Odpovídající simulační model je uveden na obr. 4.15 {soubor BAKTER4.SIP}.

Na obr. 4.16 vidíme průběh růstu populace, který je na svém počátku málo ovlivněn nedostupností zdrojů, proto je prakticky stejný, jako vývoj v prostředí neomezených zdrojů. Postupným poklesem množství dostupných zdrojů se populace začíná snižovat, až náhle velmi rychle zaniká.

Na obr. 4.17 je zkoumán vliv snížení frekvence dělení bakterií z hodnoty k₁ = 0,7 na k₁ = 0,6. Doba života kolonie se prodloužila za cenu zmenšení její velikosti, rychlost jejího zániku je výrazně nižší, ale zánik kolonie je samozřejmě nevyhnutelný.

Závěr

Simulací jsme zjistili jak se bude vyvíjet populace v prostředí s omezenými zdroji. Zajímavý je především prudký zánik populace, jakmile množství dostupných zdrojů výrazně poklesne.

4.4. Osídlování ostrova

Velmi zajímavý je systém osídlování ostrova jednotlivými druhy organismů. Systém je závislý pouze na předchozím počtu druhů na ostrově ( tímto se zabývala předchozí kapitola růst v prostředí s omezenými zdroji ). Systém tedy nemá vstupní veličinu, výstupní veličinou je počet druhů na ostrově.

Matematický model systému osídlování ostrova

Model systému je obvykle sestavován následovně. Za jednotku času přibude na ostrově počet druhů nepřímo úměrný vzdálenosti ostrova od pevniny a nepřímo úměrný počtu druhů na ostrově. Za stejnou jednotku času vymře na ostrově počet druhů přímo úměrný na aktuálním počtu druhů. Model je tedy obvykle sestavován v následující podobě :

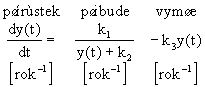
kde je
k₁ - konstanta rychlosti přírůstku druhů závislá na převrácené hodnotě vzdálenosti ostrova [rok^-1],
k₂ - konstanta rychlosti přírůstku druhů - v poměru s konstantou k₁ určuje přírůstek druhů na neosídleném ostrově,
k₃ - konstanta rychlosti vymírání druhů na ostrově [rok^-1].

Simulační model systému osídlování ostrova

Odpovídající simulační model je na obr. 4.18 {soubor OSTROV.SIP}.

Závěr

Na obr. 4.19 vidíme výsledek simulace a zřetelné ustálení počtu na hodnotě y() = 27. Použité hodnoty konstant odpovídají osídlování ostrova Krakatoa ptactvem po katastrofě v roce 1883 do roku 1921.

4.5. Systém příjmu potravy

Systém příjmu potravy ( který nepřímo souvisí s kapitolou osidlování ostrova ) je popsán pomocí čtyř stavových veličin, které definují jeho okamžitý stav (někdy jsou označovány jako kompartmenty). Na obr. 4.20 je zobrazena interakce jednotlivých prvků systému (popsaných stavovými veličinami) za jednotku času. Význam stavových veličin je následující :
C₁ - koncentrace určité složky potravy v žaludku,
C₂ - koncentrace určité složky potravy v krvi,
C₃ - koncentrace určité složky potravy ve tkáních,
C₄ - koncentrace určité složky potravy v moči.

Matematický model systému příjmu potravy

Za jednotku času dojde k předání určité složky potravy mezi jednotlivými prvky systému a tím ke změně hodnot stavových veličin, které je popisují. Jednotlivé výměny za jednotku času popisují konstanty uvedené na obr. 4.20. Na jeho základě můžeme zapsat matematický model systému :

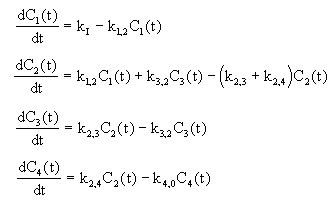
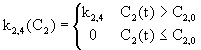
Simulační model systému příjmu potravy

Na obr. 4.22 {soubor POTRAVA.SIP} je uveden simulační model systému příjmu potravy pro případ, kdy v čase t = 0 byl žaludek naplněn potravou C₁(0) = 10 [jednotka potravy] a další přísun potravy se neuskutečňuje (k_I= 0). Skutečnost, že přesun složky potravy z krve do moče probíhá až po překročení určité hladiny koncentrace je realizována pomocí bloků č. 13 a 14. Na obr. 4.23 vidíme výsledek chování systému.
Hotový model využijeme k simulaci chování systému příjmu potravy při dávkovém přísunu potravy. Potrava bude přiváděna do systému v malých množstvích v pravidelných intervalech. Model systému doplníme o bloky realizující tuto skutečnost, viz obr. 4.21 {soubor POTRAVA2.SIP}. Současně změníme počáteční podmínku C₁(0) = 0.

Na obr. 4.24 je zobrazen průběh vstupní veličiny do systému (přísun potravy), na obr. 4.25 pak chování systému.

Závěr

Na simulačním modelu jsme ukázali chování systému příjmu potravy. Jednoduchou změnou vstupního přísunu potravy můžeme zkoumat jeho vliv na chování systému, zátěž jednotlivých prvků systému apod.

4.6. Systém kořist-dravec

Často používaným je model systému kořist - dravec ( což je zjednodušená aplikace kapitoly systém příjmu potravy ), viz obr. 4.26. Předpokládáme, že kořist má neomezený přísun potravy a dravci se živí jen touto kořistí. Jedná se o dosti podstatné zjednodušení, ale jak si ukážeme i tak můžeme učinit řadu zajímavých zjištění.

Matematický model systému kořist-dravec

Systém můžeme popsat dvojicí rovnic. První rovnice popisuje změnu množství kořisti. Předpokládáme přitom, že změna množství kořisti je způsobena přírůstkem kořisti díky rozmnožování a hubením kořisti dravci, přirozená úmrtnost kořisti se neuvažuje:

kde je
x(t) - množství kořisti,
y(t) - množství dravců,
k₁ - konstanta určující relativní rodivost kořisti za jednotku času,
k₂ - konstanta určující relativní kořistění (je závislé jak na množství dravců, tak množství kořisti).

Druhá rovnice popisuje změnu množství dravců za jednotku času :

kde je k₃ - parametr účinnosti přeměny energie z biomasy kořisti na biomasu dravců,
k₄ - relativní úmrtnost dravců.

Simulační model systému kořist-dravec

Na obr. 4.27 {soubor KOR_DRAV.SIP} je uveden simulační model systému kořist-dravec. Na obr. 4.28 vidíme výsledek chování systému pro dva případy. Tučnou čarou je zobrazeno chování systému bez zásahu člověka. Předpokládaná rodivost kořisti je k₁ = 0,4. Tenkou čarou je zobrazen systém se zásahem člověka, který odloví část kořisti, toto odlovení je úměrné aktuálnímu množství kořisti a proto ho můžeme do modelu zavést jako snížení rodivosti kořisti na hodnotu k₁ = 0,2. Vidíme, že průměrná hodnota, kolem které kmitalo množství kořisti zůstala zachována, pouze se zmenšila amplituda kmitání. U dravců však dojde ke snížení průměrného množství dravců. Znamená to, že zásah ve skutečnosti ovlivnil hlavně dravce.

Na stejném modelu nyní ukažme vliv člověka, který způsobí svými zásahy zvýšení relativní úmrtnosti dravců o 50%, z hodnoty k₄ = 1,2 na hodnotu k₄ = 1,8. Na obr. 4.30 je tučně zobrazeno chování systému bez zásahu člověka, tence se zásahem. Vidíme, že průměrná hodnota, kolem které kmitalo množství kořisti se výrazně zvýšila, amplituda kmitání se zvýšila rovněž. Množství dravců sice sleduje vývoj množství kořisti, ale v minimech je množství dravců tak malé, že hrozí jejich úplné vyhubení.

Verifikace simulačního modelu systému kořist-dravec

Provedené simulační výstupy je nutno nyní verifikovat s výsledky pozorování systému v přírodě, může to být např. systém hraboši-káňata, viz obr. 4.32. Přitom si musíme uvědomit, že již tato pozorování jsou z technického pohledu zatížena dosti značnou chybou a to řádově i přes 5 - 10%. Dosažení shody simulačního výstupu s pozorováním s přesností na 5 - 10% je tedy možno považovat za dostatečné.

Experimenty s modelem systému kořist-dravec

Simulační model je nyní připraven k experimentům. Ukažme si nyní např. zjištění, jak bude systém reagovat na plynulé zhoršování životního prostředí, které způsobí, že během následujících 100 let dojde ke snížení relativní rodivosti kořisti na polovinu současné hodnoty a současně zvýšení relativní úmrtnosti dravců o polovinu současné hodnoty. Výsledek simulace vidíme na obr. 4.33 {soubor KOR_DRA2.SIP}.

Závěr

Sestavili jsme zjednodušený matematický model systému kořist-dravec a provedli simulaci jeho chování. Srovnáním s naměřenými hodnotami byla zjištěna dobrá shoda se skutečností. Pomocí simulačních experimentů jsme pak mohli předpovědět jaký bude další vývoj tohoto systému v závislosti na působení člověka.

4.7. Přenos energie v jezerním ekosystému

Posledním modelem ( předchozí modely byly systém příjmu potravy a systém kořist-dravec ) je zjednodušený systém přenosu energie v jezerním ekosystému. Celý systém je poměrně komplikovaný, jak vidíme na obr. 4.34.

Pro naše potřeby provedeme zjednodušení, budeme předpokládat, že systém obsahuje tři prvky - rostliny, herbivory a karnivory. Vstupem do systému je energie slunečního záření. Stav jednotlivých prvků popisují stavové veličiny, které vyjadřují množství biomasy udané jako energie vázaná v biomase vztažená na jednotku plochy nebo objemu. Na obr. 4.35 vidíme schéma předávání biomasy za jednotku času.

Část biomasy se přitom ztrácí respirací a část jiným propadem energie (odumírání, exkrementy). Konstanty uvedené v obr. 4.35 udávají rychlost přenosu energie z jednoho prvku systému do druhého, jejich rozměrem je [rok^-1]. Za jednotku času se tedy přenese množství energie dané součinem konstanty a aktuálního množství biomasy ve zdrojovém prvku.

Matematický model přenosu energie v jezerním ekosystému

Celý systém pak můžeme popsat pomocí trojice stavových rovnic (člen 1/365 slouží ke změně rozměru konstant z [rok^-1] na [den^-1]) :

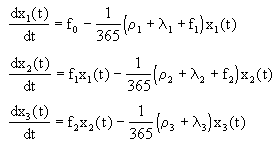
kde je
f₀ - energetický vstup sluneční energie [kJ m_-2den^-1],
x₁ - energie biomasy rostlin [kJ m^-2],
x₂ - energie biomasy herbivorů [kJ m^-2],
x₃ - energie biomasy karnivorů [kJ m^-2],
_i - rychlost ztráty biomasy respirací [rok^-1],
_i - rychlost ostatních ztrát biomasy [rok^-1],
f_i - rychlost toku biomasy mezi prvky systému.
Energetický vstup sluneční energie do systému je přitom popsán rovnicí :

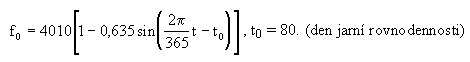
Průběh vstupu sluneční energie je zobrazen na obr. 4.36.

Hodnoty potřebných konstant uvádí následující tabulka :

i	prvek systému	počáteční hodnota	rychlost toku energie	rychlost ztrát respirací	rychlost jiných ztrát
			fi	i	i
		[kJ.m-2]	[rok-1]	[rok-1]	[rok-1]
1	rostliny	250 000	0,48	1	2,55
2	herbivoři	7 000	4,85	6,9	6,12
3	karnivoři	8 000		2,7	1,95

Simulační model přenosu energie v jezerním ekosystému

Na obr. 4.37 {soubor JEZ_EKOS.SIP} je uveden simulační model systému přenosu energie v jezerním ekosystému. Na obr. 4.38 vidíme výsledek chování systému. Pro lepší zobrazení bylo pro průběh x₂ a x₃ použito jiné měřítko - na pravé straně grafu.

---

---

4.8. Literatura k ekologickým systémům

DYKYJOVÁ, D. aj. 1989. Metody studia ekosystémů. Praha: Academia, 1989.
FARB, P. 1977. Ekologie. Praha: Mladá fronta, 1977.
KŘÍŽOVÁ, E. aj. 1992. Všeobecná ekológia. Zvojen: TU, 1992.
KVASNIČKOVÁ, D. 1991. Základy ekologie. Praha: SPN, 1991.
LOSOS, B. aj. 1984. Ekologie živočichů. Praha: SPN, 1984.
LOSOS, B. aj. 1987. Základy obecné ekologie. Praha: SPN, 1987.
MADER, S. S. 1988. Inquiry into Life. Iowa: Dubuque, Wm.C.Brown Publishers, 1988.
Metodika biomonitoringu v CHKO a NP. Praha: MŽP ČR, 1992.
NEUMANNOVÁ, M. a FARANA, R. 1994. Ekologie. Prozatímní učební text. Ostrava: Katedra ochrany životního prostředí HGF VŠB, 1994.
NAVÁK, M., FÁBER, J. a KUFUDAKI, O. 1993. Neuronové sítě a informační systémy živých organismů. Praha: Grada, 1993
ODUM, E. P. 1977. Základy ekologie. Praha: Academia, 1977.
PAZOUREK, J. 1992. Simulace biologických systémů. Praha, Grada, 1992.
PIVNIČKA, K. 1988. Ekologie. Praha: SPN, 1988.
SLAVÍKOVÁ, J. 1986. Ekologie rostlin. Praha: SPN, 1986.
STARR, C. 1991. Biology - Concept and Aplicantion.Wadsworts: Publishing Company, 1991.
STILING, P. D. 1992. Introductory Ecology. Prentice Hall, Inc., A Simon & Schuster Company, Englewood Cliffs, New Jersey, 1992.
TöLGYESSY, J. a FARGÁŠOVÁ, A. 1986. Základy ekológie a toxikológie. Bratislava: STU, 1986.