1. Základní pohyby těles

První kapitolou je řešení základních pohybů těles. V souladu s ustálenou praxí se budeme zabývat tělesy, která si představíme v podobě hmotného bodu, pohybujícího se v prostředí bez odporu (vakuum). Jako první uvedeme přímočarý zrychlený pohyb, u kterého nebudeme uvažovat působení přitažlivosti, pak vrh svislý s působením přitažlivosti a jejich složením dostaneme vrh šikmý. Pro simulaci pohybů použijeme simulační program SIPRO [VÍTEČEK, A. a FARANA, R., aj. 1996.]. Jeho obsluhu si nastíníme u prvního příkladu, podrobně se jí zabývat nebudeme, nebo program je vybaven podrobnou příručkou pro uživatele.

1.1. Přímočarý zrychlený pohyb

Přímočaré pohyby jsou v kinematice popsány základními veličinami, jsou to s -dráha [m], v - rychlost [m s^-1], a - zrychlení [m s^-2]. Jejich vzájemný vztah určíme následujícím postupem. Vezměme krátký časový úsek označený t [s]. Budeme předpokládat, že v tomto čase se těleso pohybuje stálou rychlostí v a urazí dráhu s [m], odtud tedy platí:

Obdobně budeme předpokládat, že pokud bude v tomto krátkém časovém úseku na těleso působit konstantní zrychlení a dojde ke zvýšení rychlosti o v, tedy platí:

Jestliže budeme v rovnici (1.2) zmenšovat časový úsek , tedy provedeme limitní přechod - d, obdržíme diferenciální rovnici pro určení dráhy, kterou těleso urazí při působení zrychlení a:

Diferenciální rovnici (1.3) můžeme řešit velmi jednoduše, např. postupnou integrací, takže získáme následující vztah pro určení dráhy s v čase t. Přitom předpokládáme, že čas se začíná počítat od okamžiku počátku pohybu.

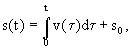
resp.

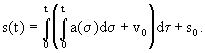
kde je	t	- čas,
	s(t)	- dráha, kterou těleso urazilo od počátku pohybu do okamžiku t,
	s0	- počáteční dráha tělesa, nejčastěji bude s0= 0,
	v(t)	- rychlost tělesa v čase t,
	v0	- počáteční rychlost tělesa, nejčastěji bude v0= 0,
	a(t)	- zrychlení tělesa v čase t.

Rovnice (1.4) jsou matematickým modelem přímočarého pohybu. Přitom jak rychlost, tak zrychlení se mohou v průběhu pohybu měnit - mohou být funkcí času, což bude komplikovat jeho řešení.
Řešením některé z rovnic (1.4) pro konkrétní hodnoty získáme průběh dráhy tělesa v závislosti na čase. Můžeme tak učinit analyticky. Pokud by však průběh zrychlení byl popsán nějakým složitějším vztahem, může se stát, že analytické řešení nebudeme schopni určit. Řešení tedy provedeme numericky (přibližně).
Matematický model převedeme do tvaru vhodného pro řešení zvoleným programem. V našem případě to bude simulační program SIPRO pracující se simulačním modelem, který je vlastně zápisem matematického modelu pomocí jednoduchých funkčních bloků. Program SIPRO jich zná celkem 71 druhů.
Převod začneme tím, že si pojmenujeme konstanty, se kterými budeme v simulačním modelu pracovat. Např.:

A0 - počáteční zrychlení,
V0 - počáteční rychlost,
S0 - počáteční dráha.

Nyní již sestavíme vlastní model. Základem bude blok řešící numerickou integraci, v programu SIPRO nese název INT. Tento blok současně provádí vážený součet dvou vstupních hodnot, což pro nás není potřeba. Na oba vstupy přivedeme rychlost v(t). K výstupu bloku potřebujeme ještě přičíst hodnotu počáteční dráhy s₀ (pomocí bloku SUM), tak získáme hodnotu dráhy s(t). Hodnotu rychlosti v(t) však neznáme, určíme ji obdobně integrací zrychlení a₀ a přičtením počáteční rychlosti v₀. Přímočarý rovnoměrně zrychlený pohyb je charakteristický tím, že zrychlení je po celou dobu pohybu konstantní, hodnotu a₀ tedy přivedeme na oba vstupy integrátoru, na jeden s vahou 1, na druhý s vahou 0. Tím jsme získali celý simulační model, viz obr. 1.1 {soubor PRIM_POH.SIP}.

Tento model nyní zapíšeme do prostředí programu SIPRO, na obr. 1.2 je zobrazena situace, kdy kurzor stojí na prvním řádku. Postup práce je velmi jednoduchý, program navíc obsahuje podrobnou kontextovou nápovědu, takže se jím nebudeme zabývat.

Nyní budeme chtít zjišovat průběh pohybu tělesa pro různé případy. Nejjednodušším případem je přímočarý rovnoměrně zrychlený pohyb, kdy na nepohybující se těleso (s₀ = 0 m, v₀ = 0 ms^-1) začíná v čase t = 0 s působit konstantní zrychlení a = 0,2 ms^-2. Řešení provedeme v čase t = <0; 10> [s] s krokem řešení 0,1 s. Na obr. 1.3 vidíme průběh rychlosti (čárkovaně), která lineárně narůstá a průběh dráhy (plnou čarou), která narůstá kvadraticky.

Zajímavý může být také průběh rychlosti v závislosti na dráze, jak vidíme na obr. 1.4.

Závěr

V tomto příkladě jsme provedli sestavení matematického modelu přímočarého rovnoměrně zrychleného pohybu, sestavení odpovídajícího simulačního modelu a jeho řešením ověření správnosti modelu. Zjistili jsme, že u přímočarého zrychleného pohybu s konstantním zrychlením rychlost lineárně narůstá a dráha narůstá kvadraticky.

1.2. Rovnoměrně zrychlený pohyb bodu po kružnici

Tento pohyb vychází ze základních veličin kapitoly přímočarý zrychlený pohyb.
Pohyb bodu po kružnici je v kinematice popsán základními veličinami: j - úhlová dráha [rad], w - úhlová rychlost [rad s^-1], e - úhlové zrychlení [rad s^-2]. V krátkém časovém úseku t [s] budeme předpokládat, že bod se pohybuje stálou rychlostí w a urazí dráhu j, pak platí:

Pokud bude v tomto krátkém časovém úseku na bod působit konstantní úhlové zrychlení e dojde ke zvýšení rychlosti o w, pak platí:

Jestliže budeme v rovnici (1.6) zmenšovat časový úsek , tedy provedeme limitní přechod - d, obdržíme diferenciální rovnici pro určení úhlové dráhy j, kterou bod urazí při působení úhlového zrychlení e:

Diferenciální rovnici (1.7) můžeme řešit velmi jednoduše, např. postupnou integrací, takže získáme následující vztah pro určení úhlové dráhy j v čase t.

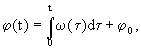
resp.

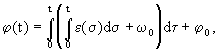
kde je t - čas,

j(t) - úhlová dráha, kterou bod urazil od počátku pohybu do okamžiku t,
j0 - počáteční úhlová dráha bodu,
w(t) - úhlová rychlost bodu v čase t,
w0 - počáteční úhlová rychlost bodu,
e(t) - úhlové zrychlení bodu v čase t.

Tento pohyb lze vyšetřovat v různých souřadnicích:
a) V kartézských souřadnicích (obr. 1.5) je pohyb bodu L popsán rovnicemi:

x(t) = r cos j(t),

Pak rychlost ve směrech x a y je dána vztahy:

a zrychlení je:

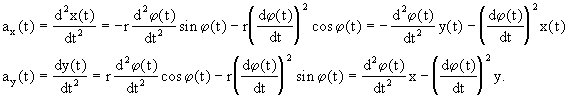
b) V soustavě tečna, normála je pohyb bodu L po kružnici popsán rovnicemi:

odlehlost s(t) = rj(t),

Rovnice (1.8) jsou matematickým modelem pohybu bodu L po kružnici. Zároveň si vyjádříme pomocí simulačního modelu dráhu, rychlost a zrychlení v pravoúhlých souřadnicích a odlehlost, rychlost, tečné a normálové zrychlení v souřadnicové soustavě tečna, normála.

Převod začneme tím, že si pojmenujeme konstanty, se kterými budeme v simulačním modelu pracovat. Např.:

e₀ - počáteční úhlové zrychlení,
w₀ - počáteční úhlová rychlost,
j₀ - počáteční úhlová dráha,
r₀ - poloměr kružnice.

Nyní sestavíme blokové schéma simulačního programu SIPRO.

Model zapíšeme do editoru v prostředí simulačního programu SIPRO {soubor KR_POH1.SIP}.
Nyní budeme zjišovat průběh pohybu bodu pro různé případy. Nejjednodušším případem je rovnoměrně zrychlený pohyb bodu po kružnici o poloměru r₀ = 0,1 m, kdy na hmotný bod začíná v čase t = 0[s] působit konstantní úhlové zrychlení e₀ = 0,4 rad s-2. Bod je na kružnici umístěn v poloze j₀ = 0,5 rad. Řešení provedeme v čase t = <0; 12> [s] s krokem řešení 0,1 s. Na obr.1.8 vidíme průběh rychlosti (čárkovaně), která lineárně narůstá a průběh dráhy (plnou čarou), která narůstá kvadraticky.

Při vyšetřování pohybu v soustavě tečna, normála můžeme sledovat tečné a normálové zrychlení, dráha, atd. Zajímavý je průběh velikosti zrychlení v závislosti na čase, jak je vidět na obr.1.9. Vyšetřování pohybu bodu po kružnici v kartézských souřadnicích vede ke sledování pohybu bodu po kružnici ve skutečnosti. Na obr.1.10 si můžete všimnout, že se jedná o pohyb zrychlený. Projevuje se to v postupném prodlužování vykreslovaných úseků na šroubovici.

Rovněž je možno sledovat pohyb bodu po kružnici, jejíž poloměr nebude konstantní. Např. poloměr rovnoměrně narůstá (obr. 1.11), poloměr se mění goniometricky (obr. 1.12). Tyto pohyby pak můžete najít v souborech KR_POH2.SIP a KR_POH3.SIP.

1.3. Vrh svislý

Vrh svislý je vlastně přímočarý rovnoměrně zrychlený pohyb, při kterém těleso o hmotnosti m [kg] vypustíme s určitou počáteční rychlostí v₀ [m s^-1] vzhůru a to se pohybuje za současného působení zemské gravitace. Gravitace na těleso působí jako zrychlení g9,81 m s^-2. Působí však proti směru pohybu. Celou situaci můžeme znázornit následovně, viz obr. 1.13.

Matematický model tohoto systému bude tedy shodný s předchozím příkladem přímočarého pohybu, pouze zrychlení má opačný smysl, což zavedeme do modelu zadáním opačného znaménka (váhy -1) v bloku INT (č. 14). Výsledný model je na obr. 1.14, {soubor VRH_SVIS.SIP}.

Simulaci provedeme pro počáteční rychlost v₀ = 20 m s^-1 = 72 km h_-1. Pro lepší představu, této rychlosti dosahuje běžně nárazový vítr. Na obr. 1.15 vidíme průběh dráhy (plnou čarou), která nejprve narůstá a pak začíná klesat. Způsobuje to vliv gravitačního zrychlení. Na obr. 1.15 je šipkou zvýrazněn kulminační bod dráhy. Po jeho dosažení těleso začíná klesat. Rychlost pohybu (čárkovaná čára) lineárně klesá.

Na obr. 1.16 je pro zajímavost zobrazen průběh rychlosti v závislosti na dráze.

Zvláštním případem vrhu svislého je volný pád. Nastává tehdy, když je počáteční rychlost nulová. Tento případ ponecháváme na samostatné experimentování.

1.4. Vrh šikmý

Dalším důležitým pohybem je vrh šikmý, při kterém je těleso o hmotnosti m [kg] uvedeno do pohybu ve směru, který svírá s vodorovným směrem úhel [^o]. Tento pohyb si můžeme představit jako současné působení dvou samostatných pohybů, jestliže působení počáteční rychlosti v₀ [m s^-1] rozložíme do vodorovného a svislého směru, jak vidíme na obr. 1.17.

Těleso tedy vykonává rovnoměrný přímočarý pohyb s počáteční rychlostí v_x = v₀ cos a [m s^-1] a nulovým zrychlením. Současně vykonává vrh svislý s počáteční rychlostí v_y = v₀ sin [m s^-1].

Simulační model vrhu šikmého tedy nejsnáze vytvoříme složením modelu pro pohyb přímočarý z obr. 1.1 a modelu pro vrh svislý z obr. 1.14. Výsledný model doplním o určení příslušných počátečních rychlostí, výsledek je na obr. 1.18 {soubor VRH_SIK.SIP}. Úhel budeme zadávat ve stupních, program však pracuje s úhly vyjádřenými v radiánech. Přepočet ze stupňů na radiány je realizován násobením konstantou p/180 0,01745329.

Simulaci provedeme pro hodnotu v₀ = 20 m s^-1. Nejprve pro hodnotu úhlu = 90^o, výsledek zobrazíme tučnou čarou. A pak pro = 45^o, výsledek zobrazíme tenkou čarou. Na obr. 1.19 vidíme průběh dráhy (plnou čarou) a rychlosti (čárkovanou čarou) přímočarého pohybu ve vodorovném směru. Pro nastavení = 90^o se vlastně jedná o vrh svislý, rychlost i dráha jsou tedy nulové.

Na obr. 1.20 vidíme průběh dráhy (plnou čarou) a rychlosti (čárkovanou čarou) pro pohyb ve svislém směru. Pro nastavení = 90^o (tučnou čarou) jsou výsledky shodné s předchozím příkladem 1.3. Tím jsme současně ověřili správnost modelu.
Na obr. 1.21 nyní zobrazíme průběh dráhy ve směru svislém s_y v závislosti na dráze ve směru vodorovném s_x. Tak získáme průběh skutečné dráhy tělesa.

Nyní můžeme experimentovat s modelem, měnit počáteční rychlost, úhel apod. Zvláštní případ vrhu šikmého získáme pro = 0^o. Nazývá se vrh vodorovný.

1.5. Kyvadlo

Budeme sledovat pohyb hmotného bodu o hmotnosti m [kg], který se pohybuje po svislé kružnici realizované otočně uloženou tyčí neproměnné délky l [m] a zanedbatelné hmotnosti za působení tíhové síly F_G [N]. Tento děj se nazývá matematické kyvadlo (obr. 1.22). Sestavíme pohybovou rovnici a rozepíšeme ji do os vhodného souřadnicového systému.

Po zavedení reakčního účinku tyče F_R[N] bude její pohybová rovnice:

Rovnice (1.22) je zároveň matematickým modelem kyvadla, z něhož vytvoříme blokové schéma pro simulační program SIPRO (obr. 1.23) {soubor KYVADLO.SIP}. Počáteční hodnotou pro tento děj je nastavený úhel j₀ v čase t = 0 s. Děj probíhá do ustálení kyvadla v poloze, kdy je úhel j = 0.

Simulaci provedeme pro počáteční úhel j_o = 30^o (obr. 1.24), j_o = 90^o (obr. 1.25) a j_o = 180^o (obr. 1.26, obr. 1.27). Úhel j_o lze zadávat ve stupních, i když program pracuje s úhly vyjádřenými v radiánech. Přepočet je realizován násobením konstantou p/180. V grafech je však úhlová dráha vyjádřena v radiánech z hlediska možnosti přehledného zobrazení úhlové dráhy a úhlové rychlosti v jednom grafu.

Pohyb kyvadla závisí na přesnosti zadané hodnoty p, což je nejvíce viditelné v případě, kdy j_o = 180^o. Experimentováním s nastavením hodnoty p různé přesnosti pak získáme různé průběhy pohybu kyvadla v závislosti na čase (obr. 1.26, obr. 1.27).

Zajímavý je také průběh úhlové rychlosti v závislosti na úhlové dráze a čase (rozšířený stavový graf) pro různé hodnoty j_o, zobrazený na obr. 1.28 a obr. 1.29.

Dále můžeme experimentovat s modelem, měnit jeho počáteční úhel j_o a hodnotu p nebo zavést tlumení, vliv počáteční síly ve směru pohybu či v protisměru pohybu atd. Zajímavá je rovněž úvaha o nastavení počátečního hodnoty úhlu v intervalu (0^o, 180^o) a (180^o, 360^o) a jeho vlivu na ustálenou hodnotu. Ustálená hodnota pak bude vždy 2kp, kde k nabývá hodnot 0, 1, 2,...

1.6. Pohyb vázaného bodu - pohyb po nakloněné rovině

Pohyb po nakloněné rovině je přímočarý zrychlený pohyb, při kterém těleso o hmotnosti m [kg] položené na nakloněnou rovinu se pohybuje směrem dolů s rovnoměrným zrychlením, které způsobí zemská gravitace (obr. 1.30).

Pohybová rovnice pro tento pohyb je:

Pohybovou rovnici rozepíšeme do jednotlivých složek pravoúhlého souřadnicového systému, kde osa t (tečná) je shodná se sklonem roviny a osa n (normálová) je na rovinu kolmá. Tedy platí:

Pro třecí a normálovou sílu platí vztah:

Z rovnice (1.24) pak vyplývá:

Gravitační síla je přímo úměrná hmotnosti bodu:

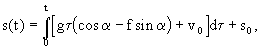
Rovnice (1.29) je matematickým modelem pohybu po nakloněné rovině. Matematický model převedeme do tvaru vhodného pro řešení simulačním programem SIPRO (obr. 1.31) {soubor NAKL_RO1.SIP}.

Simulaci provedeme pro počáteční rychlost v_o = 0 m s^-1, počáteční dráhu s_o = 0 m, úhel sklonu roviny a = 30^o (což je 0,524 rad - v programu SIPRO zadáváme úhel v radiánech, ale můžeme jej upravit i pro zadávání ve stupních, viz předchozí příklad) a koeficient tření f = 0,15. Na obr. 1.32 vidíme průběh dráhy (plnou čarou) v závislosti na čase, který narůstá kvadraticky. Rychlost (čárkovanou čarou) tělesa v závislosti na čase narůstá lineárně. Předpokládáme, že hodnoty pro zadávání úhlu sklonu roviny jsou z intervalu <0, p/2>.

1.7. Pohyb vázaného bodu - pohyb po nakloněné rovině s přechodem na vodorovnou plochu

Variantou pohybu po nakloněné rovině může být např. pohyb po nakloněné rovině, který přechází do pohybu po vodorovné ploše (obr. 1.33). Pohyb tělesa na vodorovné ploše se zastaví, protože budeme předpokládat tření při pohybu tělesa po rovině. Celkově tedy můžeme rozdělit pohyb do dvou částí: pohyb po nakloněné rovině a pohyb po rovině. Můžeme určit, že těleso o hmotnosti m [kg] na nakloněné rovině urazí dráhu h₁ [m] a na rovině se zastaví ve vzdálenosti h₂ [m] od přechodu těchto rovin.

Budeme vycházet z matematického modelu předchozího příkladu 1.6 (obr. 1.34) a sestavíme vlastní simulační model, soubor {NAKL_RO2.SIP}.
Při simulaci tohoto pohybu použijeme další specifické bloky pro vyřešení obou částí pohybu. Bloky XVY a XEY (bloky č. 2 a 4) logicky rozhodují o tom, o který pohyb se právě jedná. Předem víme, že těleso v první části urazí vdálenost h₁. V této části je nastaven v našem případě úhel sklonu roviny a = 0,524 rad. V okamžiku, kdy vzdálenost je větší než h₁, výpočet probíhá s úhlem sklonu a₁ = 0 rad. Veličina s_K(t) a v_K(t) jsou výslednými hodnotami pohybu. Program SIPRO logicky nerozpozná, že rychlost v(t) je nulová a tím, že se těleso zastavilo. To je vyřešeno opět blokem XVY (č. 21), který testuje rychlost na hodnotu 0. Protože ihned na začátku je rovněž rychlost nulová, musíme nastavit počáteční rychlost na hodnotu větší než 0, v našem případě v₀(t) = 0,00000001 m s^-1. Tato rychlost je zanedbatelná vzhledem k velikosti kroku výpočtu, který byl v našem případě nastaven na hodnotu 0,02.
Je zřejmé, že dráha při zastavení tělesa zůstává konstatní. Přesto, že byl použit blok IN0 (č. 17) místo obvyklého bloku INT, který provede vynulování, na výstupu bloku SUM (č. 20) není hodnota konstatní, ale mírně klesá.
Blok MEM (č. 23) si pamatuje maximální hodnotu na výstupu bloku SUM (č.20), čímž dosáhneme konstantní hodnoty při zastavení tělesa. Tato konstatní dráha je vlastně součtem vzdálenosti h₁ a h₂ (obr. 1.33).

Simulaci jsme provedli pro tyto počáteční hodnoty: s_o = 0 m, v_o = 0,00000001 m s^-1, h₁ = 0,5 m, a = 0,524 rad, a₁ = 0 rad, f = 0,15 a g = 9,81 m s^-2. Na obr. 1.35 je zobrazen průběh dráhy a rychlosti tělesa v závislosti na čase. Je opět možné vidět, že rychlost tělesa roste či klesá lineárně a dráha kvadraticky v závislosti na čase.

Také můžeme identifikovat, že těleso na nakloněné rovině urazí kratší vzdálenost, než za jakou se zastaví na rovné ploše. Z toho vyplývá, že těleso má větší zrychlení na nakloněné rovině než na rovné ploše, kdy má také zrychlení opačný smysl (těleso brzdí). Důkazem toho je obr. 1.36, kde je tečkovanou čarou zobrazeno zrychlení tělesa.

Závěr

Sestavili jsme matematický model pohybu tělesa po nakloněné rovině s přechodem pohybu po vodorovné ploše. Ukázali jsme si využití logických a paměových bloků pro jednoduchý složený pohyb Kombinace jakýchkoliv jiných základních pohybů můžete sami zkusit vytvořit na základě těchto ukázkových příkladů.

1.8. Pohyb tělesa v pružném prostředí

Máme za úkol vyřešit pohyb tělesa o zadané hmotnosti m [kg], které je vázáno (upevněno) k tuhému rámu a v čase t = 0 s na něj začíná působit síla F [N]. Těleso opět zastoupíme hmotným bodem o hmotnosti m [kg], upevnění nahradíme působením pružiny s danou konstantou tuhosti k [N m^-1] a tlumením s udaným koeficientem tlumení B [N s m^-1]. Na obr. 1.37 je symbolicky zakreslena celá situace.

Na těleso působí čtyři síly, které musí být v rovnováze:

Z rovnice (1.30) vyjádříme druhou derivaci polohy tělesa:

Řešení provedeme pro konkrétní nastavení parametrů m = 1 kg, k = 1 N m^-1, B = 0,5 N s m^-1, F = 10 N. Na obr. 1.39 je znázorněn průběh polohy (plná čára) a rychlosti (čárkovaná čára) pohybu tělesa. Vidíme na něm, že těleso je z počáteční klidové polohy uvedeno do kmitavého tlumeného pohybu. Po jeho odeznění se poloha ustaluje na nové hodnotě.

Velmi zajímavý je také průběh rychlosti v závislosti na poloze tělesa, viz obr. 1.40. Znázorňuje velmi dobře, jak se rychlost po prudkém nárůstu postupně snižuje a poloha tělesa se ustaluje na nové poloze.

Do grafu závislosti rychlosti na poloze tělesa můžeme přidat zobrazení času, jak vidíme na obr. 1.41. Na dopředné ose (x) je čas, na vodorovné ose (y) je poloha a na svislé ose (z) je rychlost.

1.9. Pohyb dvojice vázaných těles

Dalším příkladem je řešení pohybu dvou těles, z nichž jedno těleso o hmotnosti m₁ [kg] je upevněno k tuhému rámu a k němu je upevněno těleso druhé o hmotnosti m₂ [kg] (řešení pohybu pouze jednoho tělesa je v kapitole pohyb tělesa v pružném prostředí). Vazbu tělesa k rámu opět nahradíme působením tlumení B₁ [N s m^-1] a pružiny k₁ [N m^-1], vazbu mezi tělesy působením pružiny k₂ [N m^-1], jak vidíme na obr. 1.42. Zátěžná síla F [N] přitom působí na druhé těleso.

Pro řešení této soustavy těles provedeme nejprve uvolnění těles a zjištění, jaké síly na ně působí, viz obr. 1.43.

Na základě uvolnění zapíšeme rovnice rovnováhy sil na obou tělesech:

V rovnici (1.32) vyjádříme jednotlivé síly a obdržíme soustavu dvou diferenciálních rovnic druhého řádu, které popisují chování těles:

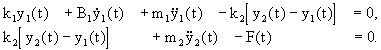
Z rovnice (1.33) opět vyjádříme druhé derivace polohy obou těles:

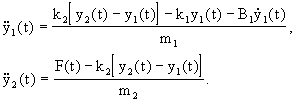
Řešení provedeme pro konkrétnínastavení parametrů m₁ = 2 kg, k₁ = 1 N m_-1, B₁ = 0,6 N s m_-1, m₂ = 1 kg, k₂ = 1,5 N m_-1, F = 10 N. Předpokládáme, že počáteční poloha obou těles je rovna nule. Pokud by tomu tak nebylo, provedeme posunutí počátku souřadnicového systému tělesa 2 do počátku souřadnicového systému tělesa 1. Na obr. 1.45 je znázorněn průběh polohy (plná čára) a rychlosti (čárkovaná čára) pohybu tělesa 2 a průběh polohy (čerchovaná čára) a rychlosti (tečkovaná čára) pohybu tělesa 2. Vidíme na něm, že tělesa jsou z počáteční klidové polohy uvedena do kmitavého tlumeného pohybu. Po jeho odeznění se poloha ustaluje na nových hodnotách. Srovnáním s předchozím příkladem pohybu samostatného tělesa zřetelně vidíme, jak se tělesa vzájemně ovlivňují.

Vzájemné ovlivňování těles je lépe patrné na grafech závislosti rychlosti na poloze. Na obr. 1.46 vidíme závislost rychlosti na poloze tělesa 2 a na obr. 1.47 graf závislosti rychlosti na poloze tělesa 1. Těleso 1 má větší hmotnost a současně působení na něj je tlumeno pohybem tělesa 2, proto je průběh závislosti bližší případu pohybu samostatného tělesa.

Závěr

Na předloženém příkladě jsme řešili pohyb soustavy dvou vázaných těles. Nyní můžeme soustavu doplnit dalšími tělesy, nebo zkoumat vliv působení síly s jiným průběhem. Např. vliv síly, jejíž hodnota má cyklický průběh, nejjednodušeji sinusový, ale také pulzní, pilový apod.

1.10. Literatura k simulaci základních pohybů těles

Analogový počítač TESLA AP-S ve školní praxi. Olomouc, UP 1969.
FARANA, R. 1993. Simulation program SIPRO 3.0 for IBM/PC. In Sborník mezinárodní konference CATE '93. Brno: Vojenská akademie, 27. - 29. 9. 1993, s. 457 - 460.
FARANA, R. 1992. Zkušenosti a poznatky z tvorby učebních textů s podporou výpočetní techniky. In Sborník přednášek konference "Pedagogický software 92". České Budějovice: Jihočeská univerzita, 8.-10. 6. 1992, s.62-63.
NOSKIEVIČ, P. 1992. Simulace systémů. Ostrava: ES VŠB, 1992.
NOVÁK, V. a ZíTEK, P. 1982. Praktické metody simulace dynamických systémů. Praha: SNTL/ALFA, 1982.
ONDRÁČEK, E. A JANíčEK, P. 1990. Výpočtové modely v technické praxi. Praha: SNTL, 1990.
SOUKUP, J. 1990. Identifikace soustav. Praha: SNTL, 1990.
STRÁNSKÝ, J. 1959. Vysokofrekvenční elektrotechnika II. Praha: ČSAV, 1959.
VEJRAŽKA, F. 1991. Signály a soustavy. Praha: ČVUT, 1991.
VITÁSEK, E.1987. Numerické metody. Praha: SNTL, 1987.
VÍTEČEK, A. a FARANA, R., aj. 1996. Univerzální simulační program SIPRO 3.4. Uživatelská příručka. Ostrava: KAKI Ostrava, 1996.
VÍTEČEK, A., aj. 1991. Počítačová podpora výukového procesu v oblasti automatizace. Simulační program SIPRO-VÝUKA. (Výzkumná zpráva). Ostrava: FS VŠB, 1991.
VÍTEČEK, A. a FARANA, R. a SMUTNÝ, L. 1992. Simulation Program SIPRO and Experience of its Application to the Teaching. In Sborník konference "CAE in ACT". Praha: ČVUT, květen 1992, s.17.-20.
ZÍTEK, P. 1990. Simulace dynamických systémů. Praha: SNTL, 1990.