Příklad 2.21
Telefonní ústředna zapojí během hodiny průměrně patnáct hovorů. Jaká je pravděpodobnost, že během čtyř minut zapojí: 1) právě jeden hovor, 2) alespoň jeden hovor, 3) alespoň dva a nejvíce pět hovorů [Hebák, P., Kalounová, J., 1978].
Řešení:
Střední hodnota pro 4 minuty: ![]()

Ústředna během čtyř minut zapojí právě jeden hovor s pravděpodobností 37 %, alespoň jeden hovor s pravděpodobností 26 %, alespoň dva a nejvíce pět hovorů s pravděpodobností 26 %.
Příklad 2.22
Znázorněme grafy
frekvenční funkce Poissonova rozložení pro l1 = 2, l2 = 5, l3
= 6, l4 = 10.
Tabulka 2.8 Hodnoty frekvenční funkce
|
k |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0,135 |
0,271 |
0,271 |
0,180 |
0,090 |
0,036 |
0,012 |
0,003 |
0,001 |
0,000 |
0,000 |
|
|
0,007 |
0,034 |
0,084 |
0,140 |
0,175 |
0,175 |
0,146 |
0,104 |
0,065 |
0,036 |
0,018 |
|
|
0,002 |
0,015 |
0,045 |
0,089 |
0,134 |
0,161 |
0,161 |
0,138 |
0,103 |
0,069 |
0,041 |
|
|
0,000 |
0,000 |
0,002 |
0,008 |
0,019 |
0,038 |
0,063 |
0,090 |
0,113 |
0,125 |
0,125 |
|
k |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
|
0,008 |
0,003 |
0,001 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
|
0,023 |
0,011 |
0,005 |
0,002 |
0,001 |
0,000 |
0,000 |
0,000 |
0,000 |
0,000 |
|
|
0,114 |
0,095 |
0,073 |
0,052 |
0,035 |
0,022 |
0,013 |
0,007 |
0,004 |
0,002 |
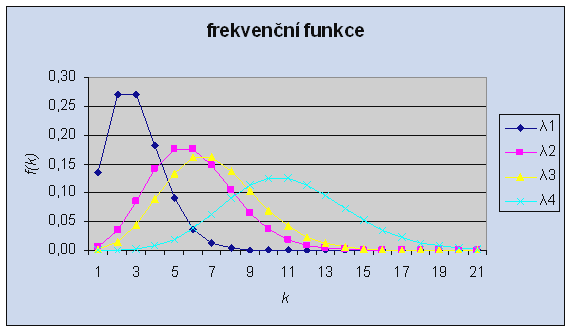
Obr. 2.22 Poissonovo rozdělení příklad 2.22
Protože je koeficient šikmosti větší než nula, jsou příslušné křivky asymetrické zprava.